Steer LLM Latents for Hallucination Detection

（ICML 2025）

Truthfulness Separator Vector = TSV

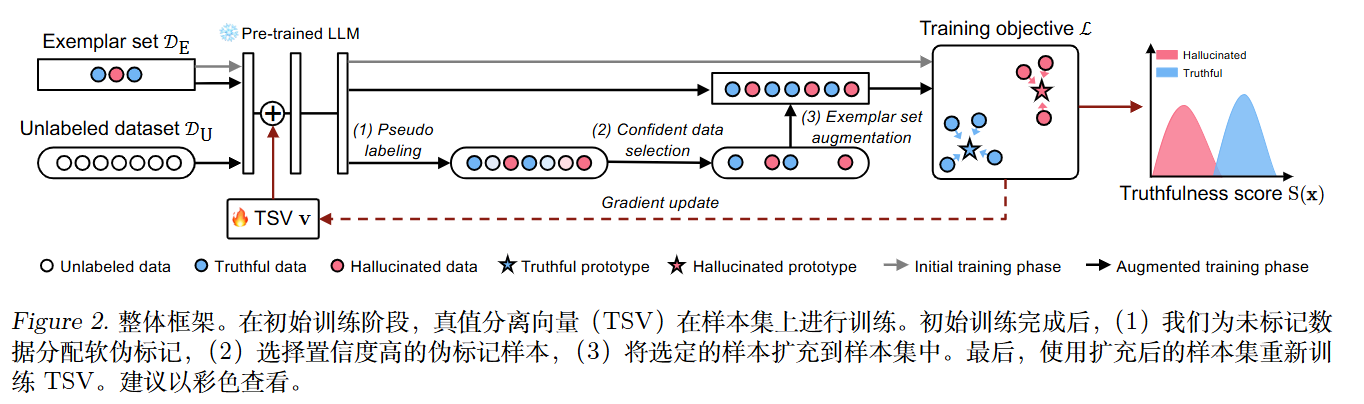
方法

依旧是$h=h+\lambda v$。但是不同于VTI等方法的v是真实-幻觉差分矩阵的SVD的v向量。

TSV采用了更复杂的方法，位置也不同。

第一阶段：基于MLE的有标签

TSV通过MLE来实现幻觉和真实空间的有效分离。
$$
argmax_v\Pi^{\mathcal{D}_E} _ {i=1} p(c_i\mid \Phi _ {final}(h_i^{(l)}+\lambda v))
$$
对于MLE，需要显式建模概率分布 $p(c_i\mid \Phi _ {final}(h_i^{(l)}+\lambda v))$。具体而言，使用具有单位范数的超球面分布来建模最终层的最后一个 token 嵌入，其中真实数据和幻觉数据各自形成不同的簇。

作者还扯到什么RMSNorm和Von Mises-Fisher 分布。

很ICML的风格。

类别条件概率表示为（其实就是softmax）：
$$
p(c\mid r^v)=\frac{exp(\kappa\mu_c^Tr^v)}{\sum _ {c’} exp(\kappa\mu _ {c’}^Tr^v)}
$$
其中$r^v=\Phi _ {final}(h^{(l)}+\lambda v)/||\Phi _ {final(h^{(l)}+\lambda v)}||_2$。$\mu_c$是类别c的类原型（Prototype Center），$\kappa \ge 0 $是控制分布围绕均值方向聚集紧密程度的集中参数$\mu_c$。

此时MLE相当于最小化负对数似然，这促使每一类内的嵌入紧密聚集在类中心附近：
$$
\mathcal{L}=-\frac{1}{|\mathcal{D}_E|}\sum _ {i=1}^{|\mathcal{D}_E|}\sum _ {c\in \mathcal{C}} q(c\mid r_i^v)logp(c\mid r_i^v)
$$
$q(\cdot\mid )$表示目标标签分

隔这在重温机器学习的内容呢

原型向量$\mu_c$可以通过指数移动平均更新。
$$
\mu_c \leftarrow norm[\alpha \mu_c+(1-\alpha)r^v]
$$
其中$r^v=\sum \frac{q(c\mid r_i^v)r_i^v}{\sum_j q(c\mid r_j^v)}$为类别c的规范化的嵌入的均值。

第二阶段：基于MLE的有标签

少量标注样本可能无法完全捕捉真实数据与幻觉数据分布中固有的多样性。为解决这一局限性，作者提出进一步引入未标记的训练数据以增强学习过程。

这部分使用的是最佳传输（OT）。

目标是找一个分配矩阵$Q\in R^{M\times 2}$，（M是无标注样本数），将M个样本分别给2个类别（真实/幻觉），同时最小化传输代价。

优化目标：

$$\min _ {Q} - \sum _ {m=1}^{M} \sum _ {c \in \mathcal{C}} Q _ {m,c} \log P _ {m,c} - \epsilon H(Q)$$

• $P _ {m,c}$：模型当前预测的概率（Cost Matrix 的反面）。
• $H(Q)$：熵正则项，用于平滑分配并允许使用快速的 Sinkhorn 算法求解。

约束条件：

1.每个样本的分配概率之和为1：$Q1_2=\frac{1}{M}1_M$,

2.类别平衡约束：$Q^T1_M=\omega$。这里的$\omega$是预期的类别分布向量（如[0.8,0.2]）。作者直接使用少量标注样本的类别比例作为$\omega$的估计。

利用 Sinkhorn-Knopp 算法迭代求解上述优化问题，得到最优的伪标签分布 $Q$。

OT 强制分配标签可能会给原本模糊的数据强加错误的标签。因此，作者计算每个样本的预测熵（不确定性）：

$$\Omega_i = - \sum _ {c} q(c|r_i^v) \log p(c|r_i^v)$$

只选择熵最小（最自信）的 $K$ 个样本加入到训练集 $\mathcal{D}_E$ 中。

将筛选出的高置信度无标注样本与原始标注样本合并，重复第一阶段的训练过程，进一步优化 $v$。

实验

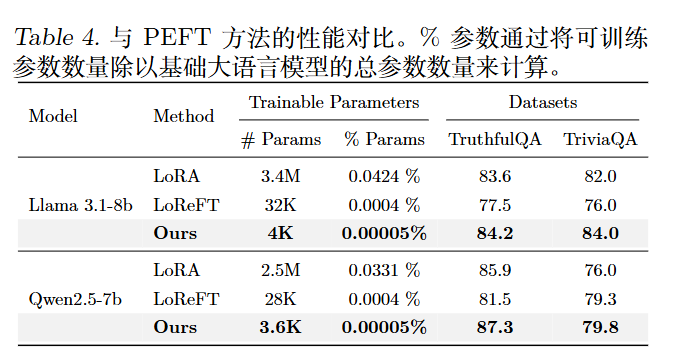
与 PEFT 方法的性能对比: