VASparse:通过视觉感知的 token 稀疏化实现高效视觉幻觉缓解
(CVPR 2025)
VASparse 提出了一种高效、即插即用的解码策略,在提升生成质量的同时保持甚至提升了推理速度。
Motivation & Observations
作者通过实证研究发现了 LVLMs 内部的三个关键现象:
1.注意力的高度稀疏性 (Sparse Activation)
LVLM 解码层的注意力机制呈现明显的长尾分布。仅保留前 1% 的高分 Token 就能恢复 98% 的注意力分数 。这意味着大部分 Token 在计算中是冗余的。
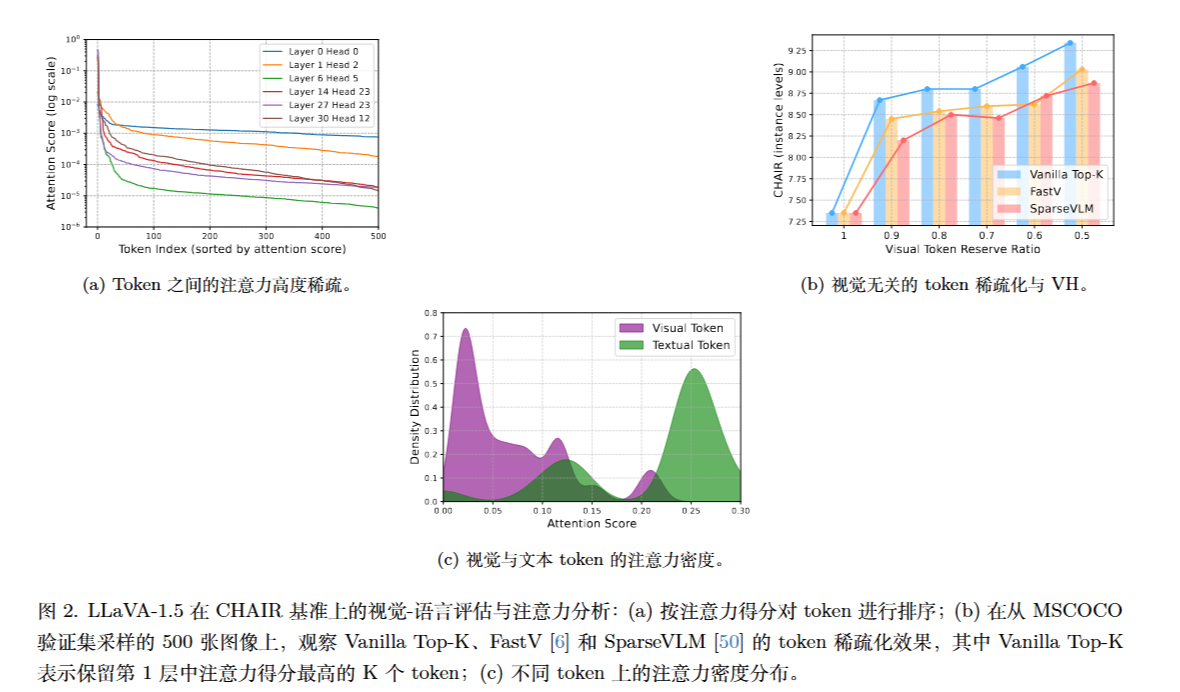
2.视觉无关的稀疏化会加剧幻觉
如果直接使用传统的 Token 稀疏化方法(如仅基于 Top-K 的剪枝),随着稀疏度增加,模型的幻觉反而会变严重。因为这种方法容易剪掉注意力分数较低但对图像理解至关重要的视觉。
3.注意力“下沉”现象 (Attention Sinking)
LVLMs 存在一种偏见,即大量的注意力会被分配给语义信息极低的文本 Token(如句号 . 或起始符 <s>),而忽略了图像 Token。这种“注意力下沉”导致模型过度依赖语言先验。
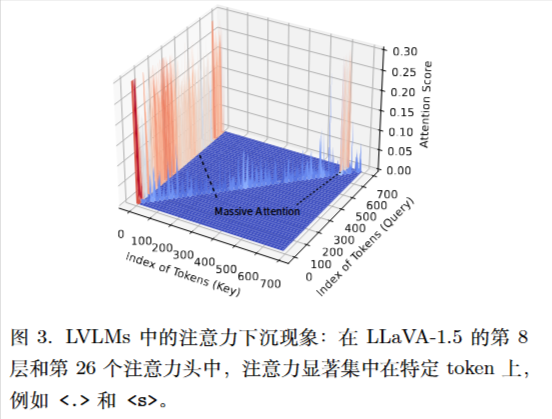
方法
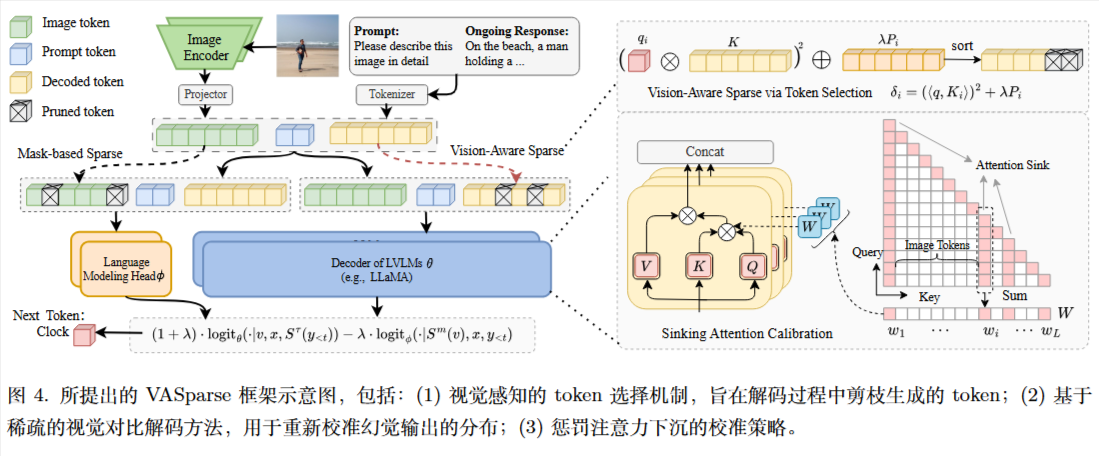
主要包含三个核心模块:
A. 视觉感知的 Token 选择 (Visual-Aware Token Selection)
为了解决直接剪枝导致的幻觉问题,作者设计了一种新的 Token 重要性评分标准 $\delta_i$ :
$$
\delta _ {i}=(\langle q,K _ {i}\rangle)^{2}+\lambda P _ {i}
$$
$\langle q,K _ {i}\rangle$: 原始的注意力分数。
$P_i$: 视觉显著性分数(Visual Saliency Score)。这是通过保留上一层注意力头中图像 Token 的权重计算得出的。
$$
P _ {i}=\frac{exp(\sum _ {k\in \mathcal{I}(v)}a _ {i,k})}{\sum _ {j}exp(\sum _ {k\in \mathcal{I}(v)}a _ {j,k})}
$$
其中:
$\mathcal{I}(v)$ 表示图像 Token 的集合。
$a _ {i,k}$ 表示 Token $i$ 与图像 Token $k$ 之间的注意力分数。
该公式本质上是计算当前 Token 对图像区域的总注意力,并进行归一化处理。
机制: 解码时根据 $\delta_i$ 排序,保留 Top-S 个 Token,从而强制保留关键的视觉信息。
B. 基于稀疏化的视觉对比解码 (Sparse-based Visual Contrastive Decoding, SVCD)
这是提高效率的关键。传统的对比解码通常需要运行两次完整的模型解码,非常耗时。VASparse 提出了一种轻量级策略:
- 原理: 直接将被掩盖视觉信息的 Token Embedding 输入到语言模型的解码头(Language Modeling Head)获取 Logits ($logit _ {\phi}$),跳过了繁重的解码器计算。
- 公式: 最终的输出概率分布为:
$$
y _ {t}\sim(1+\alpha)\cdot logit _ {\theta}(\cdot|v,x,S^{\tau}(y _ {<t})) - \alpha\cdot logit _ {\phi}(\cdot|S^{m}(v),x,y _ {<t})
$$
C. 注意力下沉惩罚 (Sinking Attention Penalty)
针对模型过度关注无意义文本 Token 的问题,引入动态惩罚矩阵 $W$ 。
- 通过累积注意力分数识别“下沉” Token,并在解码时重新校准权重:$(1+\beta)qK^{\top}-\beta W\odot qK^{\top}$。
理论
作者还证明了VASparse 的 Token 选择策略在数学上是全局最优的,而不仅仅是经验法则。
作者定义了一个联合优化问题,旨在最小化注意力恢复误差,同时最大化视觉感知权重。目标函数 $\mathcal{E}(M)$ 定义为:
$$
\min _ {M} \mathcal{E}(M) = \sum _ {i=1}^{L} (\langle q, K_i \rangle - M_i \langle q, K_i \rangle)^2 - \lambda P_i M_i
$$
- 约束:$\sum M_i = S$(稀疏度),$M_i \in {0, 1}$。
- 直觉:第一项希望保留原始注意力分数高的 Token(减少误差),第二项希望保留视觉显著性 $P_i$ 高的 Token(增加视觉感知)。
- 其中$\lambda$是用于平衡视觉感知与注意力召回率的权衡参数。
证明过程
令 $y_i = \langle q, K_i \rangle$。利用二值变量特性 $M_i^2 = M_i$ 和 $(1-M_i)^2 = 1-M_i$,将平方项展开并简化:
$$
\begin{aligned}
\mathcal{E}(M) &= \sum _ {i=1}^{L} [y_i^2 (1 - M_i)^2 - \lambda P_i M_i] \\
&= \sum _ {i=1}^{L} [y_i^2 (1 - M_i) - \lambda P_i M_i]
\end{aligned}
$$
进一步整理公式,分离常数项和含 $M_i$ 项:
$$
\mathcal{E}(M) = \underbrace{\sum _ {i=1}^{L} y_i^2} _ {\text{Constant}} - \sum _ {i=1}^{L} M_i (y_i^2 + \lambda P_i)
$$
要使误差 $\mathcal{E}(M)$ 最小,等价于使减号后面的求和项 最大。即求解:
$$
\max _ {M} \sum _ {i=1}^{L} M_i \underbrace{(y_i^2 + \lambda P_i)} _ {\delta_i}
$$
定义每个 Token 的边际收益为 $\delta_i = y_i^2 + \lambda P_i$。
这是一个经典的线性规划问题:在 $L$ 个物品中选择 $S$ 个以最大化总价值。
- 策略:按 $\delta_i$ 降序排列,取前 $S$ 个。
- 证明:假设存在一个更优解 $M$ 包含了一个低分 Token $j$ 而放弃了一个高分 Token $i$(即 $\delta_i > \delta_j$)。如果我们交换它们(选 $i$ 弃 $j$),总收益将增加 $\delta_i - \delta_j > 0$。
- 结论:因此,VASparse 提出的基于 $\delta_i$ 排序的 Top-S 策略是该优化问题的全局最优解。