Do Not Merge My Model! Safeguarding Open-Source LLMs Against Unauthorized Model Merging
(AAAI 2026)
创新性很强,理论性很强的一篇论文。是不是可以拿个Oral。
问题定义
模型合并 (Model Merging) 本身是一种有用的技术。研究人员可以将多个“专家模型”(例如,一个擅长编码,一个擅长数学)合并成一个更强大的通用模型,而无需重新训练 。
威胁的产生:这种技术的出现也带来了一个新的威胁,论文称之为 “模型合并窃取” (model merging stealing) 。
具体场景:许多模型(例如在 Hugging Face 上)虽然开源,但是基于限制性许可证(如 CC BY-NC-ND)发布的,明确禁止商业用途 。然而,“搭便车者” (free-riders) 可以下载这些受保护的专家模型,将它们与自己的模型非法合并,从而低成本地获取受保护模型的能力用于商业牟利 。
窃取为何严重:这种窃取行为非常隐蔽,易于执行,且难以追查 。更糟糕的是,研究表明,模型合并过程可能会使传统的水印技术失效 ,导致模型所有者无法证明其知识产权被盗用。
现有方法局限性
论文指出,现有的模型保护方法无法同时满足三个关键属性 :
- 主动性 (Proactivity):传统方法如水印 和指纹 都是“被动防御”,只能在模型被盗之后尝试进行验证 。它们无法阻止合并行为的发生。
- 兼容性 (Compatibility):一些主动防御(如基于 TEE 硬件或加密密钥的授权系统 )需要额外的组件或专门的硬件支持,这在开放源码环境中是不现实的 。
- 安全性与实用性 (Security with Utility):另一些兼容性方法(如发布“仿真器”模型)往往难以平衡安全性和模型性能。简化的仿真器会牺牲太多性能 ,而精确的仿真器又容易泄露模型权重,不够安全 。
方法
核心思想: MergeBarrier 的基本思路是,成功的模型合并要求各个专家模型位于同一个低损失盆地内,从而形成一条线性路径,其中所有中间点(作为合并后的模型)均处于低损失盆地内并保持高性能。为阻止模型合并,我们对原始模型的权重进行变换,将
其移出原有的损失盆地,从而消除低损失线性路径,导致合并后模型性能下降。
MergeBarrier 将核心思想应用于注意力权重的投影以及前馈网络(FFN)权重的重参数化,同时保持模型原有的性能。
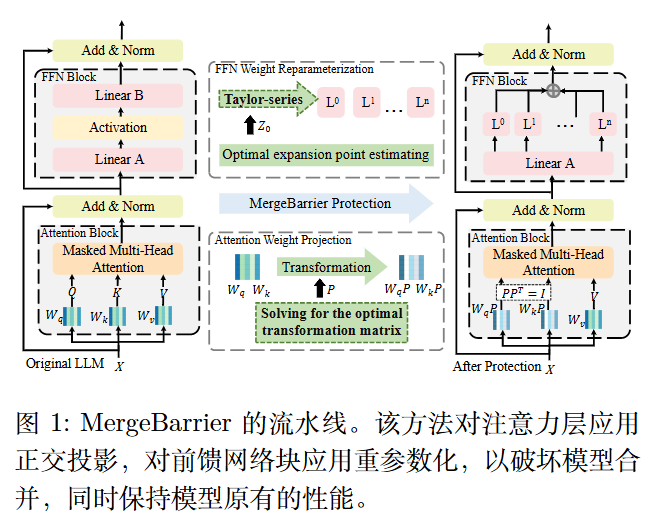
注意力权重投影
若$PP^T=I$,则
$$
\begin{align}
O&=softmax(\frac{XW_qPP^TW_k^TX^T}{\sqrt c})XW_v
\\
&=softmax(\frac{XW_qW_k^TX^T}{\sqrt c})XW_v
\end{align}
$$
为了确保合并后的模型被推出原始的低损失盆地,我们旨在寻找一个正交矩阵 P ,使其与该盆地的距离最大化。
即
$$
max_P \frac{1}{16}||(W_qP+W_q)(W_kP+W_k)^T-(W_q+W_q)(W_k+W_k)^T||_F^2
$$
有定理:
Theorem 2. (a) 最大化式 (2) 足以最大化 $||W_q(P-I)||_F^2 + ||W_k(P-I)||_F^2$。
(b) 若 $\lambda_i > 0$,则 $(U^\top PU) _ {ii} = -1$;若 $\lambda_i < 0$,则 $(U^\top PU) _ {ii} = 1$。
(c) 若 $\lambda_i = 0$,则 $(U^\top PU) _ {ii}$ 可取任意值。
理想情况下,最大扰动发生在 $P = -I$ 时,此时所有方向均反转,距离达到最大,但这会暴露真实模型权重。
为解决此问题,作者采用一种松弛方法:对前-k 个特征方向 (即具有最大 $\lambda$ 值的方向) 设置 $(U^\top PU) _ {ii} = -1$,其余方向设置 1。通过应用逆变换,得到满足所需条件的 $P$。
FFN权重重参数化
FFN 层的计算通常是 Linear -> Activation -> Linear。该方法针对的是第二个线性层及其前面的激活函数 。
将这个激活函数在某个“展开点” $z_0$ 进行泰勒级数展开。
对于一个 FFN块,令 W 和 c 分别表示第二层线性层的权重和偏置。
该层的输出记为 $y$。我们使用泰勒级数对其进行重新参数化,如下所示:
$$
\begin{align}
y - c & \\
& = (y_1, \dots, y_n) - (c_1, \dots, c_n) \\
& = (W_1 \odot Act(z + b), W_2 \odot Act(z + b), \dots, W_n \odot Act(z + b)) \\
& \approx (W_1 \odot \sum _ {n=0}^{N} \frac{Act^{(n)}(z_0 + b)}{n!}, \dots, W_n \odot \sum _ {n=0}^{N} \frac{Act^{(n)}(z_0 + b)}{n!}) \\
& = W \frac{Act^{(0)}(z_0 + b)}{0!} (z_0 - z)^0 + \dots + W \frac{Act^{(N)}(z_0 + b)}{N!} (z_0 - z)^N \\
& = \hat{W}^0 (z_0 - z)^0 + \dots + \hat{W}^N (z_0 - z)^N
\end{align}
$$
此处,$W_i$ 为 $W$ 的第 $i$ 列。$z$ 为带有偏置 $b$ 的第一层线性层的输出。扩展点 $z_0$ 设置为集合 $Z$ 中 $z _ {max}$ 与 $z _ {min}$ 之间的中点,该集合由训练样本的特征表示 $z$ 构建而成。符号 $\odot$ 表示逐元素乘法。
同时,该方法并不仅限于泰勒展开——也可采用其他基函数,如埃尔米特多项式。
另外,泰勒展开(以及计算机的浮点数)总会存在一个极小的“余项误差” 。这个微小的、类似噪声的误差,反而成为了最强的安全保障 。如果攻击者试图通过解方程,从发布的多项式系数 $\hat{W}$ 反向破解出原始权重 $W$,这个求解问题会因为“余项误差”的存在,转变为一个“带误差学习”(Learning With Errors, LWE)问题。