模型后面的层是否无用？

大模型的扩展始终强调深度增加，实证证据表明模型性能随着层数增加而提高——尽管收益递减。早年的深度学习也强调深度比宽度更重要，且深度能提高模型性能。

但是也有不少文章（比如博客之前写过的一些）指出，后面的层会扼杀模型原有的能力。

模型后面的层究竟执行什么样的任务？

这次进行四篇论文的串读。一篇ICLR2025，一篇NIPS workshop，两篇arxiv。

什么因素影响LLM的有效深度?

（NIPS workshop）《What Affects the Effective Depth of Large Language Models?》

分析对象： 研究了Qwen-2.5模型家族（从1.5B到32B）

分析技术： 使用了多种前沿的“可解释性”技术来探测模型每层的行为，包括

残差余弦相似度 (residual cosine similarity)

Logit透镜 (logit lens)

层跳过效应 (layer skipping)

残差擦除 (residual erasure) ：通过用无信息的基线替换其残差向量

积分梯度 (integrated gradients) 。该指标将模型的预测结果分配到每个答案token上，并归因于每一层的贡献。计算所有答案token的输出logits相对于每一层和每个token位置的激活值的梯度。

引入两种定量指标来比较不同模型和数据集的有效深度。

对于残差余弦相似度，将各层、MLP和SelfAttention模块的相似度分数进行平均，并将有效深度识别为平均相似度从负转正的点。

对于logit镜头，使用两个指标：我们将有效深度定义为KL散度从最终输出下降到其最大观测值一半以下的层，或者定义为top‑5 token与最终输出首次超过0.3的层。

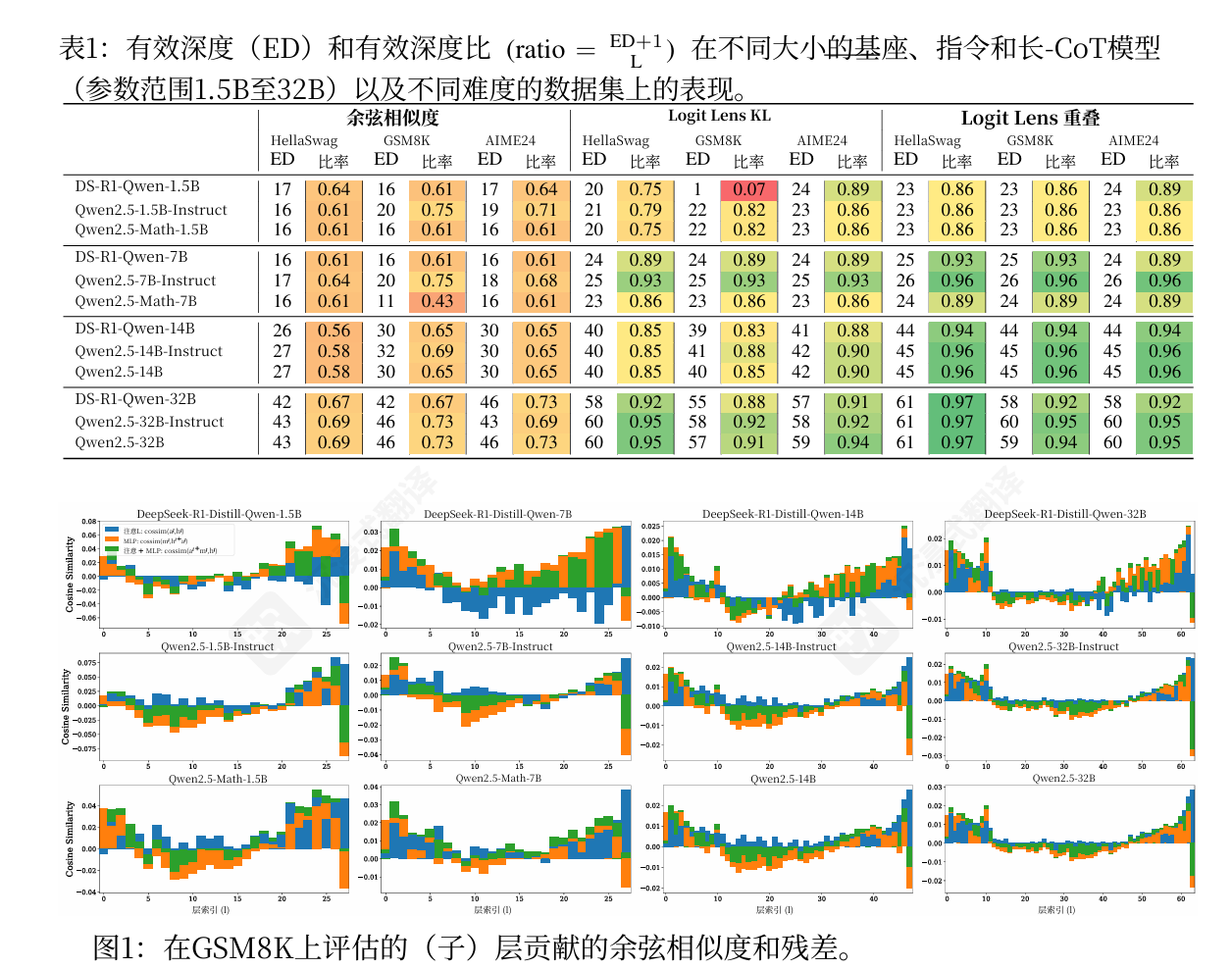
关键发现：

规模的影响： 模型的“有效深度”确实随模型规模的增大而增加，但有效深度占总深度的比例却保持稳定 。这意味着，更大的模型只是在复制相同的层利用模式，而不是更深入地使用其层级。模型计算存在一个明显的“相变”：早期层负责特征组合，而后期层（占了很大比例）仅在进行微小的调整。
训练类型的影响： 研究者们本以为用于复杂推理的Long-CoT模型会“思考得更深” ，但结果令人惊讶：Long-CoT模型的有效深度与基础模型相比没有显著增加 。其推理能力的提升，很可能来自处理更长上下文的能力，而不是更深的单令牌（per-token）计算。
任务难度的影响： 同样反直觉的是，模型的有效深度在所有不同难度的任务上都基本保持一致 。模型并不会因为问题更难（例如从常识问答到高中数学竞赛）就动态地使用更多的层。

LLM如何使用它们的深度?

（arxiv 10月）《How Do LLMs USE THEIR DEPΤΗ?》

分析工具：使用TunedLens（一种改进的Logit透镜），它能更准确地将模型的中间层隐藏状态解码为词汇表的概率分布。
$$
TunedLens(h^l)=LogitLens(A_lh^l+b_l)
$$
TunedLens探测器被训练以最小化最终层概率分布与中间层概率分布之间的 KL 散度：
$$
argmin_{A_l,b_l}\quad E[D_{KL}(f_\theta(h^l)||TuneLens(h_l))]
$$
根据每个模型的词表 token 在语料库中出现的频率将其划分为四个桶

(i) Top1-10桶，包含语料库中前 10 个最频繁的 token，约占语料库的 23-25%，具体比例因模型而异

(ii) Top11-100 桶，包含接下来的 90 个最频繁的 token，约占语料库 token 的 16-20%

(iii)Top101-1000 桶，包含接下来的 900 个最频繁的 token，约占语料库 token 的 16-21%

(iv) Top1000+ 桶，包含其余的 token，约占语料库的 35-40%

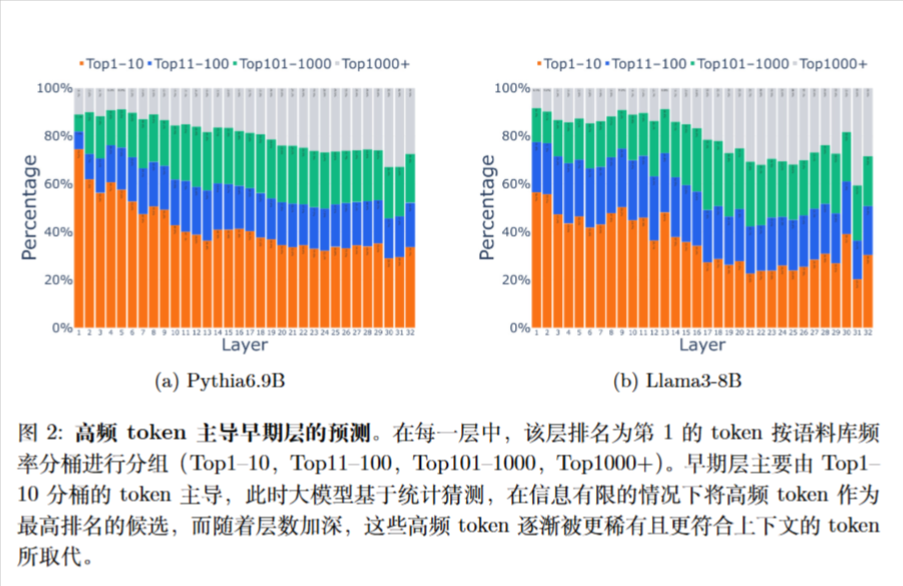
大语言模型通过在早期层中将最频繁的 token 提升为最高秩的候选，来进行统计猜测。随着上下文信息在模型中不断深入，这些基于语料库统计的猜测逐渐被修正为适当的预测，此时低频 token 开始出现。

作者表明大模型是天然的动态深度模型，能够灵活利用其深度：在较浅的层次上执行较简单的任务（或子任务），而将更复杂的任务留到后续层完成。

作者还发现简单的、高频的功能词（如”the”）在浅层到中层就会被模型锁定。而复杂的、信息量大的内容词（名词、动词）需要到更深的层才能被最终确定。

多项选择： 这是一个清晰的两阶段过程。阶段一（模型前半段）： 模型识别出所有有效的选项（如A, B, C, D），并将它们提升到高排名。阶段二（模型后半段）： 模型在这些有效选项之间进行权衡与推理，最终确定答案。

以上被称为“复杂度感知的深度使用”。

深层网络的惊人无效性

（ICLR 2025）《The Unreasonable Ineffectiveness of the Deeper Layers》

该篇论文也关注LLM的深度利用问题，但它采取了更激进的“破坏性”实验方法——层剪枝 (Layer Pruning)。

论文假设，如果一个层块的输入和输出表征非常相似（即这个块没做什么有意义的工作），那么它就可以被移除。他们计算输入和输出之间的“角距离” (angular distance) ，并剪掉距离最小（最相似）的那个块。

角距离为：
$$
d=\frac{1}{\pi}arccos\left(\frac{x^{(l)}\cdot x^{(l+n)}}{||x^{(l)}||\cdot|| x^{(l+n)}||}\right)
$$

简单启发式策略： 他们发现，越深的层，其表征与其相邻层越相似。因此，他们尝试了一种更简单的策略：直接移除最后面的n层（保留最后一层LM head）。

剪枝会破坏层与层之间的连接，可能损害模型太多性能了，故作者使用QLoRA在通用数据集（C4）上进行少量微调，以“治愈”这种损伤。

实验结果

在MMLU和BoolQ等知识问答基准上，Llama-2-70B的表现惊人地稳健。高达40-50%的层被移除后，模型的准确率几乎没有下降 。一旦超过这个临界点，性能会突然“崩溃”到随机猜测的水平。

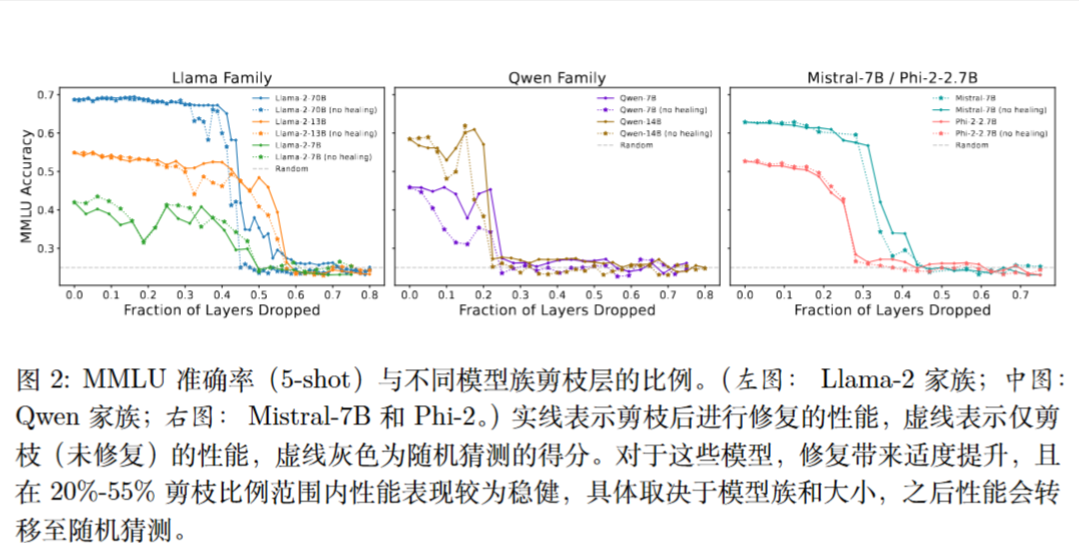
作者还考察了层剪枝对预训练最优化目标的影响，即在 C4 验证数据集的一个子集上评估的下一个 token 预测的交叉熵损失。

为了在具有不同词汇表大小的模型之间进行公平比较 V ，作者通过 log V 归一化损失，这对应于以均匀概率随机采样 token 时的损失。

也有相似的骤变现象，但是“治愈”操作可以修复。

表示之间的角距离

作者发现两点：

(i) 最小的距离出现在更深的块中，这意味着深层通常彼此非常相似，可以更容易地被丢弃

(ii) 最深的块——包含最后一层的块——之间的距离取极大值或接近极大值，这意味着永远不应丢弃最后一层。

不过也有一些例外，对于某些模型，例如 Phi-2-2.7B，或者某些模型中的最大块，例如 Llama-2-7B，最后的少数层似乎很重要。

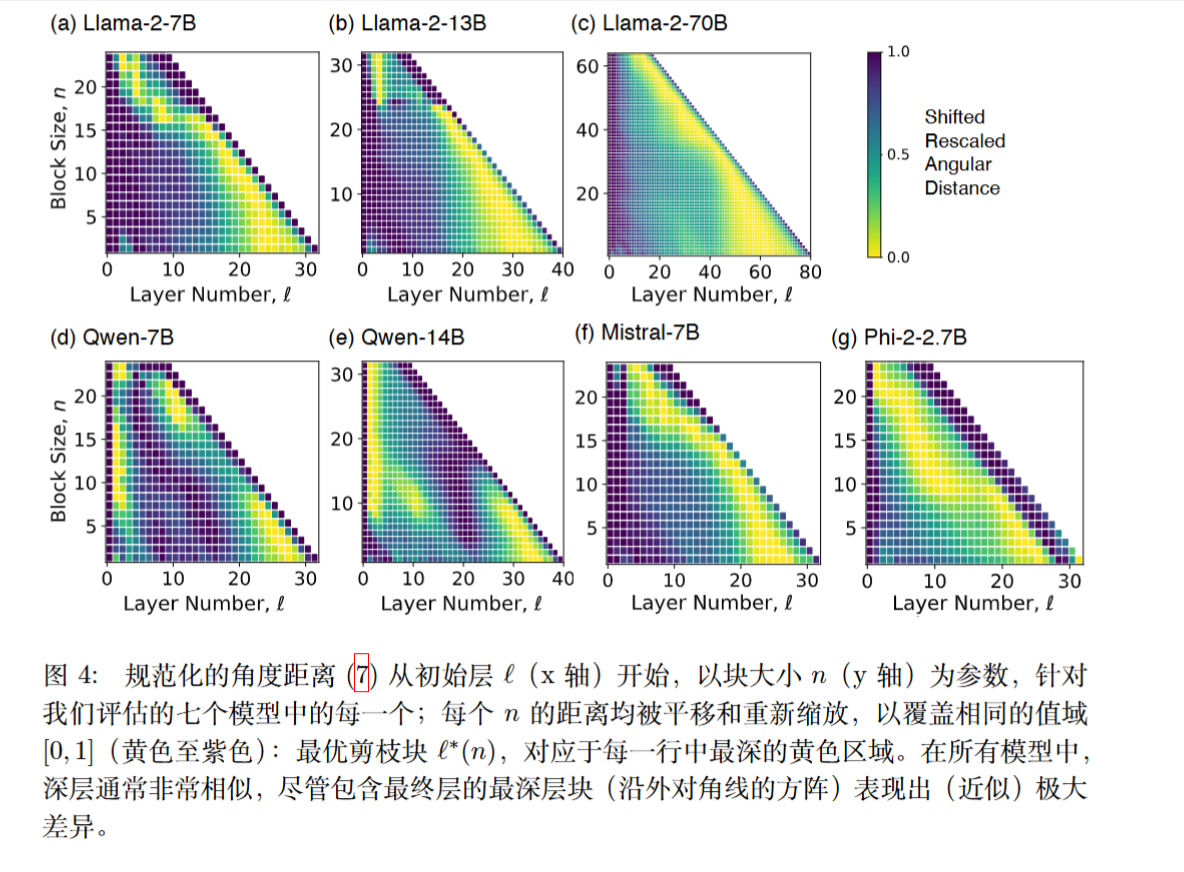
直接移除最后面的n层

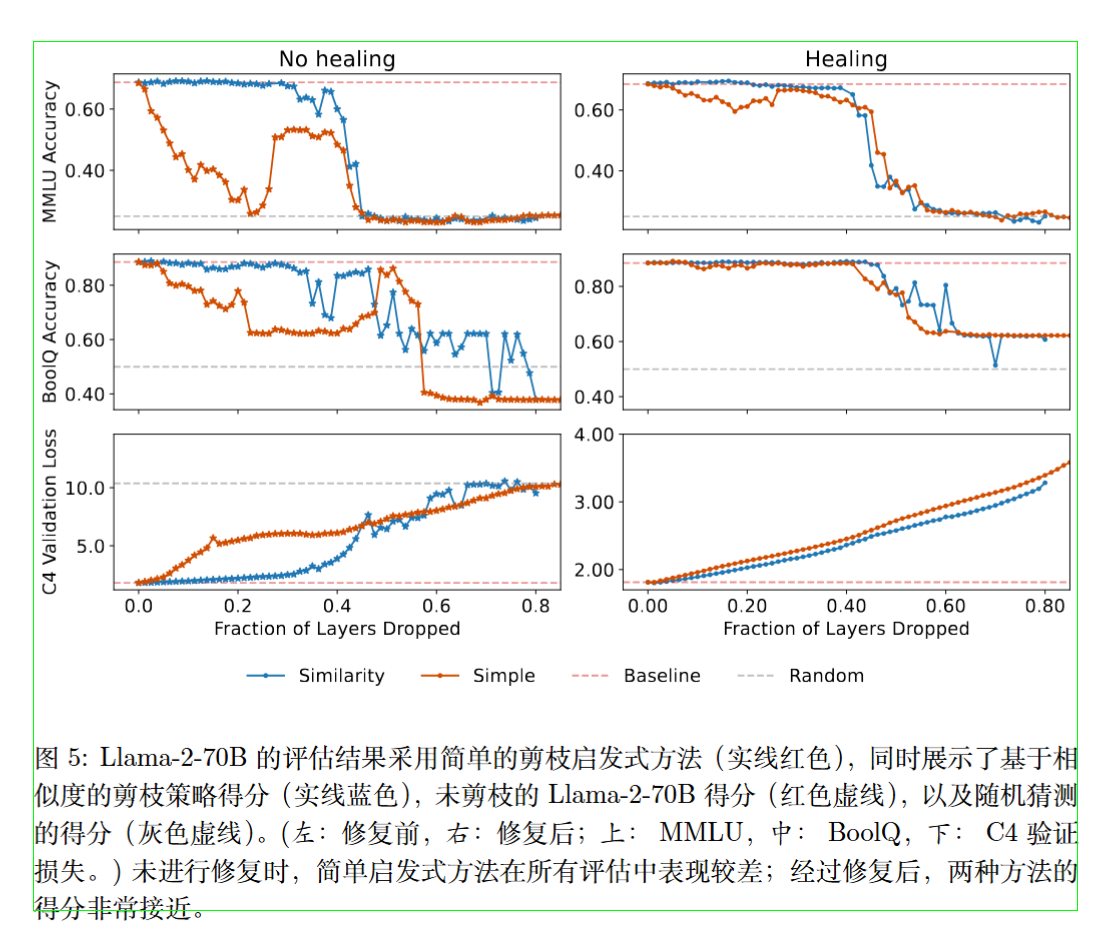
经过“治愈”后，简单的“移除最深层”策略，其效果与复杂的“相似度”策略几乎一样好 。这强有力地证明了，最深的那些层是“最不重要”的。

DR.LLM: LLM中的动态层路由

《DR.LLM: DYNAMIC LAYER ROUTING IN LLMS》

DR.LLM保持预训练LLM的权重完全冻结。它只为每一层额外添加一个极轻量的“路由器” (Router) 。

在推理时，每一层的路由器会检查当前的隐藏状态，然后做出三个决策之一：跳过 (Skip) 当前层，执行 (Execute) 当前层，或重复 (Repeat) 当前层（即再执行一次）。

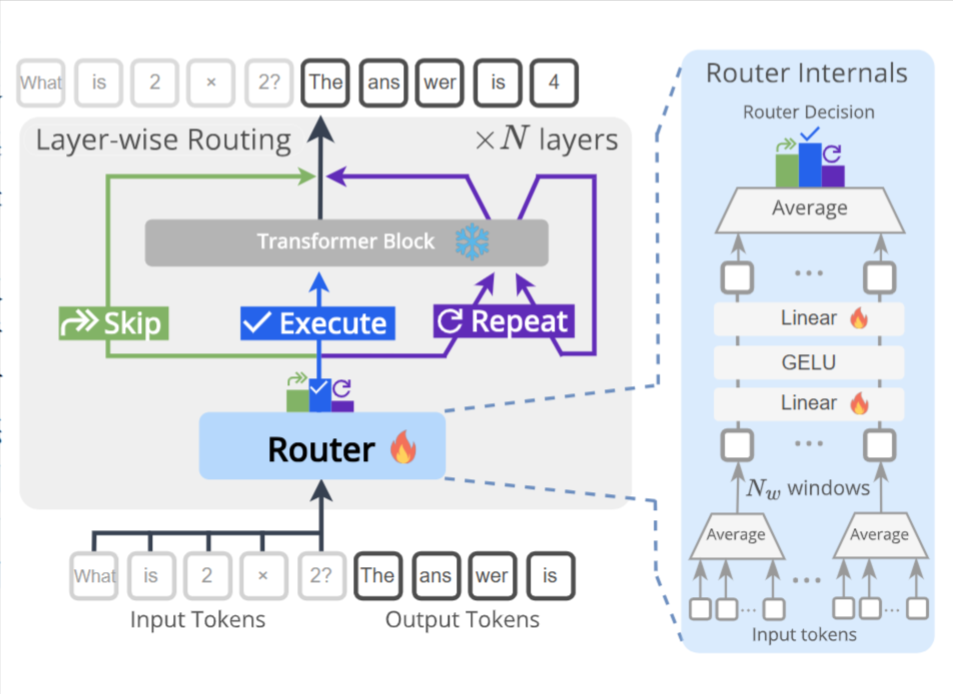
训练过程

作者首先使用蒙特卡洛树搜索 (MCTS)，在训练数据上（如ARC和DART）为每个样本搜索“最优执行路径” 。MCTS的目标是找到在一定计算预算下，能使准确率最大化（或保持不变）的路径组合（例如：[执行, …, 跳过, …, 重复, …]）。

作者使用这个MCTS找到的4000个“最优路径”作为标签，通过监督学习的方式来训练那些轻量级的路由器，使其学会模仿MCTS的决策。

路由器使用窗口池化 (windowed pooling) 来高效处理长序列，并使用Focal Loss来解决决策标签极度不平衡的问题（因为“执行”远多于“跳过”和“重复”）。
$$
\alpha_c = \frac{1 - \beta}{1 - \beta^{n_c}} / \frac{1}{3} \sum_{c’} \frac{1 - \beta}{1 - \beta^{n_{c’}}}, \quad \mathcal{L} = -\frac{1}{L} \sum_{\ell=1}^L \alpha_{y_\ell^\ast} (1 - p_{\ell, y_\ell^\ast})^\gamma \log p_{\ell, y_\ell^\ast}
$$

默认使用$\gamma=2,\beta=0.999$.

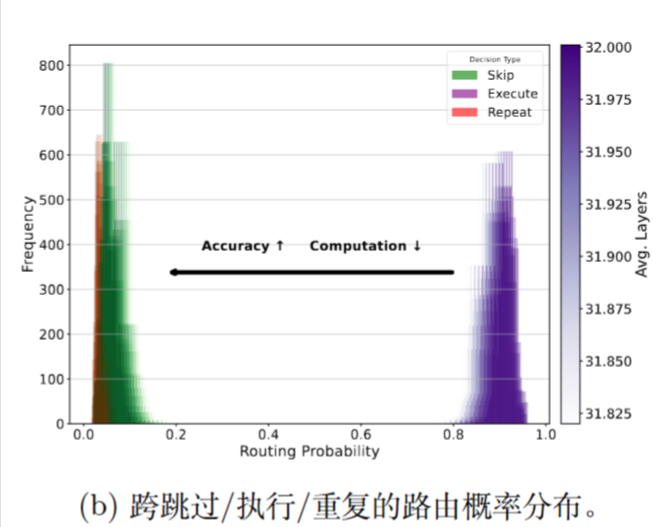
实验

红色 (值>1) 表示该层倾向于被“重复”；蓝色 (值<1) 表示倾向于被“跳过”；接近白色的浅蓝 (值≈1) 表示被“执行”。

作者指出，这与先前的论文相似，模型在早期层保持稳定，在中期层节省算力（跳过），并在晚期层（尤其是在困难任务上）投入额外算力（重复） 。

也许我是色盲，我好像并没有看到红色。