幻觉与越狱的一致性
(ICLR 2026在投)
原标题是《从幻觉到越狱:重新思考大型基础模型的脆弱性》
作者提出一个统一的理论框架,将越狱行为建模为 token 级别的最优化,将幻觉现象建模为注意力级别的最优化。
在此框架下,作者建立了两个关键命题:
(1) 相似损失收敛——在优化目标特定输出时,两种漏洞的损失函数表现出相似的收敛特性
(2) 注意力重分配中的梯度一致性——两者均表现出由共享注意力动态驱动的一致梯度行为。
引言
幻觉,即模型生成的内容偏离事实准确性。
越狱,即攻击者操纵模型行为以绕过安全约束。
令人惊讶的是,我们观察到这两种失败不仅相互关联,而且在实践中彼此影响。应用一种逃逸防御提示可以缓解视觉推理任务中的幻觉现象,使模型如 LLaVA-1.5和 MiniGPT-4能够正确判断视觉错觉。反之,引入一种幻觉缓解策略可能导致模型拒绝此前有效的逃逸提示。这种双向效应表明存在一个共享的潜在机制,挑战了幻觉与逃逸源于独立原因的传统观点。

初步建模
建模越狱
使用统一的输入表示来建模大模型(LLMs)和视觉-语言模型(VLMs)上的越狱攻击。今 $x^t$ 表示文本输入,其被编码为文本嵌入 $\mathbf{H}^t _ {1:n}$。如果模型为多模态,则视觉输入 $x^v$ 通过特征提取器 $g$ 处理,并投影到语言空间以生成视觉嵌入 $\mathbf{H}^v _ {1:l} = W \cdot g(x^v)$。完整的输入表示为 $[\mathbf{H}^v _ {1:l}; \mathbf{H}^t _ {1:n}]$;对于单模态 LLMs,这简化为 $[\mathbf{H}^t _ {1:n}]$。
模型生成输出序列 $\mathbf{y}$ 的概率为:
$$
p(\mathbf{y} \mid \mathbf{H}^v _ {1:l}, \mathbf{H}^t _ {1:n}) = \prod _ {i=1} p(y_i \mid \mathbf{y} _ {1:i-1}, [\mathbf{H}^v _ {1:l}, \mathbf{H}^t _ {1:n}])
$$
在对齐的 LFM 中,输出行为由一个潜在的奖励模型 $R^*$ 间接塑造,该模型反映了与人类偏好的对齐程度。越狱攻击旨在通过将一个良性输入 $[\mathbf{H}^v _ {1:l}; \mathbf{H}^t _ {1:n}]$ 扰动为对抗性输入 $[\mathbf{\tilde{H}}^v _ {1:l}; \mathbf{\tilde{H}}^t _ {1:n}]$,从而诱导模型生成低奖励或有害的输出:
$$
\mathbf{y}^* = \min R^* (\mathbf{y} \mid [\mathbf{\tilde{H}}^v _ {1:l}, \mathbf{\tilde{H}}^t _ {1:n}])
$$
不直接访问 $R^\ast$,我们优化对抗输出 $\mathbf{y}^\ast$ 的似然,将越狱损失定义为:
$$
\mathcal{L}^{adv}([\mathbf{\tilde{H}}^v _ {1:l}; \mathbf{\tilde{H}}^t _ {1:n}]) = -\log p(\mathbf{y}^* \mid [\mathbf{\tilde{H}}^v _ {1:l}, \mathbf{\tilde{H}}^t _ {1:n}])
$$
通过在约束扰动集 $\mathcal{A}$ 上最小化该目标,获得最优对抗嵌入:
$$
[\mathbf{\tilde{H}}^v _ {1:k}; \mathbf{\tilde{H}}^t _ {1:n}] = \underset{[\mathbf{\tilde{H}}^v _ {1:k}; \mathbf{\tilde{H}}^t _ {1:n}] \in \mathcal{A}([\mathbf{H}^v _ {1:k}; \mathbf{H}^t _ {1:n}])}{\arg \min} \mathcal{L}^{adv}([\mathbf{\tilde{H}}^v _ {1:k}; \mathbf{\tilde{H}}^t _ {1:n}])
$$
该公式捕捉了攻击者的意图:通过在嵌入层面施加扰动,将模型输出分布推向不安全的补全结果,这在白盒和黑盒越狱文献中是一种常见情景。
建模幻觉
作者将幻觉建模为注意力级别的扰动,这些扰动会错误地分配输入序列中的关注点。考虑输入嵌入 $[\mathbf{H}^v _ {1:l}; \mathbf{H}^t _ {1:n}]$ 位于一个 $d_e$ 维空间中。
为简化分析,只研究单个注意力块 ,其中注意力权重 $A _ {ij}$ 与输出嵌入 $o_i$ 的计算方式如下:
$$
A _ {ij} = \frac{\exp \left((W_Q \mathbf{H}_i)^T (W_K \mathbf{H}_j)\right)}{\sum _ {k=1}^{n+l} \exp \left((W_Q \mathbf{H}_i)^T (W_K \mathbf{H}_k)\right)}
$$
$$
o_i = \sum _ {j=1}^{n+l} A _ {ij} \cdot (W_V \mathbf{H}_j)
$$
其中 $W_Q$、$W_K$ 和 $W_V$ 是投影矩阵。幻觉发生在注意力分配错误时,这会降低对相关区域的关注,同时增加对语义无关 token 的关注。
为了模拟这种行为,向输入嵌入添加扰动向量 $\Delta^t$ 和 $\Delta^v$:
$$
\mathbf{\tilde{H}}^t _ {1:n} = \mathbf{H}^t _ {1:n} + \Delta^t, \quad \mathbf{\tilde{H}}^v _ {1:k} = \mathbf{H}^v _ {1:k} + \Delta^v
$$
扰动后的嵌入 $[\mathbf{\tilde{H}}^v _ {1:l}; \mathbf{\tilde{H}}^t _ {1:n}]$ 导致更新的注意力得分:
$$
A^\Delta _ {ij} = \frac{\exp \left((W_Q \mathbf{\tilde{H}}_i)^T (W_K \mathbf{\tilde{H}}_j)\right)}{\sum _ {k=1}^{n+l} \exp \left((W_Q \mathbf{\tilde{H}}_i)^T (W_K \mathbf{\tilde{H}}_k)\right)}
$$
以及对应的输出嵌入 $\tilde{o}_i = \sum _ {j=1}^{n+l} A^\Delta _ {ij} \cdot (W_V \mathbf{\tilde{H}}_j)$。
我们定义一个幻觉损失,以引导注意力集中在目标位置 $t$,同时最小化对非目标区域的注意力:
$$
\mathcal{L}^{hallu} = \sum _ {i=1}^m \left( -\log \left( A^\Delta _ {it} \right) + \lambda \sum _ {j \neq t} \log \left( A^\Delta _ {ij} \right) \right)
$$
其中 $m$ 为输出 token 的数量,$\lambda$ 用于平衡关注与抑制。该损失函数将幻觉可被建模并通过对注意力重新分配进行结构化约束来缓解的概念具体化。
命题
作者假设了两个命题,并通过实验证明了它们的可靠性。
对于幻觉最优化,作者通过定义一个固定的注意力目标位置,最大化注意力重分配损失 。
对于越狱攻击,作者实现了 GCG 方法 ,该方法通过迭代地在提示词后附加一个可训练后缀,以提高预定义对抗性目标输出的似然。后缀初始化为 20 个感叹号序列。
为了隔离文本模态的优化行为,并确保在不同情景下进行公平比较,所有基于梯度的实验中禁用视觉输入。
相似的损失收敛
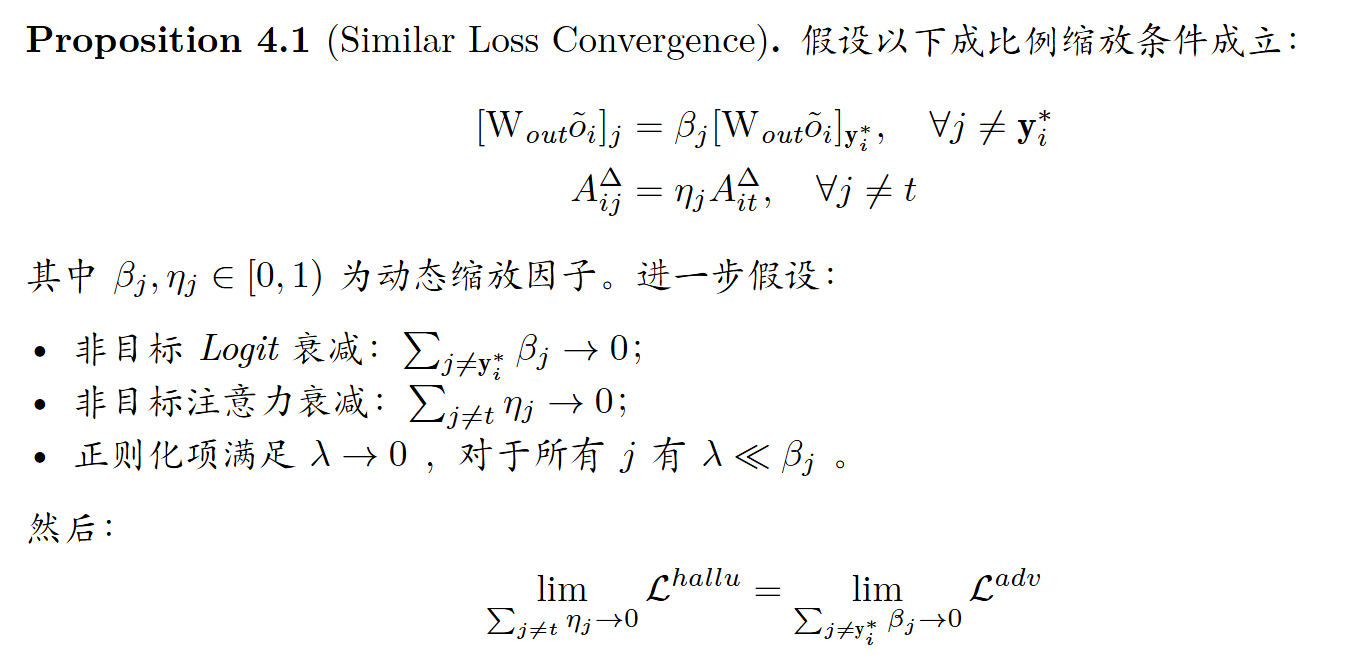
实验
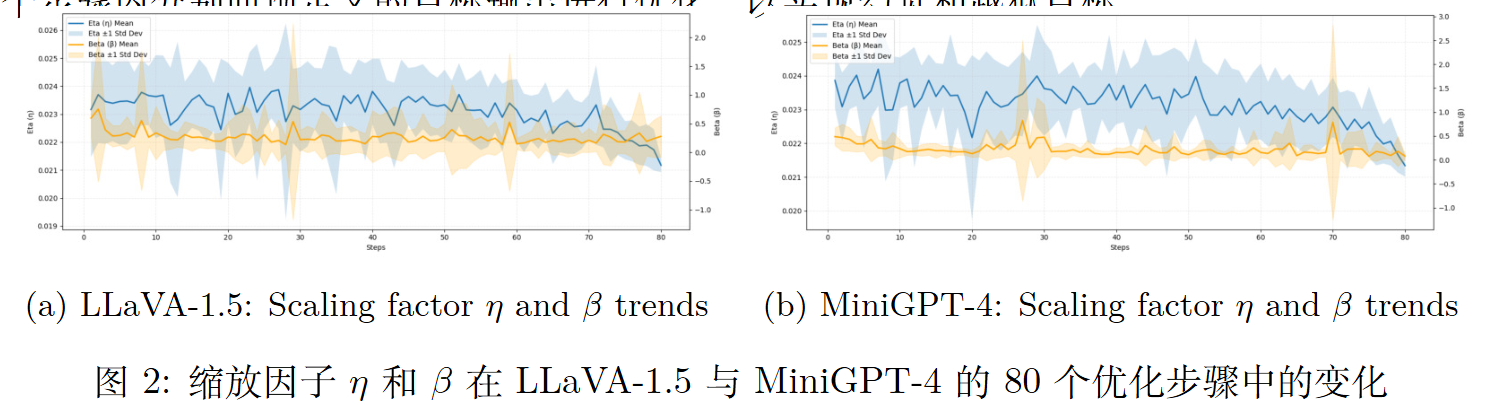
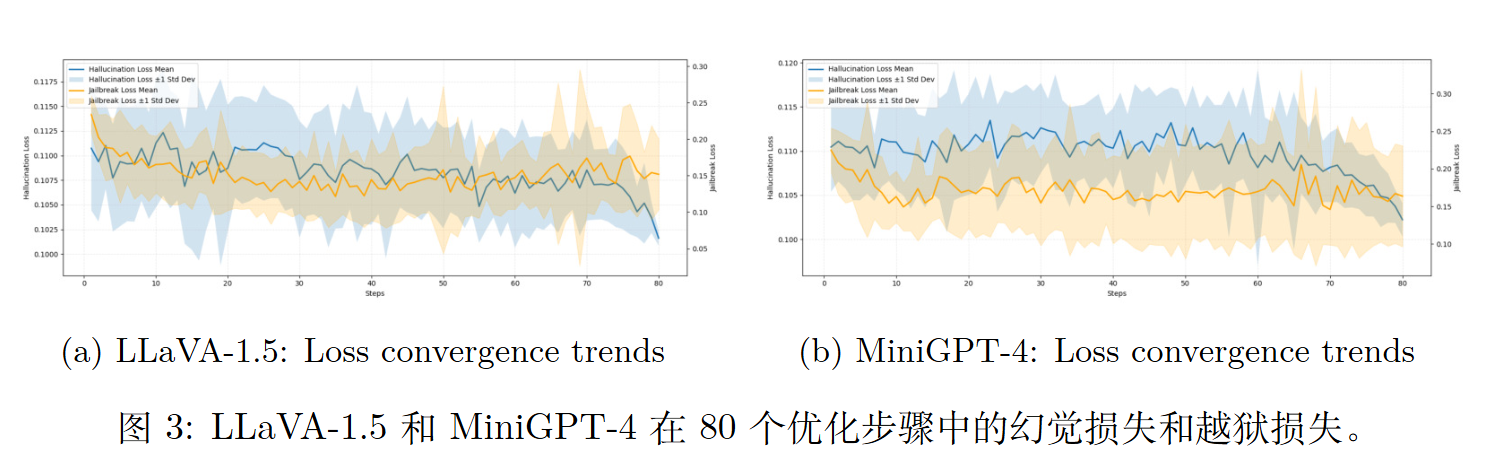
注意力重新分配中的梯度一致性

这意味着,无论是为了诱导幻觉还是为了实现越狱,对模型输入(嵌入)的扰动,都会在嵌入空间中沿着相似的方向推动模型 。换句话说,影响一个漏洞的扰动很可能也会影响另一个 。

跨现象缓解:在幻觉与越狱攻击之间泛化防御策略
幻觉和越狱攻击具有相似的最优化结构和梯度行为。
故针对一种漏洞开发的缓解策略可能具备泛化能力,适用于另一种漏洞。
作者没有提出自己的方法,主要是做实验。

