基于参数高效微调的可扩展确切机器遗忘方法
( ICLR 2025)
SISA的改进版。
没想到25年居然还有涉及的论文。
motivation
机器遗忘技术分为两大类:近似遗忘和确切遗忘。
近似遗忘无法保证完全移除该样本的影响,其对模型仍可能保留非零影响。
确切遗忘能够确保从已训练模型中彻底移除某个数据样本的影响。确切遗忘技术采用模块化系统,系统中的不同组件分别在互不重叠的数据子集上进行训练。当发生删除请求时,仅需重新训练受影响的组件即可。然而,在真实场景中,即使暂停生产系统以重新训练单个组件,也可能导致服务中断并产生巨大开销。另一种选择是绕过受影响的组件继续运行,但这可能导致性能下降,最终影响终端用户。
核心思想是在部署初始模型之前进行额外的离线训练,以降低重新训练的成本。在$S^3T$的核心中,我们采用了一种新颖的轻量级微调方法,通过依次使用不相交的数据切片训练模型各层,实现参数隔离。
方法
SISA 的一个关键缺陷在于,如果删除请求影响到所有分片的切片 1,则整个服务将无法运行,必须从头开始重新训练。另一个缺点是,每当执行删除请求时,集成中的各个模型都需要重新训练。即使仅对单个切片进行重新训练,对于大规模模型在为大量用户提供生产级服务的情况下,成本也非常高昂。一种简单的替代方案是使用最后一个可用的检查点,并定期进行重新训练。显然,随着删除请求数量的增加,整体模型的性能将逐渐下降。
$S^3T$使用LoRA来描述,但是也不仅限于LoRA。
再回顾一下LoRA,它是一种低秩更新:
$$
W=\bar W+X^TY
$$
$S^3T$的核心思想是使用不同的数据切片来训练不同的 LoRA 层。这种方法允许我们在删除某一切片的数据时,有选择性地禁用(置零)与该层相关的 LoRA 参数(X 或 Y)。
与SISA相似,它采用的也是使用不同的数据切片去训练。但是他是巧妙地将模型的不同层与不同的数据切片绑定。
它选择冻结前$i-1$层,使用$S_1+…+S_i$的数据,来训练第i层的LoRA参数。
$S^{3}T$ 的遗忘策略:
假设一个删除请求命中了 $S_3$。
- SISA 必须: 加载 $S_2$ 的检查点,用 $S_4, S_5…$ 的数据重新训练。
- $S^{3}T$ 仅需: 停用 (Deactivate)(即参数设为零)所有在训练中接触过 $S_3$ 数据的 LoRA 层。根据 $S^{3}T$ 的训练策略,第 1 层 (只用了 $S_1$) 和第 2 层 (只用了 $S_1+S_2$) 没有受到 $S_3$ 的影响。因此,系统无需任何重新训练,只需停用第 3 层、第 4 层 … 第 L 层的 LoRA 参数即可。
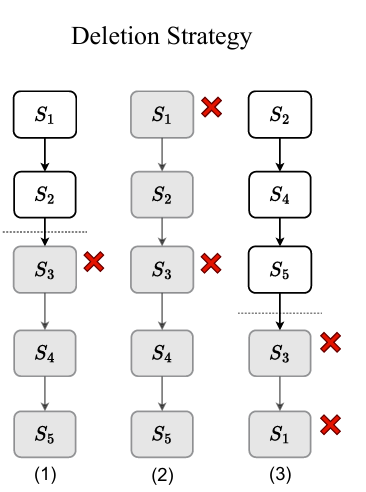
序列感知 (Sequence-Aware)
以上的过程其实有很大的缺点,比如S3有问题,则往后的S4、S5都要被删除了。
所以引入了训练预算 (Budget, B) 。它不再是为每个分片只训练一个模型,而是训练 $B$ 个模型副本,每个副本使用不同排列顺序 (Permutation) 的数据切片进行训练。
当然我们不可能训练B=L!种排列,所以我们需要序列感知。
情况 1:均匀删除先验 (Uniform Deletion Prior) (不知道哪个切片更容易被删)
使用 迭代循环轮换 (Iterative Cyclic Rotation) 。
例如 (L=3):(S1, S2, S3), (S2, S3, S1), (S3, S1, S2) 。这保证了 $S_1, S_2, S_3$ 在每个位置(第1、2、3位)都只出现一次。
情况 2:非均匀删除先验 (Non-uniform Deletion Prior) (知道某些切片(如新用户数据)更容易被删)
- 策略: 使用 基于二分图匹配的序列选择 (BMS) 。
- 这个算法的目标是,将那些最不可能被删除的切片,尽可能地排在序列的最前面(因为最前面的切片最敏感,一旦被删,整个模型报废) 。
作者也从理论证明了$S^3T$的优越性:
首先定义删除率 (Deletion Rate)为一个系统在需要从头开始重新训练之前,预期可以处理的删除请求总数。
引理 1 (Deletion Rate):
- SISA 的删除率: $\delta(SISA) \sim O(mL \log m)$。
- $S^{3}T$ 的删除率: $\delta(S^{3}T) \sim O(mL \log(m \min(B,L)))$ 。
- 结论: $S^{3}T$ 的删除率明显更高,并且随着预算 $B$ 的增加而提高(直到 $B=L$ 为止)。
引理 2 (Performance Retention):
- $S^{3}T$ 在经历 $r$ 次删除后,保持至少 $F(k)$(即 $k$ 个切片)性能的概率,显著高于 SISA。
- 结论: 增加预算 $B$ 可以有效提高系统在删除后的性能保留能力。