通过外推一个巨大且假设的语言模型的概率来解释和改进对比解码
(EMNLP 2024 Oral)
arxiv 2411.01610
对比解码相当于外推
ELM专家,ALM业余。
tokenw的logit为:
$$
L_c^{CD}(w)=L_c^{ELM}(w)-\frac{1}{T}L_c^{ALM}(w)
$$
假设ALM的温度T>1,以及logit与模型大小存在线性关系。
有一点合理性,比如模型更大,准确率可能越高,可能越自信。
$$
\begin{align}
L_c^{CD}(w)&=L_c^{ELM}(w)-\frac{1}{T}L_c^{ALM}(w)
\\&=(1-\frac{1}{T})(L_c^{ELM}(w)+\frac{1}{T}(L_c^{ELM(w)}-L_c^{ALM}(w)))
\\&=(1-\frac{1}{T})(L_c^{ELM}(w)-\frac{\frac{1}{T}}{1-\frac{1}{T}}L_c^d(w))
\end{align}
$$
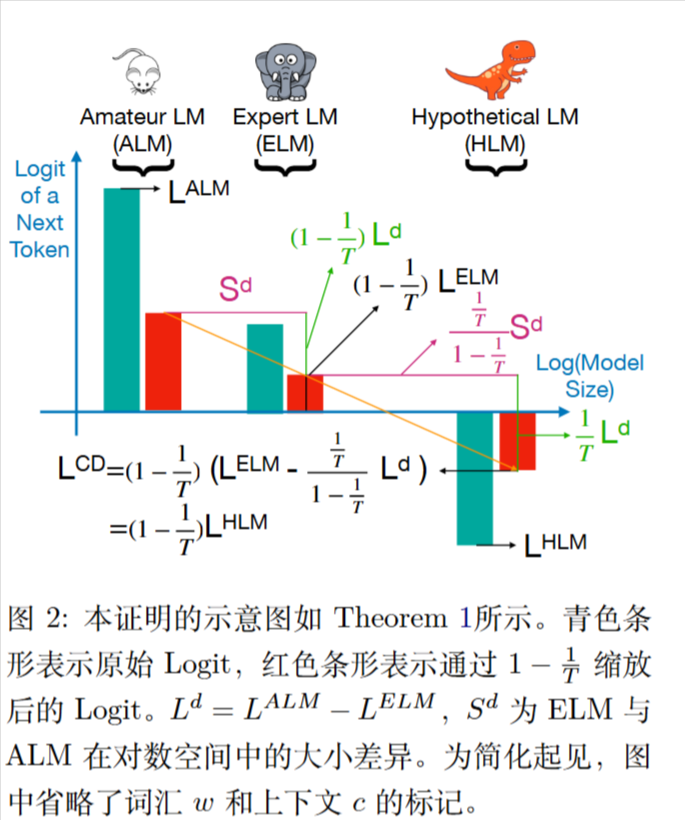
HLM和ELM的大小差异应为$\frac{\frac{1}{T}}{1-\frac{1}{T}}S^d$。
$$
\begin{align}
\log s^{HLM}
&= \log s^{ELM} + \frac{\frac{1}{T}}{1-\frac{1}{T}} S^d \\
&= \log s^{ELM} + \frac{1}{T-1}\left( \log s^{ELM} - \log s^{ALM} \right) \\
&= \frac{T}{T-1}\log s^{ELM} - \frac{1}{T-1}\log s^{ALM} \\
&= \frac{1}{T-1} \log \left( \frac{\left(s^{ELM}\right)^T}{s^{ALM}} \right)
\end{align}
$$
方法
渐进概率解码 (Asymptotic Probability Decoding, APD) ——的实现可以分为两个阶段:训练阶段和推理(测试)阶段。其核心在于通过一个创新的训练过程来微调(fine-tune)业余模型(ALM) 。
1. 训练阶段:微调业余模型(ALM)
训练阶段是整个方法最关键和最复杂的部分。它的目标不是从头训练一个新模型,而是对一个现有的、小的“业余模型”(ALM)进行微调,得到一个新版本 ALM’ 。这个新的 ALM’ 经过特殊训练,能够帮助专家模型(ELM)更好地预测出那个“无限大”的假设模型的概率。
具体实现步骤如下,整个过程在 Algorithm 1 中有总结:
第一步:数据准备和概率收集
- 选择模型家族:首先,需要一个包含多个不同尺寸模型的语言模型(LLM)家族,例如论文中使用的Pythia(包含70M, 160M, …, 6.9B等多个尺寸)。
- 收集概率:在训练语料库(例如维基百科的一个子集)上运行这个家族中的 N 个模型 。对于每一个上下文
c,记录下这些模型为下一个候选词元w输出的概率,得到一组经验概率点 $\{p(w|c, \theta _ {s_i})\} _ {i=1}^{N}$ 。 - 选择候选词元:由于词汇表太大,不可能为所有词元都建模。因此,对于每个上下文,只选择一部分候选词元
A_c,主要包括专家模型(ELM)认为最可能的Top-20个词元,以及一些随机采样的低概率词元 。
第二步:概率曲线参数化
为了能够对外推进行建模,APD需要拟合一条穿过上述经验概率点的曲线。
- 统一曲线方向:因为概率曲线可能随模型增大而上升或下降,为了简化建模,论文首先使用一个预处理步骤
R(·),将所有上升的概率曲线“翻转”(通过1-p的方式)为下降曲线。 - 选择曲线函数:使用一个简单的指数衰减函数来参数化这条(翻转后的)下降曲线 。这个函数的形式如下(见公式(7)) :
$$
\hat{p} _ {w,c}(s) = \hat{P’} _ {c}^{AP}(w) + a _ {w,c}e^{-max(0, b _ {w,c}(s-d _ {w,c}))}
$$s是模型大小的对数。- $\hat{P’} _ {c}^{AP}(w)$ 是模型尺寸趋于无穷大时的渐进概率,这也是我们最终想要预测的目标。
a, b, d是控制曲线形状的三个正参数。
第三步:使用MLP作为能量网络进行拟合
- MLP的角色:论文使用一个4层的多层感知机(MLP)来确定上述曲线的参数
a, b, d。这个MLP不直接预测概率,而是扮演一个“能量网络”或“评估器”的角色 。 - MLP的输入和输出:
- 输入:MLP接收两组数据:(1) 从不同大小模型收集到的经验概率点 $\{p’(w|c, \theta _ {s_i})\} _ {i=1}^{N}$ ;(2) 由当前微调中的 ALM’ 和 ELM 计算出的预测渐进概率 $\hat{P’} _ {c}^{AP}(w)$。
- 输出:MLP输出曲线参数
a, b, d。
- 核心机制:如果 ALM’ 预测出的渐进概率是“好的”,那么MLP就能很容易地找到一组
a, b, d参数,使得生成的曲线能够很好地拟合所有经验概率点 。反之,如果预测的渐进概率“不好”,MLP将无法生成一条能同时穿过所有已知点的平滑曲线,从而导致很高的损失 。
第四步:定义损失函数并进行反向传播
为了训练 ALM’ 和 MLP,论文设计了一个包含三个部分的组合损失函数:
- 损失1 ($L_1$):拟合损失。计算MLP生成的曲线与真实经验概率点之间的均方根误差(RMSE),确保曲线能很好地拟合已知数据。
$$
L _ {1} =
\sqrt{
\frac{1}{Z \cdot (N-1)}
\sum _ {c \in B}
\sum _ {w \in A _ {c}}
\sum _ {i=1}^{N-1}
\left(
p’(w \mid c, \theta _ {s _ {i}}) - \hat{p} _ {w,c}(s _ {i})
\right)^{2}
}
$$
其中$A_c$为ELM的top token候选,归一化项$Z=|B||A_c|$。
- 损失2 ($L_2$):过高惩罚损失。为了防止模型对下降曲线的渐进概率预测过高,这个损失项专门惩罚那些在ELM尺寸上预测概率超过真实观测概率的情况。
$$
L_2 = \sqrt{\frac{1}{Z} \sum _ {c \in B} \sum _ {w \in A_c} \max(0, \hat{p} _ {w,c}(s_N) - p’(w|c, \theta _ {s_N}))}
$$
- 损失3 ($L_3$):正则化损失。为了防止微调后的 ALM’ 与原始的 ALM 偏离太远,这个损失项计算它们输出对数(logit)之间的差异,起到了稳定训练的作用。
$$
L_3 = \sqrt{\frac{1}{Z} \sum _ {c \in B} \sum _ {w \in A_c} (L_c^{ALM’}(w) - L_c^{ALM}(w))^2}
$$
将这三个损失加权求和 Loss = L_1 + \lambda_2 L_2 + \lambda_3 L_3 ,然后通过反向传播,梯度会从损失函数流经MLP,再流回到 ALM’。这样,ALM’ 的参数就会被更新,使其能够生成一个更好的渐进概率预测,从而让MLP更容易拟合曲线,最终使总损失降低。
2. 推理(测试)阶段:高效生成文本
一旦训练完成,我们就得到了一个优化后的业余模型 ALM’ 。推理阶段就变得非常简单和高效了:
- 抛弃复杂组件:在推理时,不再需要MLP和那些用于训练的中间尺寸模型。
- 使用新公式:直接使用微调好的 ALM’ 替换掉原始CD公式中的 ALM。最终的概率计算公式(见公式(5))如下:
$$
\hat{P} _ {c}^{AP}(w) = \text{Softmax}(L _ {c}^{ELM}(w) - \frac{1}{T}L _ {c}^{ALM’}(w))
$$ - 效率:这个计算过程和原始的对比解码(CD)完全一样,都只需要一次专家模型(ELM)和一次业余模型(ALM’)的前向传播。因此,APD在实现更复杂的外推的同时,没有增加任何额外的推理成本 。