MokA:Multimodal Low-Rank Adaptation for MLLMs
(NIPS 2025)
motivation
现在的多模态大模型的微调直接接借用大型语言模型(LLM)的微调技术,往往忽略了多模态场景的内在差异,导致非文本模态的信息未能被充分利用。该论文的核心观点是,有效的MLLM微调应同时包含**单模态自适应(unimodal adaptation)和跨模态自适应(cross-modal adaptation)**两个关键部分 。
文本 token 推理能够达到与常规全模态情景相当的性能。然而,非文本 token(如音频或视觉)推理则导致性能显著下降。
MokA 保留了广泛采用的低秩分解矩阵,但重新定义了矩阵 A 和B 的角色,以更好地适应多模态特性。具体而言,矩阵 A 被设计为模态特定的,允许每个模态独立压缩信息,从而避免其他模态的干扰。随后,引入交叉注意力机制以加强文本 token与非文本 token 之间的交互,突出任务相关特征。最后,一个共享的多模态矩阵 B 将单模态低秩表示投影到一个统一的空间中,促进跨模态的有效对齐。
算法
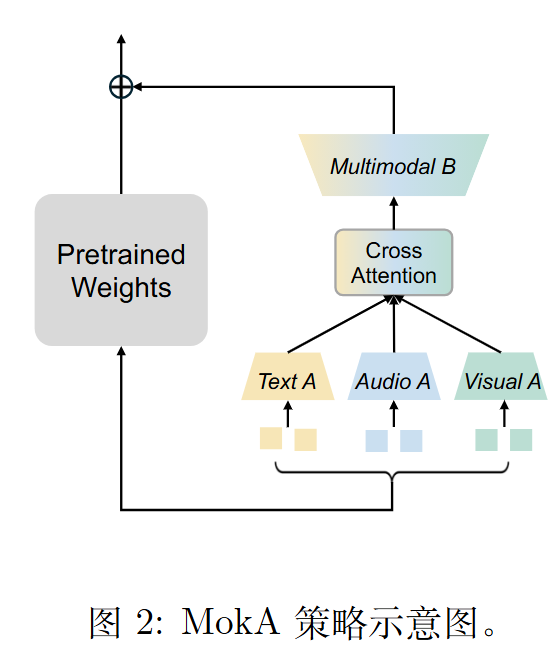
我们针对音频 (audio, a)、视觉 (visual, v) 和 文本 (text, t) 三种模态的场景。
单模态矩阵
对于 MLLM 中的任意一个预训练权重矩阵 $W_0 \in \mathbb{R}^{d \times k}$,MokA 的目标是学习一个低秩更新 $\Delta W$,使得最终的权重为 $W_0 + \Delta W$。其前向传播的计算流程如下:
输入序列 $x$ 是由不同模态的词元(tokens)拼接而成:
$$x = [x^a; x^v; x^t]$$
其中,$x^a, x^v, x^t$ 分别代表音频、视觉和文本模态的词元序列。
为了独立地捕捉每个模态的特有信息,避免模态间的相互干扰,MokA 为每种模态都使用一个独立的、不共享的低秩矩阵 $A^i$。其中 $i \in {a, v, t}$。
每个模态的词元序列 $x^i$ 会被其对应的矩阵 $A^i \in \mathbb{R}^{r \times k}$ (其中 $r \ll \min(d, k)$ 是低秩维度) 独立地映射到一个低秩空间中。
该步骤的输出为:
$$Ax = [A^a x^a; A^v x^v; A^t x^t]$$
任务为中心的跨注意力机制 (Task-centric Cross-Attention)
在指令微调场景下,文本词元通常描述任务,而非文本词元提供上下文信息。为了有效捕捉任务描述与上下文之间的语义关联,MokA 在低秩空间中引入了跨注意力机制,以显式地增强跨模态交互。
该机制的设计是:使用非文本模态 (音频、视觉) 的表征作为查询 (Query),并使用文本模态的表征作为键 (Key) 和值 (Value)。这样做可以在不改变文本原有表征的前提下,将与任务相关的文本信息融入到非文本模态中。
计算音频模态的注意力增强:
$$Att _ {a,t,t} = \text{softmax}\left(\frac{(A^a x^a)(A^t x^t)^T}{\sqrt{N_t}}\right) A^t x^t$$
其中 $N_t$ 是文本词元的数量。计算视觉模态的注意力增强:
$$Att _ {v,t,t} = \text{softmax}\left(\frac{(A^v x^v)(A^t x^t)^T}{\sqrt{N_t}}\right) A^t x^t$$通过残差连接更新非文本表征:
- 增强后的音频表征: $A^a x^a + Att _ {a,t,t}$
- 增强后的视觉表征: $A^v x^v + Att _ {v,t,t}$
经过此步骤,整合了跨模态信息的序列变为:
$$Ax _ {enhanced} = [A^a x^a + Att _ {a,t,t}; A^v x^v + Att _ {v,t,t}; A^t x^t]$$
线性的投影(Wq 、Wk 和 Wv )并未包含在交叉注意力模块中,因为在这种情况下,每个模态的低秩矩阵 A 实际上可以被视为注意力中的线性投影。
共享多模态矩阵B
在增强了跨模态交互之后,需要将所有模态的低秩表征投影回原始的高维空间,以实现最终的跨模态对齐。MokA 使用一个所有模态共享的矩阵 $B \in \mathbb{R}^{d \times r}$ 来完成这个任务。
MokA 旁路计算的最终输出为:
$$BAx = [B(A^a x^a + Att _ {a,t,t}); B(A^v x^v + Att _ {v,t,t}); BA^t x^t]$$
最终输出
一个应用了 MokA 的层的最终输出 $h$ 是原始预训练权重 $W_0$ 的输出与 MokA 旁路输出的总和:
$$h = W_0 x + \Delta W x$$将 $\Delta W x$ 的计算展开,可以清晰地看到单模态和跨模态自适应两个部分:$$h = W_0 x + \underbrace{[BA^a x^a; BA^v x^v; BA^t x^t]} _ {\text{unimodal adaptation}} + \underbrace{[BAtt _ {a,t,t}; BAtt _ {v,t,t}; 0 _ {N_t}]} _ {\text{cross-modal adaptation}}$$
其中 $0 _ {N_t}$ 表示一个零向量,因为文本词元在跨注意力步骤中未被改变。
这个公式清晰地展示了 MokA 如何通过其结构设计,在一次前向传播中同时实现了对各个模态的独立调整以及模态间的显式交互。
为了保证训练开始时的稳定性,初始化策略与 LoRA 类似:
- 所有单模态矩阵 $A^i$ 使用 Kaiming 均匀分布进行初始化。
- 共享的投影矩阵 $B$ 初始化为全零。
这确保了在训练开始时,整个更新量 $\Delta W = 0$,模型从其原始预训练状态平稳启动。
实验
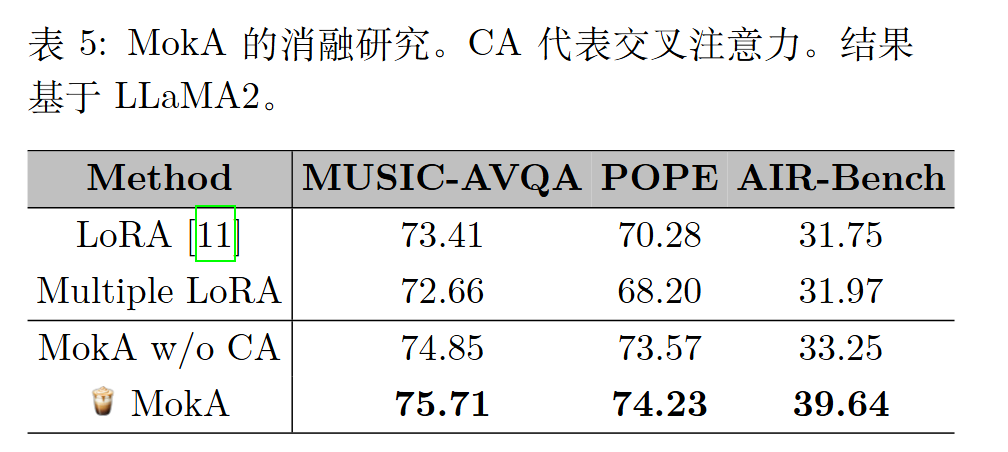
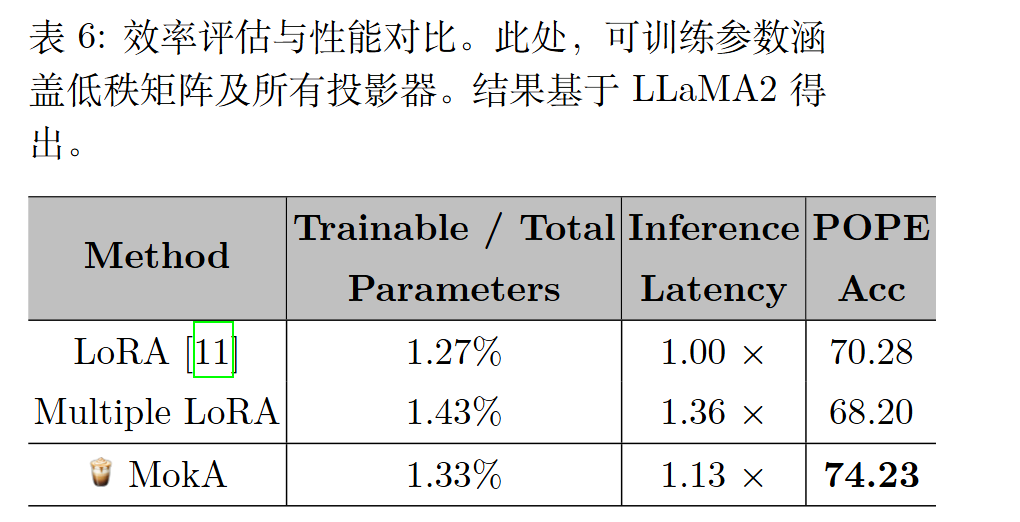
在显式跨模态整合(如交叉注意力)过程中,与给定模态更相关的文本 token 可以获得更高的注意力权重。例如,token“sound”在与音频模态的关系中获得了更大的注意力。这种跨模态整合可以更好地促进文本 token 与非文本token 之间的对齐和交互。
