Nullu:通过 HalluSpace 投影减轻大型视觉-语言模型中的对象幻觉
(CVPR 2025)
在视觉语言模型中,物体幻觉(Object Hallucinations,OH)指的是模型在生成图像描述时,错误地提到了图像中并不存在的物体。
方法
构建成对视觉-语言输入数据集。这两个输入具有相同的图像但不同的文本提示,其中一个是包含真实值$x ^ {−}_i$的正确描述,该描述准确描述了图像中的物体,另一个是包含幻觉描述$x^+_i$的文本。
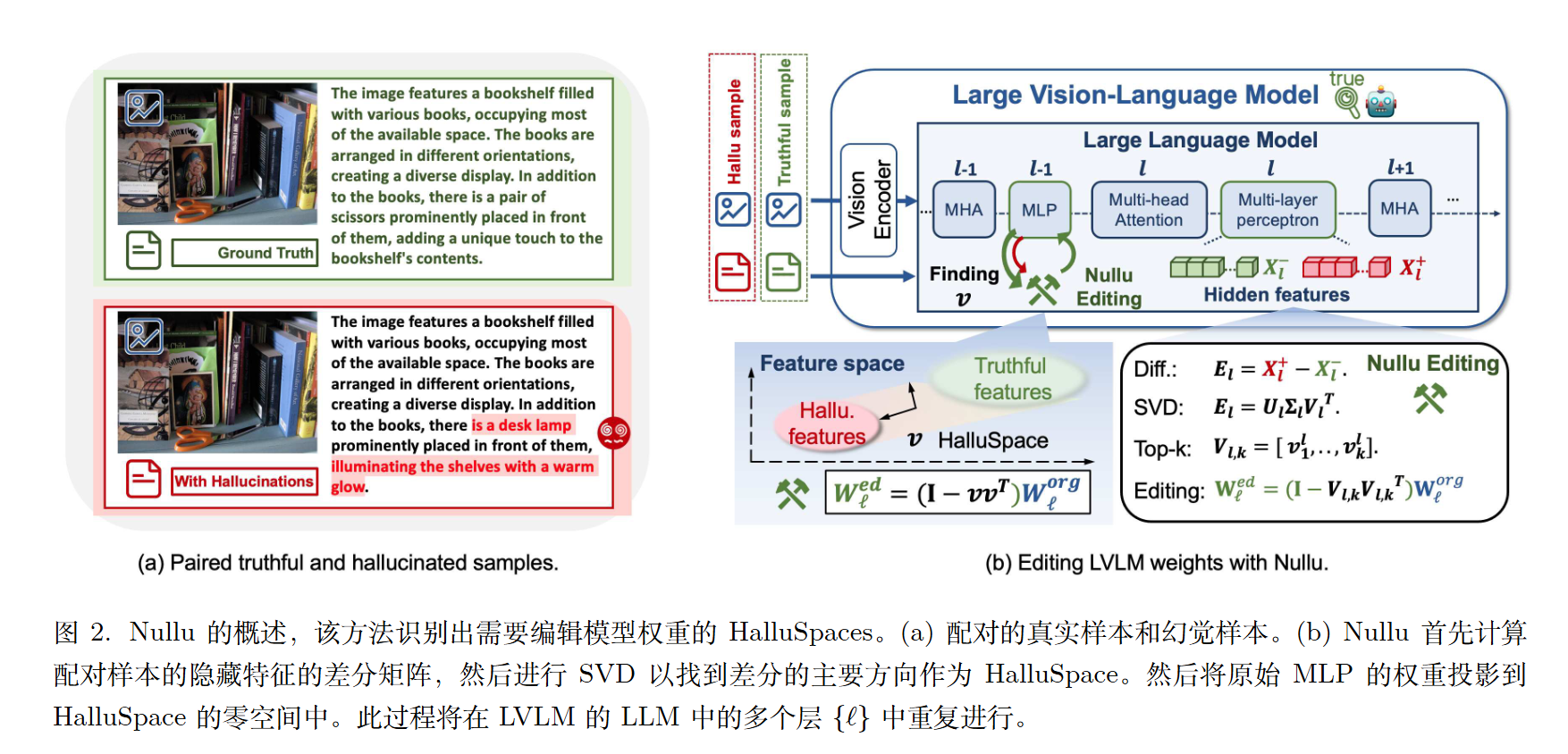
第$\ell$层的差分矩阵$E_\ell$为$E_\ell=X^+ _ \ell-X^- _ \ell$.
然后我们可以对$E_\ell$进行SVD分解。
然后选取top k 奇异值的右奇异向量。(左代表样本维度,右代表特征维度。)
而$V _ {\ell,k}$的零空间是$(I-V _ {\ell,k}V _ {\ell,k}^T)$。

故我们将MLP的权重投影到零空间上,即$W_\ell ^ {ed}=(I-V _ {\ell,k}V _ {\ell,k}^T)W _ {\ell} ^ {org}$。
和DPO的联系
$\mathcal{L} _ {DPO} = -\mathbb{E} _ {(x,y ^ {+},y ^ {-})\sim\mathcal{D}}[\log \sigma(\beta \log\frac{\pi _ {\theta}(y ^ {+}|x)}{\pi _ {ref}(y ^ {+}|x)} - \beta \log\frac{\pi _ {\theta}(y ^ {-}|x)}{\pi _ {ref}(y ^ {-}|x)})]$
为了简化,我们定义 $\hat{r} _ {\theta}(x, y) = \beta \log\frac{\pi _ {\theta}(y|x)}{\pi _ {ref}(y|x)}$。
那么损失函数可以写成:
$\mathcal{L} _ {DPO} = -\mathbb{E}[\log \sigma(\hat{r} _ {\theta}(x, y^+) - \hat{r} _ {\theta}(x, y^-))]$
令 $z = \hat{r} _ {\theta}(x, y^+) - \hat{r} _ {\theta}(x, y^-)$,那么 $\mathcal{L} _ {DPO} = -\log \sigma(z)$ (暂时忽略期望 $\mathbb{E}$)。
梯度可以分解为:
$\nabla_W \mathcal{L} _ {DPO} = \frac{\partial \mathcal{L} _ {DPO}}{\partial z} \cdot \nabla_W z$
首先计算第一部分 $\frac{\partial \mathcal{L} _ {DPO}}{\partial z}$:
- $\frac{d}{dz} \sigma(z) = \sigma(z)(1-\sigma(z))$
- $\frac{d}{dz} \log(u) = \frac{1}{u}$
- 因此,$\frac{d}{dz} \log(\sigma(z)) = \frac{1}{\sigma(z)} \cdot \sigma(z)(1-\sigma(z)) = 1 - \sigma(z)$
- 所以,$\frac{\partial \mathcal{L} _ {DPO}}{\partial z} = -\frac{\partial}{\partial z} \log \sigma(z) = -(1 - \sigma(z)) = \sigma(z) - 1$
论文中假定,梯度是在初始化状态下计算的,即策略模型与参考模型相等($\pi_\theta = \pi _ {ref}$)。
在这种情况下:
- $\log\frac{\pi _ {\theta}(y|x)}{\pi _ {ref}(y|x)} = \log(1) = 0$
- 所以 $z = \hat{r} _ {\theta}(x, y^+) - \hat{r} _ {\theta}(x, y^-) = 0 - 0 = 0$
- 当 $z=0$ 时,sigmoid函数 $\sigma(0) = \frac{1}{1+e^0} = \frac{1}{2}$
- 代入第二步的结果,我们得到 $\frac{\partial \mathcal{L} _ {DPO}}{\partial z} | _ {\pi_\theta = \pi _ {ref}} = \sigma(0) - 1 = \frac{1}{2} - 1 = -\frac{1}{2}$
接着我们计算梯度的第二部分 $\nabla_W z$:
$\nabla_W z = \nabla_W (\hat{r} _ {\theta}(x, y^+) - \hat{r} _ {\theta}(x, y^-))$
$= \nabla_W (\beta \log\frac{\pi _ {\theta}(y ^ {+}|x)}{\pi _ {ref}(y ^ {+}|x)}) - \nabla_W (\beta \log\frac{\pi _ {\theta}(y ^ {-}|x)}{\pi _ {ref}(y ^ {-}|x)})$
由于 $\pi _ {ref}$ 不依赖于我们要优化的权重 $W$,它的梯度为零。
$= \beta (\nabla_W \log \pi _ {\theta}(y ^ {+}|x) - \nabla_W \log \pi _ {\theta}(y ^ {-}|x))$
进一步的,论文使用了一个简化的逻辑回归模型来表示概率:
$\pi_W(y|x) = Z_W ^ {-1} \exp(\sum _ {m=1} ^ {M} o _ {y_m} ^ {\top} W x_m)$
取对数后得到:
$\log \pi_W(y|x) = \sum _ {m=1} ^ {M} o _ {y_m} ^ {\top} W x_m - \log Z_W$
现在对它求关于 $W$ 的梯度。
- $\nabla_W (\sum o _ {y_m} ^ {\top} W x_m) = \sum \nabla_W (\text{Tr}(o _ {y_m} ^ {\top} W x_m)) = \sum o _ {y_m} x_m ^ {\top}$ (这是矩阵微积分的标准结论)
- $\nabla_W (\log Z_W)$ 这一项是存在的,但论文指出,当我们计算 $y^+$ 和 $y^-$ 之间的差值时,这个归一化项的梯度会相互抵消掉。
因此,我们只关注 logits 部分的梯度。为了简化(如论文中只考虑M=1的情况):
$\nabla_W \log \pi_W(y|x) = o_y x ^ {\top}$
代入第四步的结果:
$\nabla_W z = \beta (o _ {y^+}(x^+) ^ {\top} - o _ {y^-}(x^-) ^ {\top})$
现在,我们将前面的结果组合起来:
$\nabla_W \mathcal{L} _ {DPO} | _ {\pi_\theta = \pi _ {ref}} = \frac{\partial \mathcal{L} _ {DPO}}{\partial z} \cdot \nabla_W z$
$= (-\frac{1}{2}) \cdot \beta (o _ {y^+}(x^+) ^ {\top} - o _ {y^-}(x^-) ^ {\top})$
考虑到损失函数是所有样本的期望(平均值),我们引入求和与系数 $-\frac{1}{N}$。常数 $1/2$ 可以合并到超参数 $\beta$ 中。这样,我们就得到了以下形式:
$\nabla_W \mathcal{L} _ {DPO} = -\frac{\beta}{N}\sum _ {i=1} ^ {N}(o _ {y _ {i}} ^ {+}(x _ {i} ^ {+}) ^ {\top}-o _ {y _ {i}} ^ {-}(x _ {i} ^ {-}) ^ {\top})$
最后,为了展示“特征差异”和“输出差异”,论文对这个结果做了一个简单的代数变换。通过加上和减去同一个项 $o _ {y_i^+}(x_i^-)^\top$:
$\nabla_W \mathcal{L} _ {DPO} \propto -(o _ {y^+}(x^+)^\top - o _ {y^-}(x^-)^\top)$
$= -(o _ {y^+}(x^+)^\top \color{blue}{- o _ {y^+}(x^-)^\top + o _ {y^+}(x^-)^\top} \color{black}{- o _ {y^-}(x^-)^\top})$
$= -( [o _ {y^+}(x^+)^\top - o _ {y^+}(x^-)^\top] + [o _ {y^+}(x^-)^\top - o _ {y^-}(x^-)^\top] )$
$= -( o _ {y^+} (x^+ - x^-)^\top + (o _ {y^+} - o _ {y^-}) (x^-)^\top )$
实验
理想情况下,如果HalluSpace有效代表了这些偏差,那么将测试样本映射到 HalluSpace 时,差异向量应该具有较大的投影分量。
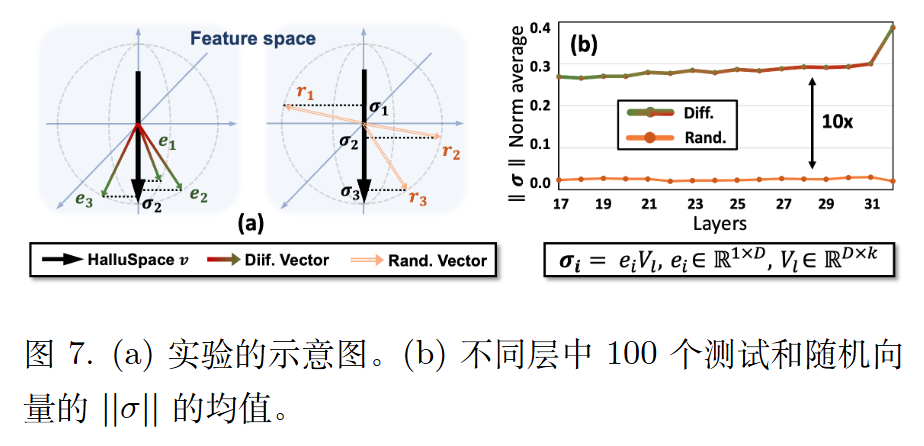
另外的一些实验结果:
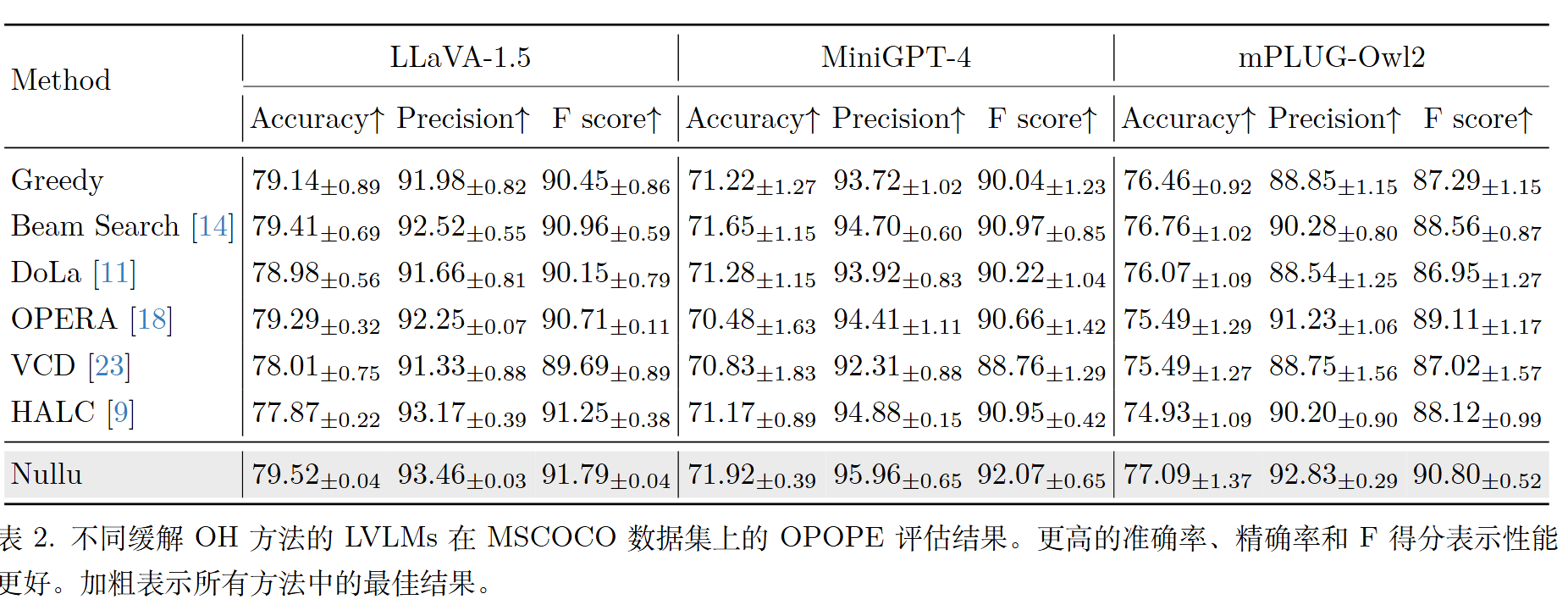
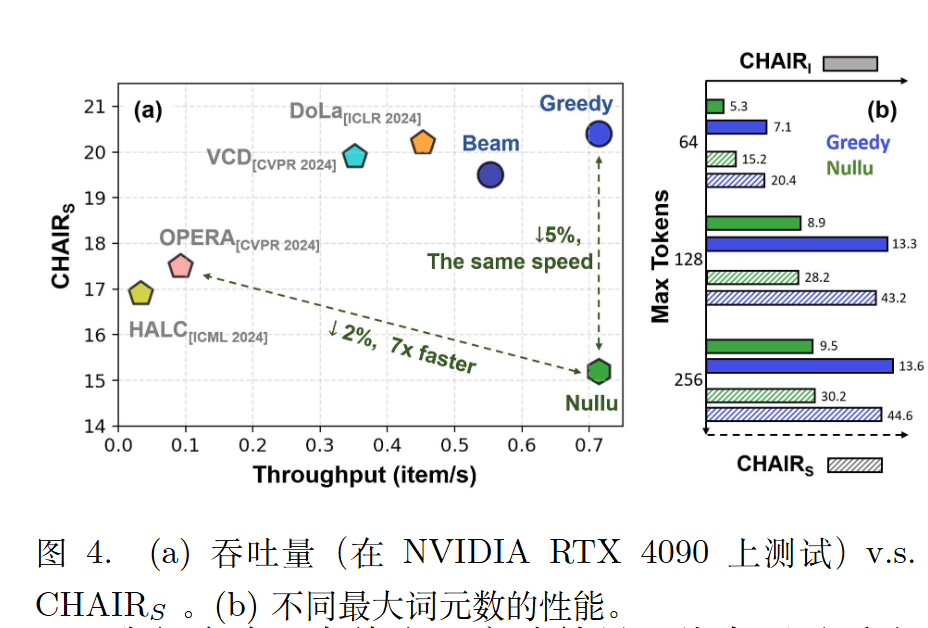
后续
Chao Shen后续也做了一些相关的工作。2505.17812
但很像2410.15778的《Reducing Hallucinations in Vision-Language Models via Latent Space Steering》,同样都是使用$h=h+\alpha v^T$的形式。