SINDER:Repairing the Singular Defects of DINOv2
(ECCV 2024 Oral)
动机
不同图像中的缺陷 patch token 几乎相同。
为了验证这一点,作者计算了每张图像的平均缺陷 token,然后计算它们之间的平均成对角度,结果为 5.5 度。这证实了最后一层中的缺陷方向本质上与输入图像无关。这一观察结果与前人中的观点不同,前人声称高范数token 包含图像级别的全局信息。(有点类似attention sinks)
奇异缺陷方向的定义完全源自预训练网络的权重;在推理过程中,它并不依赖于输入图像。
根据作者的统计量,这些高范数 token 主要不包含任何输入信息,无论是局部的还是全局的。
作者从power iteration中受到启发,这是一种求主特征向量的方法,迭代过程为$b_{k+1}=\frac{Ab_k}{||Ab_k||}$。
促使作者从奇异值分解的角度来探讨缺陷问题。
注意作者不区分奇异的缺陷方向与其相反方向。
算法
Singular Defect Repairing(SIN-DER)
SINDER 旨在通过修改少量参数,使用平滑的正则化来修复前向传播中遇到的第一个缺陷层。
首先定义logit$l_t$为规范化patch token与$v_i$之间内积的绝对值。
$$
l_t=\left| \frac{x_t}{||x_t||}\cdot v_i\right| \tag{5}
$$
然后将缺陷 Token 集合 D 定义为那些偏离平均 Logit 超过 掩码阈值μ = 4 倍标准差的 Token。
对于一个有缺陷的token,使用其3x3空间邻近tokens的加权平均来定义其学习目标,另$x_{t1}$为$x_t$的邻近token。
计算系数:
$$
c_{tt_1}=\frac{exp(-l_{t1}/\tau)}{\sum_{s\in N_t}exp(-l_s/\tau)}
$$
然后将该系数与3x3的高斯核相乘并归一化。
并线性组合为token$x_t$的学习目标:
$$
\tilde x_t=\sum_{t1\in N_t} \tilde c_{tt1}x_{t1}
$$
损失函数:
$$
L=\frac{1}{|D|}\sum_{t\in D}||x-\tilde x_t|| \tag{8}
$$
进一步限制学习参数数量:
考虑到使用比原始训练集少得多的图像对模型进行微调,控制可训练参数的数量以避免损害模型在下游任务中的泛化能力变得至关重要。
具体而言,作者在微调过程中使用SVD,并冻结参数U和V。

实验
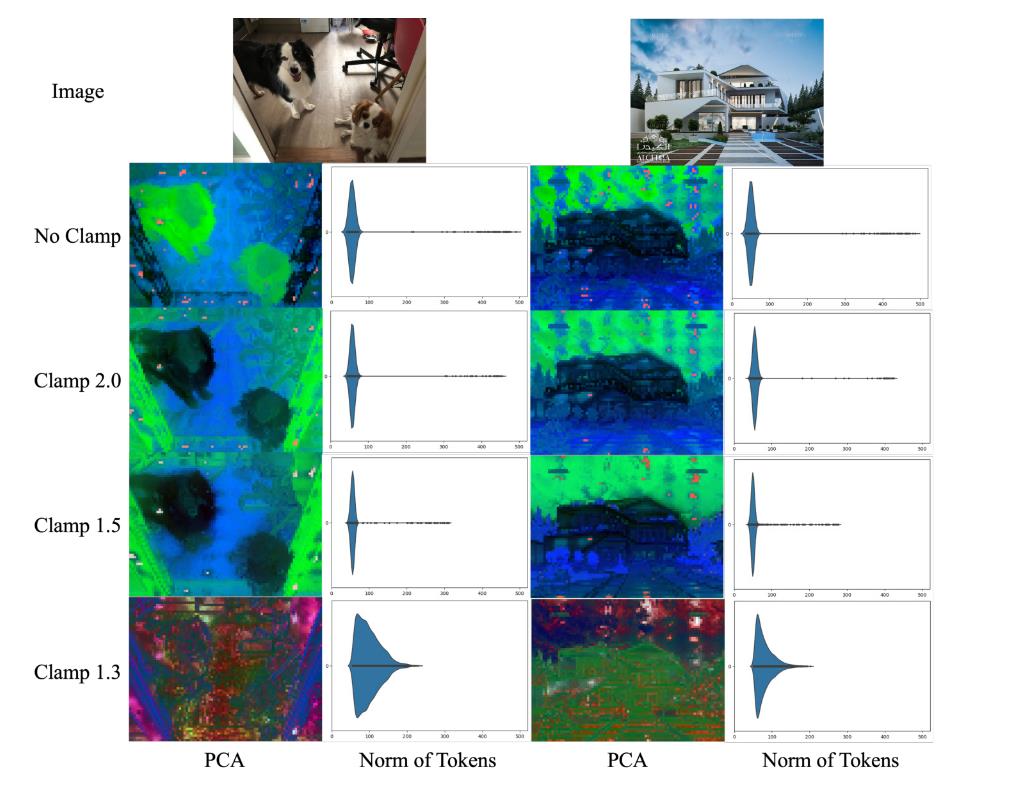
如果我们只是简单的对奇异值clip,则结果如下。随着 γ 的减小,缺陷补丁的范数也随之减小,缺陷token 的数量也减少。然而,当 gamma 过小时,特征图的语义似乎被破坏。
所以使用学成的最优奇异值更好,而不是根据某些手动设计的阈值进行裁剪。
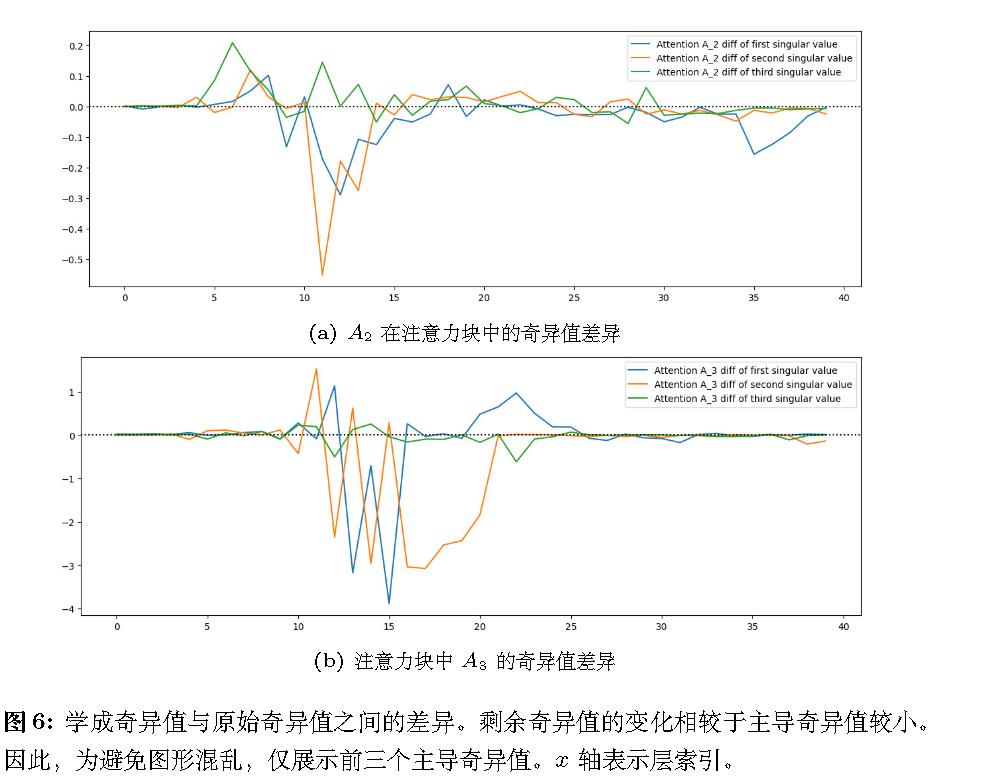
学成奇异值与原始奇异值之间的差异:
线基本都在下面。
后续
作者后续又用左奇异向量预测“爆炸”后的方向;用右奇异向量解释“触发”条件(爆炸子空间);用特征值分解解释“衰减”层的行为。2502.07004