线性注意力速览
自注意力机制是Transformer模型的重要部分,但是自注意力的计算和内存的复杂度都与序列长度的二次方成正比,这带来了巨大的计算和内存瓶颈。于是乎,就有了线性注意力的提出。
最简单的形式
我们知道标准的attention可以写成:(忽略缩放因子)
$$
O=softmax(QK^T)V
$$
现在的计算顺序是$(QK^T)V$,如果我们能把计算顺序改为$Q(K^TV)$,那么计算复杂度将从$O(N^2d)$到$O(Nd^2)$。
那我们该如何把softmax化掉呢?
我们可以联想到SVM等中所用到的核函数:K( x, x′) =φ( x) ⋅φ( x′)。
于是我们也可以寻求$exp(q,k)\approx\phi(q)^T\psi(k)$。
而《Efficient Attention: Attention with Linear Complexities》给出的选择是,对Q和K的不同维度进行归一化:$P=softmax_d(Q)softmax_N(K)^TV$。
更多的其他方法还有Random Feature Attention、Performer等。
进一步的我们可以省略为$O=Q(K^TV)$。
我们可以写成$o_t=(\sum_{j=1}^t v_jk_j^T)q_t$。
我们把$q_t$分开,也就是$o_t=S_tq_t$,$S_t=S_{t-1}+v_tk_t^T$
统一形式
我们得到了上面的式子,可以看成attention可以写成以$S_t$为state的线性RNN的形式。
进一步的我们可以假定统一形式为:
$$
S_t=A_tS_{t-1}+B_t
$$
当然我们也不是胡乱设置A和B的,这条式子类似梯度下降的迭代,故我们也可以参考梯度下降。这正是《Learning to (Learn at Test Time): RNNs with Expressive Hidden States》的做法:
我们希望学习一个函数$M:key\to value$,并定义一个距离度量$loss_M(key,value)=dis(M(key),value)$,梯度下降为$M_{next}=M-\beta\nabla loss_M(k,v)$。
对于距离我们可以采取负点积或(平方)欧几里得距离,也就引出了以下的线性注意力:
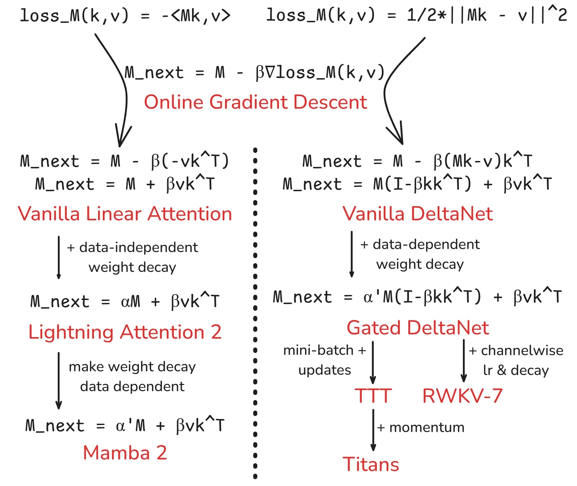
而(平方)欧几里得距离的梯度下降实际上可以与机器学习中的Delta rule联系起来,这也就是DeltaNet名字的由来。
虽然$B_t$大多为$v_tk_t^T$的倍数,但也有不符合这一形式的。这也是为什么我们这里采用$S_t=A_tS_{t-1}+B_t$而不是$S_t=A_tS_{t-1}+B_tv_tk_t^T$。
| 线性注意力 | $A_t$ | $B_t$ |
|---|---|---|
| Vanilla Linear Attention | I | $v_tk_t^T$ |
| RetNet(2023.07) | $\gamma$ | $v_tk_t^T$ |
| Mamba 2(2024.05) | $diag(\alpha_tI)$ | $v_tk_t^T$ |
| DeltaNet(2024.06) | $\alpha_i(I-\beta_tk_tk_t^T)$ | $\beta_tv_tk_t^T$ |
| Gated DeltaNet(2024.12) | $I-\beta_tk_tk_t^T$ | $\beta_tv_tk_t^T$ |
| RWKV-5(2023.11)/RWKV-6(2024.05) | $diag(w_t)$ | $v_tk_t^T$ |
| HGRN-2(2024.07) | $diag(w_t)$ | $v_t(1-w_t)^T$ |
| RWKV-7(2025.03) | $diag(w_t)-\kappa_i(a_i\odot \kappa_i^T)$ | $v_tk_t^T$ |
RKKV-7较复杂,$\kappa$代表对键进行部分移除,还会进行归一化,w代表衰减率。(且RWKV并不是$o_t=S_qo_t$的形式,像RWKV6则是$o_t=(S_{t-1}+(d\odot v_t)k_t^T)q_t$,似乎在论文中并未找到如何设计的缘由,可能更多是Bo Peng的灵感一现)