传统kmeans并不是（局部）最优

(ICML 2025) 《Modified K-means Algorithm with Local Optimality Guarantees》

K-means是广泛使用的聚类算法，尽管它不一定能保证全局最优，但大家都约定速成地认为K-means会收敛到局部最优解。

但其实不然。

定义问题

在提出反例之前我们先提出一些定义。

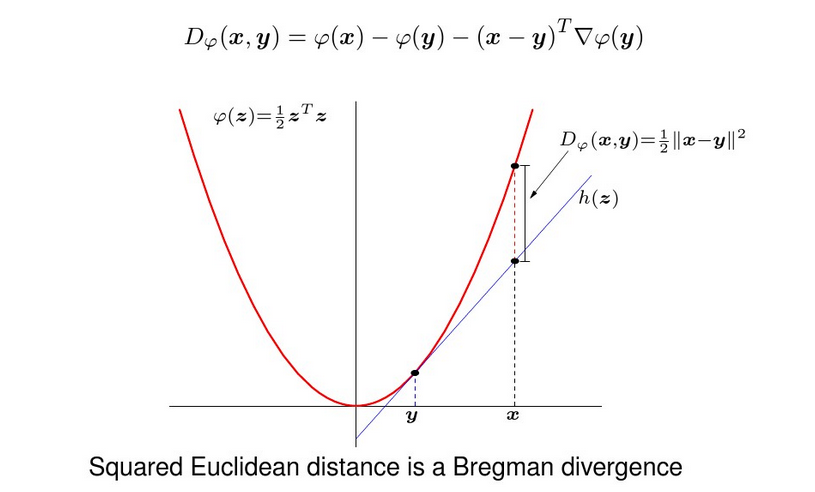
我们将广泛使用的欧式距离拓展到Bregman 散度。
$$
D_\phi(x,y)=\phi(x)-\phi(y)-<x-y,\nabla\phi(y)>
$$
Bregman散度是借用一个严格凸函数φ（·），该散度即为φ（x）和h（x）的差，其中h（x）为φ（y）在x处的线性近似。

更多的：

两种局部最优的定义：

D-local: Discrete locally optimal solution

即若把某个数据点移动到任意簇后，损失都会升高。

C-local: Continuous locally optimal solution

即在某个数据点的附近一个领域内，无论怎么移动，损失都会升高。

可以看出D-local更强。

反例

点的数量为 N = 5，簇的数量为K = 2，相似度度量为 $D(x, y) =||x-y||^2_2$，给定的数据集和初始中心如下：

x1 = −4, x2 = −2, x3 = 0, x4 = 1.5, x5 = 2.5,
c1 = x3 = 0, c2 = x5 = 2.5
$$
p^\ast=\begin{bmatrix}
1,1,1,0,0\\0,0,0,1,1
\end{bmatrix},c_1^\ast=-2,c_2^\ast=2
$$
但是他并不满足C-local或D-local。

改进

为了满足C-local，我们找数据点 n 满足至少两个或以上的簇中心在可允许误差范围内同样近。修改它的簇为另外的簇。

为了满足D-local，我们检查所有的数据点，遍历移动到其他簇是否损失会降低。