流模型与流匹配

流模型与流匹配介绍。

归一化流（Normalizing Flow）

先导

我们首先会定义了一个分布 $p _ {z}(z)$,有时也称为基础分布，以及一个由深度神经网络给出的非线性函数 $x=f(z,w)$，该函数将潜在空间（latent space）转换为数据空间。

$p _ {z}(z)$ 会尽可能简单,例如高斯分布，以便从这种模型中进行采样。

为了衡量分布的相似度，$g^\ast =argmax\sum logP(x)\approx argmin (KL(P _ {data}||P_G))$，我们需要计算此模型的似然函数,我们需要数据空间分布，这取决于神经网络的逆函数。

我们将其写为 $z=g(x,w)$，它满足 $z=g(f(z,w),w)$。即对于w的每个值,函数 $f(z,w)$ 和 $g(x,w)$ 是可逆的。

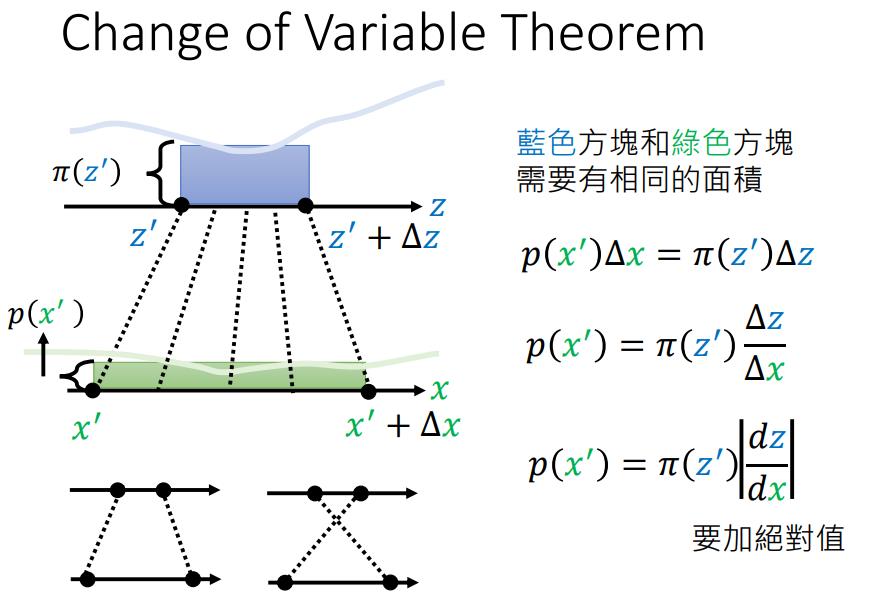
然后我们可以使用变量变换公式（change of variable theorem）来计算数据密度:

$$
p _ {x}(x|w)=p _ {z}(g(x,w))|det J(x)|
$$

其中 $J(x)$ 是雅可比矩阵，$J _ {ij}(x)=\frac{\partial g _ {i}(x,w)}{\partial x _ {j}}$ 。

然而，要求可逆映射的一个后果是，隐式空间的维度必须与数据空间的维度相同，这可能导致高维数据(如图像，动辄就是几百乘几百的维度)的大型模型的复杂性增加。比如计算 $D\times D$ 矩阵的行列式的成本是 $\mathcal{O}(D^{3})$。

所以，我们希望对模型施加一些进一步的限制,以便更有效地计算雅可比矩阵行列式。

如果我们考虑一个独立数据点训练集 $\mathcal{D}={x _ {1},…,x _ {N}}$，则：

$$
\begin{align}
ln~p(\mathcal{D}|w)&=\sum _ {n=1}^{N}ln~p _ {x}(x _ {n}|w)
\\
&=\sum _ {n=1}^{N}{ln~p _ {z}(g(x _ {n},w))+ln|det~J(x _ {n})|}
\end{align}
$$

并且我们的目标是通过似然函数来训练神经网络。为了能够模拟各种分布,我们希望转换函数 $x=f(z,w)$ 具有高度的灵活性,因此我们使用深度 神经网络架构。如果我们使网络中的每一层都是可逆的,那么我们可以确保整个函数是可逆的。为了看到这一点,考虑三个连续的变换,每个变换对应网络的一层,形式如下:

$$
x=f^{A}(f^{B}(f^{C}(z)))
$$

那么逆函数由下式给出：

$$
z=g^{C}(g^{B}(g^{A}(x)))
$$

对于雅克比矩阵也可以使用链式法则化为各个层的乘积。

这种建模分布的方法称为归一化流（Normalizing Flow）。流，是因为通过一系列映射转换概率分布的过程与流体的流动有些类似。归一化，是因为逆映射的效果是将复杂的数据分布转换为归一化形式,通常是高斯或正态分布。

耦合流（Coupling Flows）

我们的目标是为单个可逆函数层,以便我们可以将许多层组合在一起来定义一个高度灵活的可逆函数类。

首先考虑一个形式为$x=az+b$，它很容易求逆,得到 $z=\frac{1}{a}(x-b)$ 。

但是，线性变换在复合下是封闭的——一系列线性变换等效于一个整体线性变换。此外,高斯分布的线性变换仍然是高斯分布。因此,即使我们有许多这样的线性变换,我们也只会得到一个高斯分布。

问题是，我们能否在保持线性变换可逆性的同时,允许额外的灵活性,以便结果分布是非高斯的呢？

这个问题的一个解决方案是由一种称为RealNVP^[1] 的归一化流模型给出,它是“real-valued non-volume preserving”的缩写。

想法是将潜在变量向量z分成两部分 $z=(z _ {A},z _ {B})$,使得如果z的维度是 $D _ {i}$ 而 $Z _ {A}$ 的维度是d,那么 $z _ {B}$ 的维度是 $D-d _ {n}$ 。

我们同样将输出向量 $x=(x _ {A},x _ {B})$ 划分,其中 $x _ {A}$ 的维度为d。

而对于输出向量的第一部分,我们简单地复制输入: $x _ {A}=z _ {A}$ ，$x _ {B}$ 的维度为 $D-d _ {\circ}$

向量的第二部分经过线性变换,但现在线性变换中的系数由 $Z _ {A}$ 的非线性函数给出：

$$x _ {B}=exp(s(z _ {A},w))\odot z _ {B}+b(z _ {A},w)$$

其中 $s(z _ {A},w)$ 和 $b(z _ {A},w)$ 是神经网络的实值输出,指数函数确保乘法项为非负。这里表示涉及两个向量逐元素乘法的Hadamard积。

由于使用了神经网络函数, $x$ 的值可以是非常灵活的函数。

整体变换也很容易可逆：给定一个 $x=(x _ {A},x _ {B})$的值，我们首先计算$z _ {A}=x _ {A}$ ，然后有$z _ {B}=exp(-s(z _ {A},w))\odot(x _ {B}-b(z _ {A},w))$。

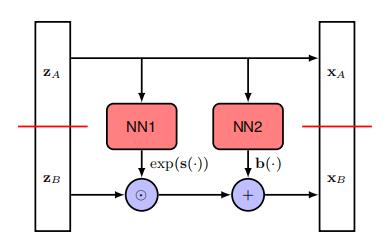
值得注意的是， $s(z;w)$ 和 $b(z;w)$ 无需可逆。

现在考虑雅可比矩阵及其行列式。我们可以将雅可比矩阵分成块,对应于z和x的划分,得到:

$$
J=\begin{bmatrix}\frac{\partial z_A}{\partial x_A}&\frac{\partial z_A}{\partial x_B}\\ \frac{\partial z_B}{\partial x_A}&\frac{\partial z_B}{\partial x_B}\end{bmatrix}=\begin{bmatrix}I _ {d}&0\\ \frac{\partial z _ {B}}{\partial x _ {A}}&diag(exp(-s))\end{bmatrix}
$$

我们不在乎左下角的值，因为它是一个下三角矩阵，行列式直接是主对角线元素的乘积。因此,雅可比行列式简单地由 $exp(-s(z _ {A},w))$ 的元素乘积给出。

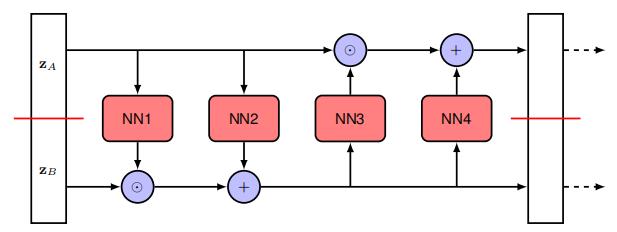
这种方法的一个明显限制是 $z _ {A}$ 的值不受变换的影响。这很容易通过添加另一层来解决,在该层中 $z _ {A}$ 和 $z _ {B}$ 的角色被反转。然后可以重复这种双层结构多次。

整体训练过程涉及创建数据点的mini-batches。对于形式为 $\mathcal{N}(z|0,I)$ 的潜在分布,对数密度简单地是 $-||z||^{2}/2$,仅差一个加性常数。
$$
\ln(\frac{1}{\sqrt{2\pi}}\exp(-\frac{z^2}{2}))=\ln(\frac{1}{\sqrt{2\pi}})+\frac{-||z||^2}{2}
$$
另外，Real NVP模型中会使用BatchNorm，这也会使得多一些变换行列式。

RealNVP 模型属于一类称为耦合流（Coupling Flows）的正则化流,其中线性变换$x _ {B}=exp(s(z _ {A},w))\odot z _ {B}+b(z _ {A},w)$被更一般的形式$x _ {B}=h(z _ {B},g(z _ {A},w))$ 所替代。

其中 $h(z _ {B}g)$ 是一个关于 $z _ {B}$ 的函数，对于任何给定的g值都是可逆的,称为耦合函数。函数 $g(z _ {A},w)$ 称为条件器（conditioner）,通常由神经网络表示。

笔者也动手实现了realnvp的代码：

class CouplingLayer(nn.Module):
    def __init__(self, input_dim, hidden_dim, mask_type='even'):
        super().__init__()
        self.input_dim = input_dim
        self.mask = torch.zeros(input_dim, device=device)
        if mask_type == 'even':
            self.mask[::2] = 1  # Condition on even, transform odd
        else: # 'odd'
            self.mask[1::2] = 1 # Condition on odd, transform even
        
        self.s_net = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, input_dim),
            nn.Tanh() # To stabilize: limits scale factor somewhat
        )
        self.t_net = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, input_dim)
        )

    def forward(self, x):
        """ x -> z (inverse transformation for density estimation) """
        # x_masked conditions the transformation
        x_masked = x * self.mask 
        s = self.s_net(x_masked) * (1 - self.mask) # s applies only to non-masked part
        t = self.t_net(x_masked) * (1 - self.mask) # t applies only to non-masked part
        
        # Inverse affine transformation: z_B = (x_B - t) * exp(-s)
        z = (x * (1 - self.mask) - t) * torch.exp(-s) + x_masked
        
        # Log determinant of Jacobian: sum of -s for the transformed part
        log_det_jacobian = (-s).sum(dim=1)
        return z, log_det_jacobian

    def inverse(self, z):
        """ z -> x (forward transformation for sampling) """
        # z_masked conditions the transformation
        z_masked = z * self.mask
        s = self.s_net(z_masked) * (1 - self.mask)
        t = self.t_net(z_masked) * (1 - self.mask)
        
        # Affine transformation: x_B = z_B * exp(s) + t
        x = (z * (1 - self.mask)) * torch.exp(s) + t + z_masked
        
        # For generation, we also need log_det_jacobian (or its inverse) if we were to calc prob of x
        # but here we just need x. The log_det_jacobian for x = f(z) would be sum(s).
        log_det_jacobian_inv = s.sum(dim=1) # log |det J_f| = -log|det J_g|
        return x, log_det_jacobian_inv


class RealNVP(nn.Module):
    def __init__(self, num_layers, input_dim, hidden_dim):
        super().__init__()
        self.layers = nn.ModuleList()
        for i in range(num_layers):
            mask_type = 'even' if i % 2 == 0 else 'odd'
            self.layers.append(CouplingLayer(input_dim, hidden_dim, mask_type))
        
        # Base distribution (e.g., standard normal)
        self.base_distribution = torch.distributions.Normal(
            torch.zeros(input_dim, device=device), 
            torch.ones(input_dim, device=device)
        )

    def forward(self, x): # For density estimation x -> z
        log_det_jacobian_sum = 0
        z = x
        for layer in reversed(self.layers): # Inverse direction for density
            z, log_det_jacobian = layer.forward(z) # This is g(x)
            log_det_jacobian_sum += log_det_jacobian
        return z, log_det_jacobian_sum

    def inverse(self, z): # For sampling z -> x
        # log_det_jacobian_inv_sum = 0 # Not typically needed for just sampling
        x = z
        for layer in self.layers: # Forward direction for sampling
            x, _ = layer.inverse(x) # This is f(z)
            # log_det_jacobian_inv_sum += log_det_jacobian_inv # If we needed prob(x) from f(z)
        return x
    def log_prob(self, x):
        z, log_det_jacobian_sum = self.forward(x)
        # log p(x) = log p(z) + log |det J_g|
        log_likelihood_z = self.base_distribution.log_prob(z).sum(dim=1)
        return log_likelihood_z + log_det_jacobian_sum

    def sample(self, num_samples):
        z = self.base_distribution.sample((num_samples,))
        x_generated = self.inverse(z)
        return x_generated

值得注意的是，图像是离散数据，而Realnvp是针对连续数据，我们需要做一些处理才可能成功运行。

一个最简单的方法是使用autoencoder，并用潜在向量来训练realnvp。神经网络是连续的，它可以把离散的图像转为连续的潜在向量，且能通过decoder很好地重建回离散图像。

另一个方法是反量化（Dequantization）。一个最简单的反量化是对每个离散值添加一个范围在$ [0, 1)$之间的随机噪声，并将其映射为0~1之间，比如使用sigmoid等。

另一种做法是变分反量化，在flow++^[2]中提出（flow++还引入了自注意力），即将反量化过程本身也变成了一个需要学习和优化的模型。

class VariationalDequantization(Dequantization):
    
    def __init__(self, var_flows, alpha=1e-5):
        """
        Inputs: 
            var_flows - A list of flow transformations to use for modeling q(u|x)
            alpha - Small constant, see Dequantization for details
        """
        super().__init__(alpha=alpha)
        self.flows = nn.ModuleList(var_flows)
        
    def dequant(self, z, ldj):
        z = z.to(torch.float32)
        img = (z / 255.0) * 2 - 1 # We condition the flows on x, i.e. the original image
        
        # Prior of u is a uniform distribution as before
        # As most flow transformations are defined on [-infinity,+infinity], we apply an inverse sigmoid first.
        deq_noise = torch.rand_like(z).detach()
        deq_noise, ldj = self.sigmoid(deq_noise, ldj, reverse=True)
        for flow in self.flows:
            deq_noise, ldj = flow(deq_noise, ldj, reverse=False, orig_img=img)
        deq_noise, ldj = self.sigmoid(deq_noise, ldj, reverse=False)
        
        # After the flows, apply u as in standard dequantization
        z = (z + deq_noise) / 256.0
        ldj -= np.log(256.0) * np.prod(z.shape[1:])
        return z, ldj

处理前： 可以发现训练不一定能成功，有时会坍塌。

处理后：

OpenAI在RealNVP改进得到了Glow模型^[3]。

其核心是可逆1x1卷积层，其中巧妙地利用了LU分解。

即任意矩阵都可以分解为$W=PLU$，则$log|det(W)|=\sum log|diag(U)|$

故Glow中采用的是，先随机生成一个正交矩阵，然后做LU分解，得到P,L,U。

固定P，固定U的对角线的正负号，约束L为对角线全1的下三角阵，U为上三角阵，优化训练L,U的其余参数。

from scipy import linalg as la

class InvConv2dLU(nn.Module):
    def __init__(self, in_channel):
        super().__init__()

        weight = np.random.randn(in_channel, in_channel)
        q, _ = la.qr(weight)
        w_p, w_l, w_u = la.lu(q.astype(np.float32)) # PLU分解
        w_s = np.diag(w_u) # 计算U对角线元素
        w_u = np.triu(w_u, 1) # 约束U为上三角阵（不包括对角线）
        u_mask = np.triu(np.ones_like(w_u), 1) # 全1上三角阵
        l_mask = u_mask.T # 全1下三角阵

        w_p = torch.from_numpy(w_p)
        w_l = torch.from_numpy(w_l)
        w_s = torch.from_numpy(w_s)
        w_u = torch.from_numpy(w_u)

        self.register_buffer("w_p", w_p)
        self.register_buffer("u_mask", torch.from_numpy(u_mask))
        self.register_buffer("l_mask", torch.from_numpy(l_mask))
        self.register_buffer("s_sign", torch.sign(w_s)) # U对角线的正负号
        self.register_buffer("l_eye", torch.eye(l_mask.shape[0])) # 单位阵
        self.w_l = nn.Parameter(w_l) # 可学习参数：L的下三角元素
        self.w_s = nn.Parameter(logabs(w_s)) # 可学习参数：U的对角元素的对数值
        self.w_u = nn.Parameter(w_u) # 可学习参数：U的上三角元素

        self.weight = (
            self.w_p # P为固定值
            @ (self.w_l * self.l_mask + self.l_eye) # 下三角阵L对角线元素全为1，其余参数可学习
            @ ((self.w_u * self.u_mask) + torch.diag(self.s_sign * torch.exp(self.w_s))) # 上三角阵U对角线的正负号固定，其余参数可学习
        )
        self.weight = self.weight.unsqueeze(2).unsqueeze(3)

    def forward(self, input):
        _, _, height, width = input.shape
        out = F.conv2d(input, self.weight)
        logdet = height * width * torch.sum(self.w_s)
        return out, logdet

    def reverse(self, output):
        return F.conv2d(output, self.weight.squeeze().inverse().unsqueeze(2).unsqueeze(3))

自回归流（Autoregressive Flows）

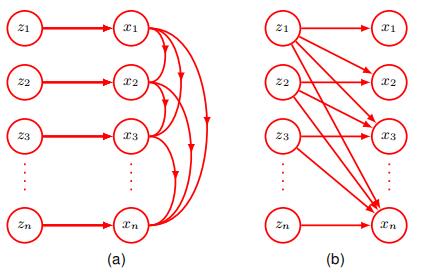
一个与正则化流相关的公式可以从注意到一组变量的联合分布总是可以表示为每个变量的条件分布的乘积来推导。我们可以不失一般性地写出：

$$p(x _ {1},…,x _ {D})=\prod _ {i=1}^{D}p(x _ {i}|x _ {1:i-1})$$

其中 $x _ {1:i-1}$ 表示 $x _ {1},…,x _ {i-10}$ 这种分解可用于构建一类称为掩码式自回归流(masked autoregressive flow，MAF)的归一化流,其定义为：

$$x _ {i}=h(z _ {i},g _ {i}(x _ {1:i-1},w _ {i}))$$

这里 $h(z _ {i},\cdot)$ 是耦合函数,其被选择为相对于易于 $z _ {i}$ 求逆的,而g是条件器,通常由深度神经网络表示。掩码式指的是使用单个神经网络来实现上式以及一个二元掩码，该掩码强制网络权重的子集为零以实现自回归约束。

在这种情况下,用于评估似然函数的逆向计算需要给出：

$z _ {i}=h^{-1}(x _ {i},g _ {i}(x _ {1:i-1},w _ {i}))$

因为上式中用于评估的各个函数 $z _ {1},…,z _ {D}$ 可以并行评估，因此可以在现代硬件上高效执行。

与上式对应的雅可比矩阵的元素 $\partial z _ {i}/\partial x _ {j}$ 它们形成一个上三角矩阵,其行列式由对角元素的乘积给出,因此也可以高效评估。

然而,从这个模型中进行采样必须通过评估$x _ {i}=h(z _ {i},g _ {i}(x _ {1:i-1},w _ {i}))$来完成,这本质上是有序的，因此很慢。

为了避免这种低效的采样，可以定义一个逆自回归流（inverse autoregressive flows，IAF）给出 ：

$$x _ {i}=h(z _ {i},\tilde{g} _ {i}(z _ {1:i-1},w _ {i}))$$

现在采样就更快了。

然而，其逆函数也还是具有序列性。

$$z _ {i}=h^{-1}(x _ {i},\tilde{g} _ {i}(z _ {1:i-1},w _ {i}))$$

连续流（Continuous Flow）

神经微分方程（Neural differential equations）

深度网络具有很深的层数是很有用。

所以，我们可以探索神经网络达到无限层数的极限会发生什么。

考虑一个残差网络,其中每一层的处理生成的输出由输入向量与输入向量的某些参数化非线性函数相加给出:

$$z^{(t+1)}=z^{(t)}+f(z^{(t)},w)$$

其中 $t=1,…,T$ 标记网络中的层。

为了简便，我们在每一层都使用了相同的函数,并共享参数向量w。

在极限情况下,隐藏单元激活向量成为连续变量的函数 $z(t)$,我们可以将此向量在网络中的演变表示为一个微分方程:

$$\frac{dz(t)}{dt}=f(z(t),w)$$

中的公式被称为一个神经常微分方程或神经 ODE。

如果我们用向量 $z(0)$ 表示网络的输入,那么输出 $z(T)$ 是通过积分微分方程获得的：

$$z(T)=\int _ {0}^{T}f(z(t),w)dt$$

这个积分可以使用标准的数值积分包来评估。求解微分方程的最简单方法是欧拉前向积分方法,它对应于表达式$z^{(t+1)}=z^{(t)}+f(z^{(t)},w)$。

在实践中,更强大的数值积分算法可以自适应地调整它们的函数评估以实现。特别是,它们可以自适应地选择的值,这些值通常不是均匀分布的。

神经ODE反向传播

我们得到了神经ODE的形式，那么如何通过优化损失函数来确定w的值呢？假设我们有一个数据集,其中包含输入向量 $z(0)$ 的值,以及相关的输出目标向量和损失函数 $L(\cdot)$,该函数取决于输出向量 $z(T)$。

一种方法可能是使用自动微分来对ODE求解器在正向传递期间执行的所有操作进行微分。尽管这很直接，但从内存角度来看代价很高,并且在控制数值误差方面不是最优的。

相反,Chen等人^[4]将ODE求解器视为一个黑盒,并使用一种称为伴随敏感性方法的技术,这可以看作是显式反向传播的连续类比。

为了将反向传播应用于神经ODE,我们定义一个称为伴随的量,其定义为：

$$a(t)=\frac{dL}{dz(t)}$$

我们看到 $a(T)$ 对应于损失关于输出向量的常规导数。伴随子满足其自身的微分方程,该方程为：

$$\frac{da(t)}{dt}=-a(t)^{T}\nabla _ {z}f(z(t),w)$$

证明：
$$
\begin{align}
a(t)&=\frac{dL}{dz(t)}\\
a(t+\delta t)&\approx\frac{dL}{dz(t+\delta t)}\\
z(t+\delta t)&\approx z(t)+f(z(t),w)\delta t\\
\therefore \frac{\partial L}{\partial z(t)}&=\frac{\partial L}{\partial z(t+\delta t)}\frac{\partial z(t+\delta t)}{\partial z(t)}\\
a(t)&=a(t+\delta t)(I+\nabla_zf()\delta t)
\end{align}
$$

这是一个微积分链式法则的连续版本。这可以通过从 $a(T)$ 开始反向积分来求解,这同样可以使用黑盒ODE求解器来完成。

关于网络参数的导数。当一个参数值在网络的多个连接中共享时,总导数由每个连接的导数之和形成。

对于我们的神经ODE,其中相同的参数向量 w在整个网络中共享,这个求和变成了对的积分,其形式为：

$$\nabla _ {w}L=-\int _ {0}^{T}a(t)^{T}\nabla _ {w}f(z(t),w)dt$$

$\nabla _ {z}f$ 和 $\nabla _ {w}f$ 可以使用自动微分高效地计算。注意,上述结果同样适用于一个更通用的神经网络函数 $f(z(t),t,w)$ 它在除了通过 $z(t)$ 隐式依赖之外,还对有显式依赖。

使用伴随方法训练的神经ODE相比于传统层状网络的一个优点是,不需要存储前向传播的中间结果,因此内存成本是恒定的。

此外，神经 ODE可以自然地处理连续时间数据,其中观测值在任意时间发生。如果误差函数 L 取决于除输出值之外的 $z(t)$ 的值,那么需要多次运行反向模型求解器,每次运行对应一对连续的输出,以便将单个解分解为多个连续解,从而访问中间状态。

神经ODE flows

神经ODE定义了一种高度灵活的从输入向量 $z(0)$ 到输出向量 $z(T)$ 的变换,该变换以微分方程的形式给出：

$$\frac{dz(t)}{dt}=f(z(t),w)$$

如果我们定义一个关于输入向量 $p(z(0))$ 的基础分布,那么神经ODE 会将其随时间向前传播,为每个的值给出一个分布 $p(z(t))$,从而得到一个关于输出向量 $p(z(T))$ 的分布。

Chen^[4]表明,对于神经ODE,密度的变换可以通过积分一个由下式给出的微分方程来评估：

$$\frac{\partial~lnp(z(t))}{\partial t}=-Tr(\frac{\partial f}{\partial z(t)})$$

其中 $\partial f/\partial z$ 表示雅可比矩阵,其元素为 $\partial f _ {i}/\partial z _ {jc}$。

作者使用的是泰勒级数展开式等来证明。

我们也可以进一步展开为：
$$
\frac{\partial~lnp(z(t))}{\partial t}=-\nabla\cdot f=-Tr(\frac{\partial f}{\partial z(t)})
$$

证明：

根据连续性方程（其密度的局部变化率等于流入该点的通量（flux）的负散度，也叫传输方程）：
$$
\frac{\partial p(z)}{\partial t}+\nabla\cdot (p(z)f)=0
$$
根据向量微积分的乘法法则：
$$
\nabla\cdot (pf)=\nabla p (f)+p(\nabla \cdot f)
$$
根据多元链式法则，
$$
\frac{\partial~lnp(z(t))}{\partial t}=\frac{1}{p}(\frac{\partial p}{\partial t}+(\nabla p)f)
$$
把二者结合起来有：
$$
\frac{\partial~lnp(z(t))}{\partial t}=-\nabla\cdot f
$$
而一个向量场的散度在数学上等于其雅可比矩阵的迹。

这个积分可以使用标准的ODE 求解器来执行。同样,可以从基础密度 $p(z(0))$ 中采样,该分布被选择为一个简单的分布,例如高斯分布,并通过再次使用ODE 求解器积分将值传播到输出。

由此产生的框架被称为一个连续归一化流。连续归一化流可以使用用于神经ODE的伴随敏感性方法进行训练,这可以看作是反向传播的连续时间等价物。

由于涉及雅可比矩阵的迹而不是使用行列式，因此它可能看起来在计算上更高效。
通常,计算一个 $D\times D$ 矩阵的行列式需要 $\mathcal{O}(D^{3})$ 次操作,而计算迹只需要 $\mathcal{O}(D)$ 次操作。

然而,如果行列式是下三角形的,如在许多归一化流的形式中,那么行列式是主对角线项的乘积,因此也涉及 $\mathcal{O}(D)$ 次操作。由于计算雅可比矩阵的各个元素需要单独的前向传播,而前向传播本身需要 $\mathcal{O}(D)$ 次操作,因此计算迹或行列式(对于下三角矩阵)总共需要 $\mathcal{O}(D^{2})$ 次操作。

然而,通过使用 Hutchinson 迹估计器^[5],可以将计算迹的成本降低到 $\mathcal{O}(D)$。

该估计器对于一个矩阵A采用以下形式 ：

$$Tr(A)=\mathbb{E} _ {\epsilon}[\epsilon^{T}A\epsilon]$$

其中是$\epsilon$一个均值为零、协方差为一的随机向量,例如,高斯 $\mathcal{N}(0,I)$。

我们不需要计算整个矩阵A，就能得到$\epsilon^{T}A\epsilon$的值。

具体而言，

（1）计算神经网络的前向传播f(z)

（2）计算f(z)和$\epsilon$的点积，得到$L=\epsilon\cdot f(z)$

（3）执行反向传播，计算L关于z的梯度，则梯度为$\epsilon^T\frac{\partial f}{\partial z}$

（4）最后计算梯度和$\epsilon$的点积，$(\epsilon^T\frac{\partial f}{\partial z})\cdot \epsilon$

然后我们可以使用有限数量的样本来近似迹,形式为：

$$Tr(A)\approx\frac{1}{M}\sum _ {m=1}^{M}\epsilon _ {m}^{T}A\epsilon _ {m}$$

这里其实牵扯到一个叫雅可比向量积 (Jacobian-Vector Product，JVP)的概念，即一个行向量 v^T 与一个雅可比矩阵 J 的乘积

流匹配（Flow Matching）

该方法^[6]于2022年提出。

Flow代表继续延续连续归一化流（CNF）的核心。即一个类似流动的过程，或者说基于连续性方程/传输方程的思想。

Matching类似之前博客曾提过的分数匹配。

而与前面的流模型不同，流匹配是一种在训练过程中不需要求解ODE来训练的方法。

类似分数匹配，我们之间对向量场进行构建回归目标，（我们继续延续流模型中的符号，部分符号会和流匹配论文中常用的符号略有不同）：
$$
\mathcal{L} _ {FM}=E _ {t\sim U(0,1),X_t\sim p_t}||f_t(X_t,t)-f^\theta_t(X_t,t)||^2
$$
然而我们并不知道$p_t$和真实向量场$f$，所以就有了条件流匹配的出现。

条件流匹配（Conditional Flow Matching）

CFM 的核心思想是选择一个额外变量 z 和一个条件概率路径$p(x\mid t,z)$。
$$
\mathcal{L} _ {CFM}=E _ {t\sim U(0,1),X_t\sim p_t,z\sim q(z)}||f_t(X_t,t;z)-f_t^\theta(X_t,t)||^2
$$
Lipman 等人^[6]证明了$\mathcal{L} _ {FM}$和$\mathcal{L} _ {CFM}$只相差一个与$\theta$无关的常数，二者梯度相等。证明其实很简单，把期望内的括号展开分离即可。

对于z，我们可以只考虑$x_1$，定义$\mu(z,t)=tx_1$，$\sigma(z,t)=t\sigma _ {const}-t+1$，则
$$
\begin{align}
p _ {t}(\mathbf{x} | \mathbf{z}) &= \mathcal{N}\left( \mathbf{x} | t \mathbf{x}_1, (t \sigma _ {const} - t + 1)^2 \mathbf{I} \right) \\
f(\mathbf{x}, t ; \mathbf{z}) &= \frac{ \mathbf{x}_1 - (1 - \sigma _ {const}) \mathbf{x} }{ 1 - (1 - \sigma _ {const}) t }
\end{align}
$$
这也就是原始的CFM^[6]，也叫锥形高斯路径（Conical Gaussian paths）。

对于z，我们也可以将$x_0$和$x_1$联合起来考虑，定义$\mu(z,t)=(1-t)x_0+tx_1$，$\sigma(z,t)=\sigma _ {const}$，则
$$
\begin{align}
p _ {t}(\mathbf{x} | \mathbf{z}) &= \mathcal{N}\left( \mathbf{x} | t \mathbf{x}_1+(1-t)x_0, \sigma _ {const}^2 \mathbf{I} \right) \\
f(\mathbf{x}, t ; \mathbf{z}) &= x_1-x_0
\end{align}
$$
这也就是independent CFM（iCFM)^[7]，也叫线性插值。 它也与最优传输（Optimal Transport）有关，正如其论文标题所述。

完整流程：

1.采样 t∼Uniform(0,1)

2.采样 z∼q(z)

3.计算$\mu_z$和$\sigma_t(z)$

4.计算$x_t\sim\mathcal{N}(x\mid\mu(z,t),\sigma(z,t))$

5.计算向量场$f$

6.计算损失

7.更新参数

MeanFlow

我们直接跳到最新的研究。由何恺明组提出的《Mean Flows for One-step Generative Modeling》^[8]。

回顾一下前文：

$$\frac{dz(t)}{dt}=f(z(t),w)$$

这实际上代表着瞬时速度。

然而瞬时速度并不是直接指向数据点，所以无法一步生成，而要一步生成需要平均速度才能实现。

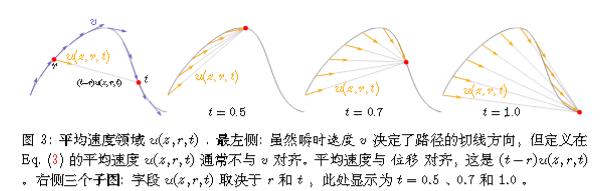
展开来说，前文的flow matching尽管使用的是直线插值，但是实际上是线性加噪而非线性去噪。导致我们无法一步生成。

我们也可以使用一些形象的方法来解释。

当只有一个力源的情况下，它的场线是直线（左图和中图），这与我们的加噪相似，我们也可以类似PFGM，将这一过程理解为数据点被力场推着走向目标位置。

然而，我们不止一个力源，所以最终场（右图）并不是一条直线。

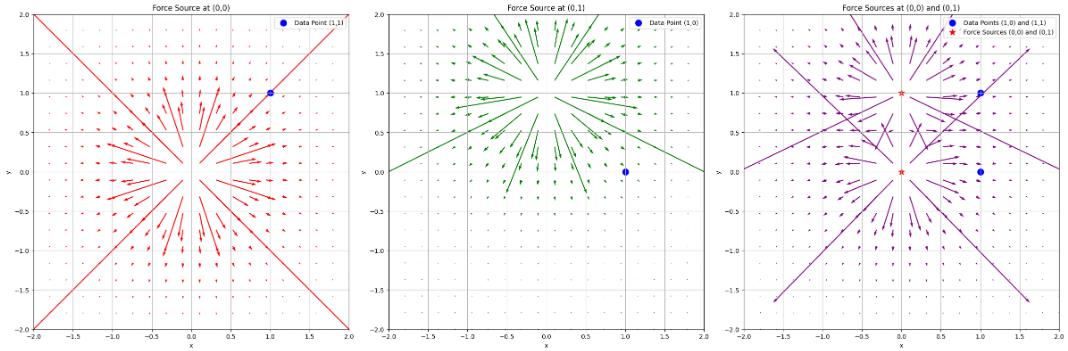
我们也很难去设计一种力，使得合并后的最终场是直线形式。

面对天体运动，与其我们引入复杂的本轮均轮来完善地心说，更好的方法是直接引入日心说。

故MeanFlow另起炉灶，虽然继续使用同样的力源，但不继续做文章，而是使用了平均速度。

我们延用论文中的符号。

瞬时速度：

$$
\frac{dz(t)}{dt}=v(z(t),w)
$$

而平均速度场 u 和瞬时速度场 v 有以下关系：

$$(t - r)u(z_t, r, t) = \int_r^t v(z _ {\tau}, \tau) d\tau$$

$$\frac{d}{dt} (t - r)u(z_t, r, t) = \frac{d}{dt} \int_r^t v(z _ {\tau}, \tau) d\tau \implies u(z_t, r, t) + (t - r)\frac{d}{dt}u(z_t, r, t) = v(z_t, t)$$

若我们想利用平均速度一步就能得到结果, 则就需要平均速度场满足

$$
\underbrace{u(z_t, r, t)} _ {\text{average vel.}} = \underbrace{v(z_t, t)} _ {\text{instant. vel.}} - \underbrace{(t - r)\frac{d}{dt}u(z_t, r, t)} _ {\text{time derivative}}
$$

对于最后一项有：

$$
\frac{d}{dt}u(z_t, r, t) = \frac{dz_t}{dt}\partial_z u + \frac{dr}{dt}\partial_r u + \frac{dt}{dt}\partial_t u
$$

其中：

$$
\frac{dz_t}{dt} = v(z_t, t), \quad \frac{dr}{dt} = 0, \quad \frac{dt}{dt} = 1
$$

在上文的 Hutchinson 迹估计器中，JVP已见其威力，我们不需要计算整个雅克比矩阵A，就能得到矩阵的迹。同样地我们在这里也可以对上式使用。

最终设定损失函数：
$$
\mathcal{L}(\theta) = \mathbb{E}\left[ || u_\theta(z_t, r, t) - \text{sg}(u _ {\text{tgt}}) ||^2_2 \right]
$$

其中

$$
u _ {\text{tgt}} = v(z_t, t) - (t-r)(v(z_t, t)\partial_z u_\theta + \partial_t u_\theta)
$$
在这里我们会使用sg(stop gradient)，因为我们并不需要它的导数，也避免了再去求高阶导数。

参考资料

本文参考了多篇公开资料（博客、代码等等）^{[9][10][11][12][13][14][15][16]}和一些教科书^[17]和李宏毅的课程^[18]。

1. Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio. Density estimation using Real NVP ↩
2. Ho, J., Chen, X., Srinivas, A., Duan, Y., and Abbeel. Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design ↩
3. Diederik P. Kingma, Prafulla Dhariwal.Glow: Generative Flow with Invertible 1x1 Convolutions ↩
4. Ricky T. Q. Chen. Neural Ordinary Differential Equations ↩
5. Will Grathwohl, Ricky T. Q. Chen, Jesse Bettencourt, Ilya Sutskever, David Duvenaud. FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models ↩
6. Yaron Lipman. FLOW MATCHING FOR GENERATIVE MODELING。 ↩
7. Tong, A., Malkin, N. Improving and generalizing flow-based generative models with minibatch optimal transport. ↩
8. Zhengyang Geng, Mingyang Deng, Xingjian Bai, J. Zico Kolter, Kaiming He. Mean Flows for One-step Generative Modeling ↩
9. 生成扩散模型漫谈（三十）：从瞬时速度到平均速度. https://kexue.fm/archives/10958 ↩
10. Flow Matching: Matching flows instead of scores. https://jmtomczak.github.io/blog/18/18_fm.html ↩
11. Yaron Lipman. Flow Matching Guide and Code ↩
12. A Visual Dive into Conditional Flow Matching. https://dl.heeere.com/conditional-flow-matching/blog/conditional-flow-matching/#d-footnote-9 ↩
13. Deep Learning Course at the University of Amsterdam (MSc AI), Fall 2023. https://github.com/phlippe/uvadlc_notebooks ↩
14. 流模型(Flow-based Model). https://0809zheng.github.io/2022/05/01/flow.html ↩
15. Diederik P. Kingma, Tim Salimans, Rafal Jozefowicz, Xi Chen, Ilya Sutskever, Max Welling. Improving Variational Inference with Inverse Autoregressive Flow ↩
16. George Papamakarios, Theo Pavlakou, Iain Murray. Masked Autoregressive Flow for Density Estimation ↩
17. PRML ↩
18. 李宏毅的Flow-based Generative Model课程 ↩