经典的GNN被淘汰了吗？

各种GNN结构层出不穷，比如Graphformer等transformer模型。不禁产生一个疑问：经典的GNN被淘汰了吗？

以下这几篇正是对这一疑问的驳斥。

正好对应图领域中的链接预测、节点分类、图层次三大任务。其中后两篇均为Yuankai Luo的作品。

（NIPS 2023） Evaluating Graph Neural Networks for Link Prediction

（NIP2 2024 ）Classic GNNs are Strong Baselines: Reassessing GNNs for Node Classification

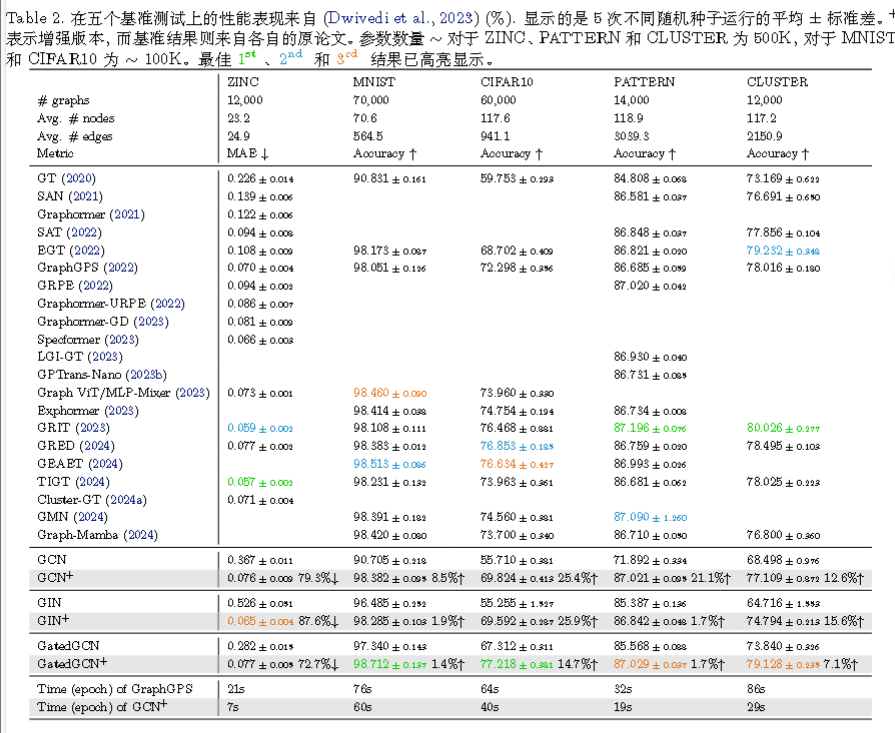
（ICML 2025 ）Unlocking the Potential of Classic GNNs for Graph-level Tasks: Simple Architectures Meet Excellence

节点预测

（1）作者注意到，多个模型的性能被低估。对于某些方法，如标准 GNNs，
这是由于调参不当所致。一旦进行适当的调参，它们甚至可以在某些指标上达到最佳整体性能。

（2）大多数模型的排序指标标准差往往较高。例如，MRR的标准差在 Cora、Citeseer 和 Pubmed 上分别高达 8.82 、8.96 和 7.75 。此外，在 ogbl-ddi数据集上，Hits@20 的标准差甚至达到了 10.47 和 15.56。

高方差意味着模型性能不稳定。这使得比较不同方法的结果变得困难，因为真实性能存在于更大的值域内。这进一步增加了复制模型性能的复杂性，因为即使与报告结果存在较大差异，也可能仍处于方差范围内。

也导致作者可能会取偏高的作为结果，而难以体现模型的平均性能。

（3）惯用的AUC 并不是链接预测的合适指标。

改进评估方案

现有的链接预测评估过程是将一个正例与一组 K 随机选择的负例进行排名。所有正例都使用相同的 K 个负例（ogbl-citation2 除外，它每个正例使用 1000 个）。

然而这种评估方法会有以下问题：

问题1：非个性化的负例。

现有的评估情景对所有正例使用相同的负例集合（ogbl-citation2除外）。这种策略，称为全局负采样，不是通常追求的目标。相反，我们通常更感兴趣的是预测特定结点将发生的链接。例如，一个连接朋友用户的社交网络。

在这种情景下，我们可能有兴趣为用户推荐新朋友 u 。这需要学习一个分类器 f ，它为链接存在的概率进行赋值。在评估此任务时，我们希望将 u 连接到现有朋友的链接排在那些不连接的链接之上。

例如，如果 u 与 a 是朋友但不是 b 的朋友，我们希望 f (u, a) > f (u, b) 。然而，现有的评估情景并未明确测试这一点。而是将一个真实样本 (u, a) 与一个可能无关的负例进行比较，例如 (c, d) 。这与此类图上链接预测的实际应用不符。

问题 2: 易判负例（Easy Negative Samples）。

现有评估情景中随机选取负例进行使用。然而，考虑到大多数图的规模
较大，随机采样的负例很可能选择两个彼此无关的结点。这类结点对
分类起来轻而易举。

作者进一步表明，即使在较小的数据集中，这一问题依然存在。

新方法：

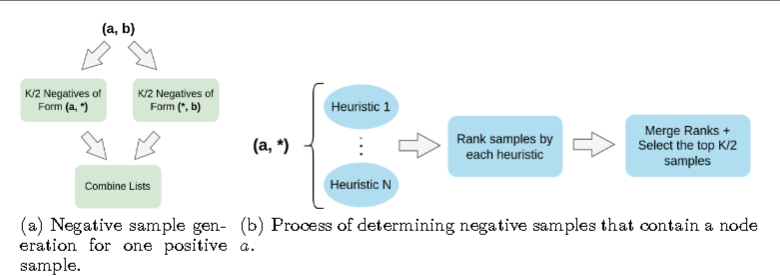
作者的策略 HeaRT 通过以下方式解决这些挑战：

(a) 为每个样本个性化负例

(b) 使用启发式方法选择难负例。这使得负例能够与每个正例直接相关，同时又不失挑战性。

节点分类

具体采用的数据集有：

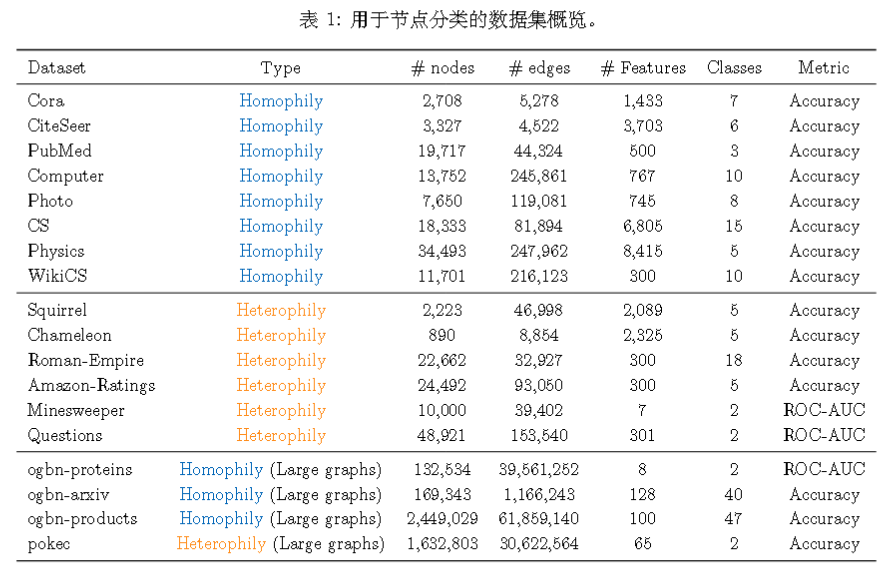
在同质图上：

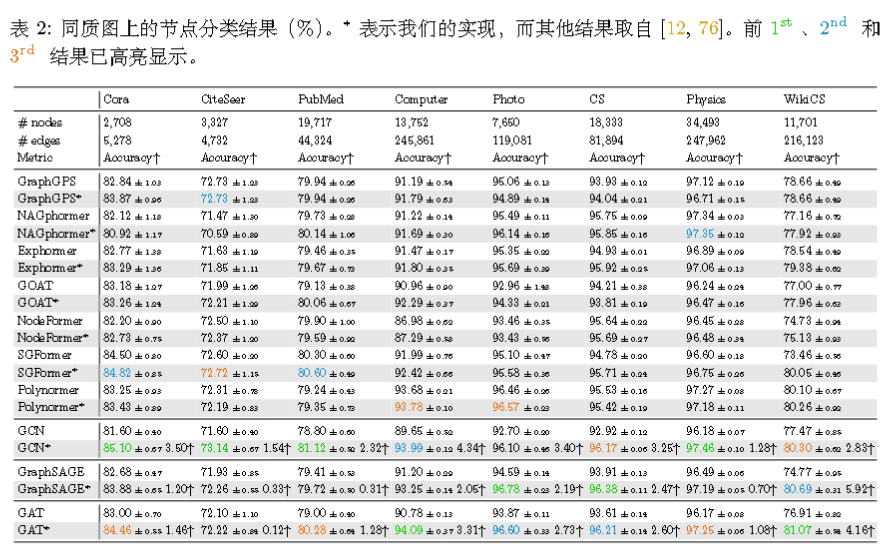
经典 GNN 仅需对超参数进行微调，便能在同质图上的节点分类任务中表现出极强的竞争力，在许多情况下甚至超越了最先进的图Transformer！

在异质图上：

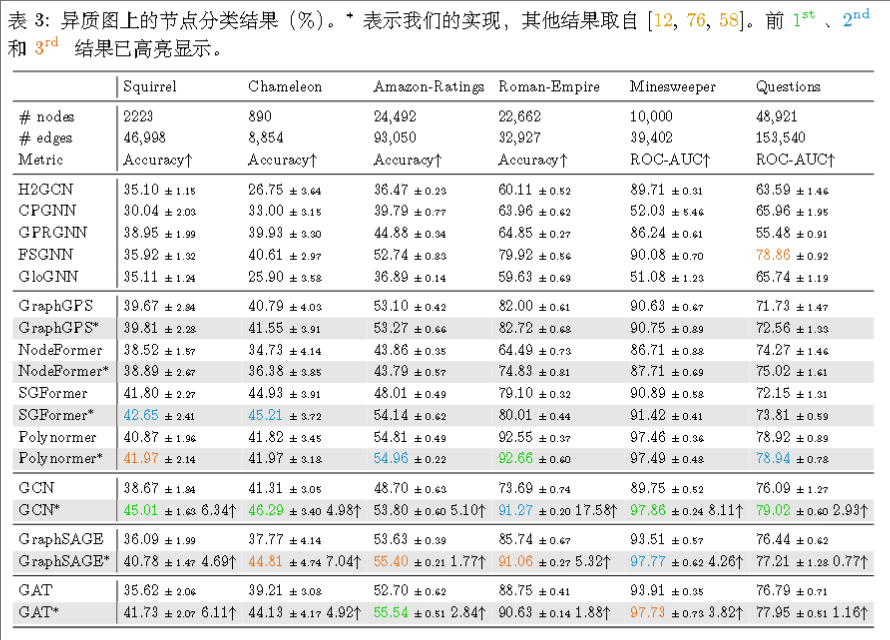
传统 GNN依旧在异质图中是强有力的竞争者。

在大规模图上：

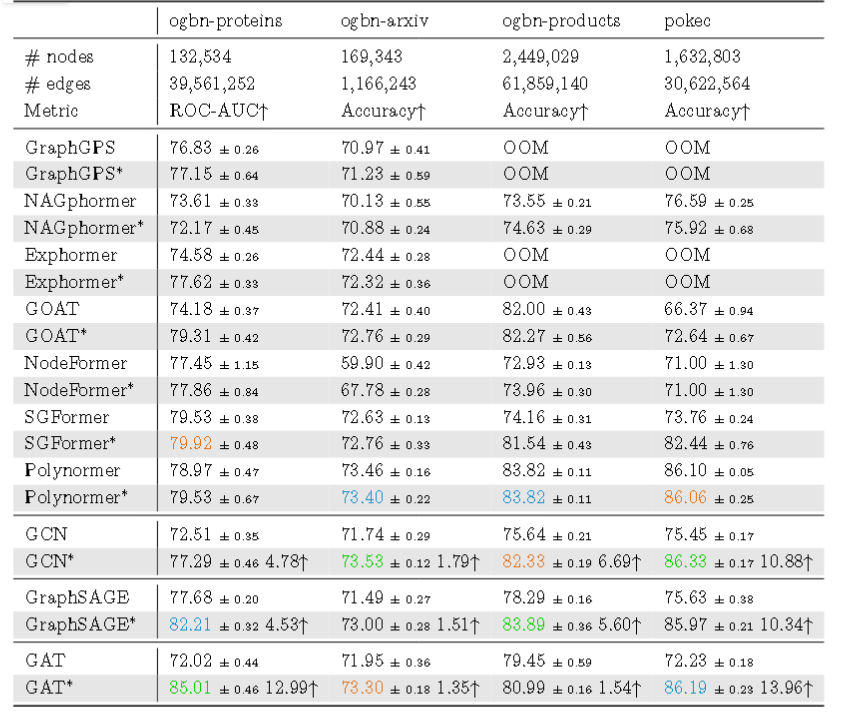
传统 GNN在这些大规模图数据集上取得了最佳结果，无论是同质性还是异质性图，均超越了最先进的图 Transformer。这表明消息传递在大
规模图上学习结点表示仍然非常有效。

图层次

作者并不是使用传统的GNN，而是提出了GNN+，即GNN整合了六种流行技术边特征集成、Normalization、Dropout、残差连接、FFN以及位置编码。

边特征集成

$$
h_v^l=\sigma(\sum_{u\in N(v)\cup{v}}\frac{1}{\sqrt{\hat d_u\hat d_v}}h_u^{l-1}W^l)
$$

边特征集成即：
$$
h_v^l=\sigma(\sum_{u\in N(v)\cup{v}}\frac{1}{\sqrt{\hat d_u\hat d_v}}h_u^{l-1}W^l+e_{uv}W^l_e)
$$
其中$e_{uv}、W^l_e$分别为u和v之间的特征向量和第$l$层的可训练权重矩阵。

位置编码

作者采用的是随机游走结构编码（RWSE）。

之前的博客曾介绍过相关的Graph Neural Networks with Learnable Structural and Positional Representations，在这里不再赘述。
$$
x_v=[x_v||x_v^{RWSE}]W_{PE}
$$