DDPM加速

正如DDIM作者在其论文中所写，“从 DDPM 中采样 50k 个 32×32 大小的图像大约需要 20 小时，但在 Nvidia 2080 Ti GPU 上从 GAN 中完成这一操作不到一分钟。”

DDPM等扩散模型的慢速度一直被诟病。

在这篇博客中，将介绍一部分的加速模型。

DDIM

ICLR 2021。2010年10月发表。

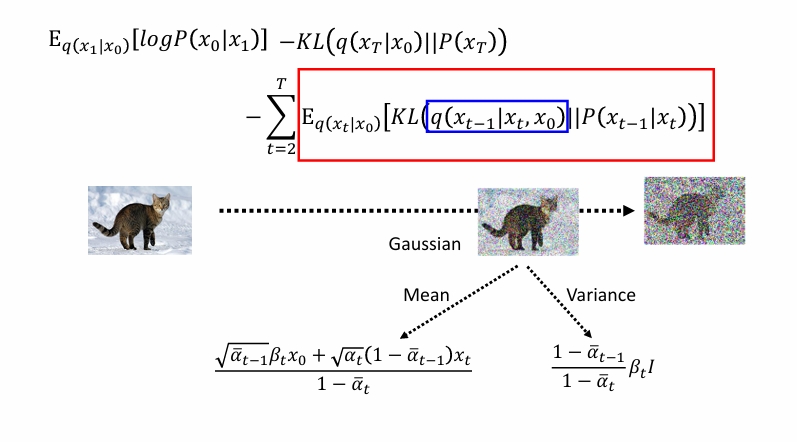
让我们回忆一下DDPM。

延续符号：

$\bar \alpha_t=\alpha_1\alpha_2…\alpha_t$

$a_t=1-\beta_t$

$\tilde \beta_t=\frac{1-\bar \alpha _ {t-1}}{1-\bar \alpha _ {t}}\beta_t$

有
$$
\begin{align}
x_0&=\frac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}
\\
q(x _ {t-1}\mid x_t,x_0)&=N(\frac{\sqrt{\alpha _ {t-1}}\beta_tx_0+\sqrt{\alpha_t}(1-\bar\alpha _ {t-1})x_t}{1-\bar\alpha_t},\frac{1-\bar \alpha _ {t-1}}{1-\bar \alpha _ {t}}\beta_tI)
\\&=N(\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon\right),\frac{1-\bar \alpha _ {t-1}}{1-\bar \alpha _ {t}}\beta_tI)
\end{align}
$$

我们将方差分离开，（或者叫做重参数化），即：

$$
\begin{align}
q(x _ {t-1}\mid x_t,x_0)&=\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon\right)+\sqrt{\tilde \beta_t}N(0,1)
\\&=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{1}{\sqrt{\alpha_t}}\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon+\sqrt{\tilde \beta_t}N(0,1)
\\&=\frac{\sqrt{\bar\alpha _ {t-1}}}{\sqrt{\bar\alpha _ {t}}} x_t
-\frac{1}{\sqrt{\alpha_t}}\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon+\sqrt{\tilde \beta_t}N(0,1)
\\&=\sqrt{\bar\alpha _ {t-1}} \frac{x_t-\sqrt{1-\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}
+\sqrt{\bar\alpha _ {t-1}} \frac{\sqrt{1-\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}
-\frac{1}{\sqrt{\alpha_t}}\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon
+\sqrt{\tilde \beta_t}N(0,1)
\\&=\sqrt{\bar\alpha _ {t-1}} x_0
+\frac{1}{\sqrt{\alpha_t}}\frac{1-\bar\alpha_t-(1-\alpha_t)}{\sqrt{1-\bar\alpha_t}}\epsilon
+\sqrt{\tilde \beta_t}N(0,1)
\\&=\sqrt{\bar\alpha _ {t-1}} x_0
+\frac{1}{\sqrt{\alpha_t}}\frac{\alpha_t-\bar\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon
+\sqrt{\tilde \beta_t}N(0,1)
\\&=\sqrt{\bar\alpha _ {t-1}} x_0
+\frac{1}{\sqrt{\alpha_t}}\frac{\alpha_t(1-\bar\alpha _ {t-1})}{\sqrt{1-\bar\alpha_t}}\epsilon
+\sqrt{\tilde \beta_t}N(0,1)
\\&=\sqrt{\bar\alpha _ {t-1}} x_0
+\sqrt{1-\alpha _ {t-1}-\tilde\beta_t}\epsilon
+\sqrt{\tilde \beta_t}N(0,1)
\end{align}
$$

我们干脆把$\sqrt{\tilde\beta_t}$定义为超参数$\sigma_t$，即$\sigma_t^2=\eta \tilde\beta_t$。当$\eta=0$为DDIM，当$\eta=1$时为DDPM。

方差为0有个好处，就是它变为了确定性的，我们就可以像GAN那样进行插值。

虽然我们破坏了DDPM的$q(x _ {t-1}\mid x_t,x_0)$中原有的性质，但是我们并未破坏$q(x _ t\mid x_0)$的性质。这从推导过程中是可以看出来的。所以这样做也是可行的。

IDDPM

2021年2月发表。

《Improved Denoising Diffusion Probabilistic Models》

我们同样对方差进行操作，不过我们让神经网络去学习它。我们预测一个参数v，并令：
$$
\sigma_t^2(x,t)=exp(vlog\beta_t+(1-v)log\tilde\beta_t)
$$
同时我们也在损失函数中加入与这个项相关的。

TDPM

ICLR 2023。2022年2月发表。

《Truncated Diffusion Probabilistic Models and Diffusion-based Adversarial Auto-Encoders》

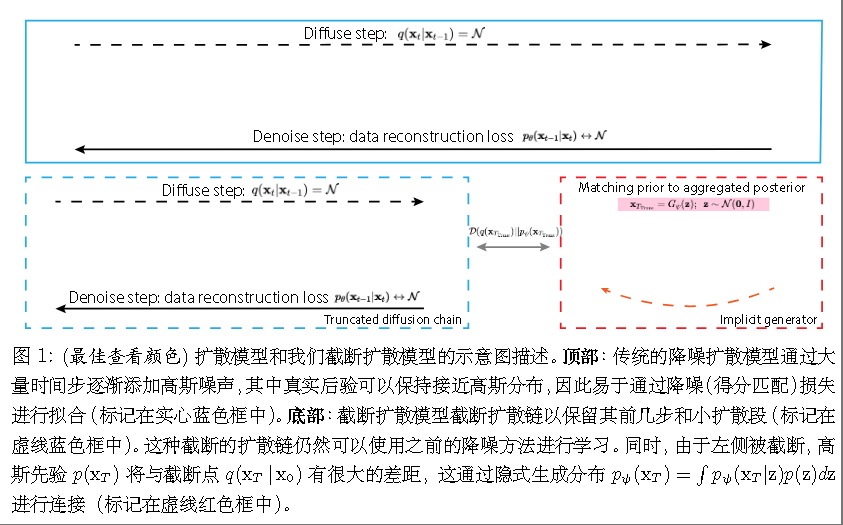
作者选择不是被扩散到纯高斯噪声 xT，而是只扩散到一个中间的、噪声程度较低的时刻$T _ {trunc}$。

且$q(x _ {trunc}\mid x_0)$仍然遵循标准的扩散定义:
$$
X _ {trunc}=\sqrt{\bar\alpha}x_0+\sqrt{1-\bar\alpha}\epsilon
$$
但是$q(X _ {trunc})$不再是高斯分布，所以作者使用GAN去生成它。

渐进式蒸馏

另一个常用于加速/量化的策略是知识蒸馏。

这篇正是这样做的。

ICLR2022，2022二月发表。

《Progressive Distillation for Fast Sampling of Diffusion Models》

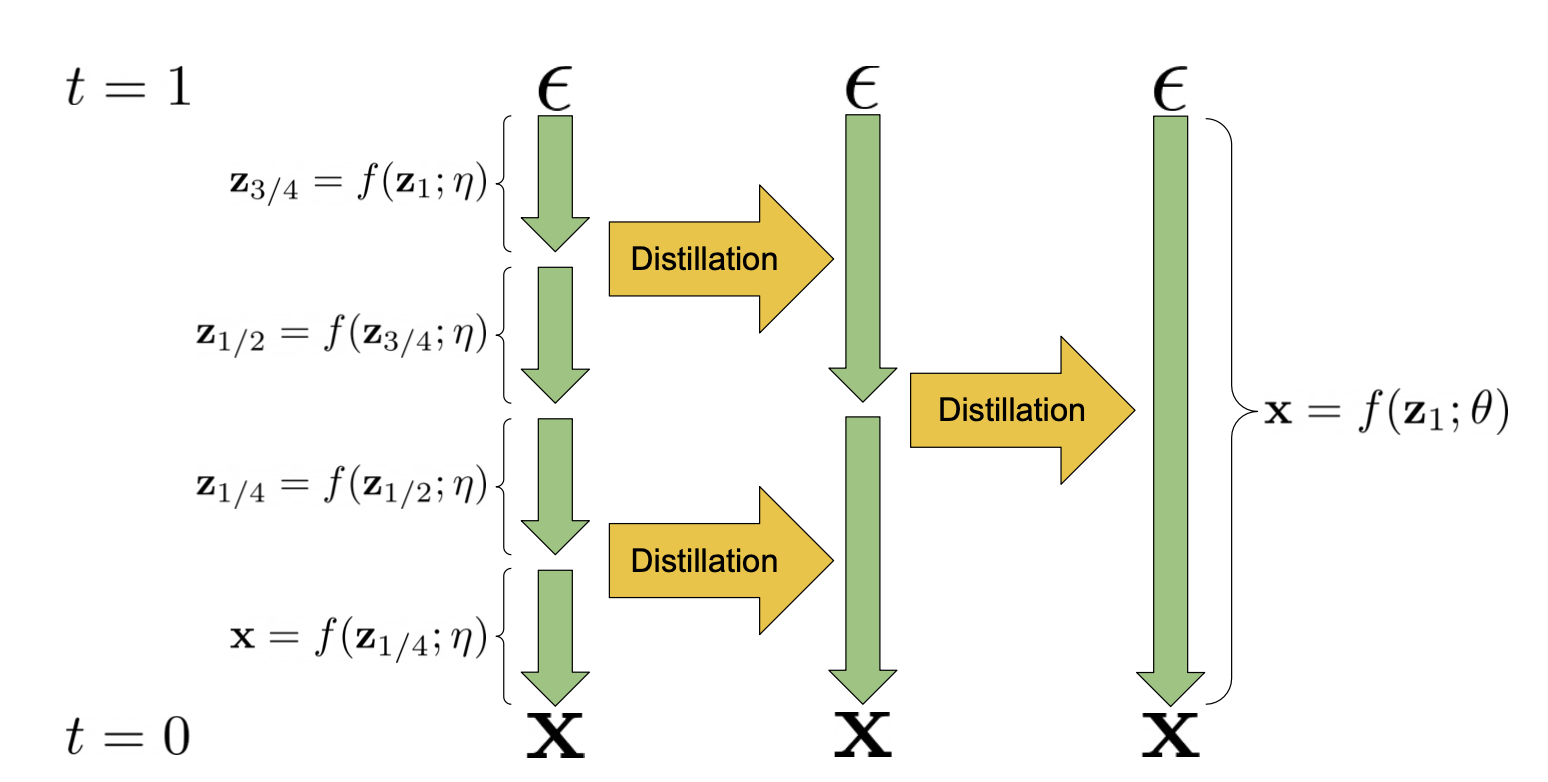
使用学生模型去学习如何用一步来模拟教师模型多步（通常是两步）的去噪效果。

DPMSolver

Neurips 2022。2022年6月发表。

DPMSolver由于涉及到更高维度，比如从ODE/SDE的角度上俯瞰问题。

并非主要是模型上的改进，故我们不在这里做过多描述。

具体而言，扩散模型可以写成ODE的形式，但是标准的一阶 ODE 求解器（如欧拉法，注意与上一章中的欧拉-丸山法作区分）在求解上述 ODE 时，为了保证精度，通常需要非常小的步长，导致采样步数很多（例如 1000 步）。

DPMSolver的核心思想来源于观察到扩散模型中的 ODE 具有特殊的半线性结构 (semi-linear structure)。

我们简要介绍一下一阶DPMSolver。

欧拉法

欧拉法是最简单、最基础的 ODE 数值求解器。它的核心思想是用当前点的导数（即切线斜率）来线性外推到下一个点。

假设我们知道在时刻$t_i$的样本$x_i$，以及此时的导数$F(x_i,t_i)$。如果我们想前进一个时间步长$h=t _ {i+1}-t_i$：
$$
x _ {i+1}\approx x_i+hF(x_i,t_i)
$$

一阶 DPMSolver

扩散模型的 ODE 通常可以被看作或转化为 $dx/d\lambda=LinearPart(\lambda,x)+NonLinearPart(\lambda,\epsilon_\theta(x,\lambda))$，其中$\lambda_t=log(\bar\alpha_t/\sigma_t^2)$。

我们定义为：

$$
\frac{d{x}}{d\lambda} = F(\lambda){x} + G(\lambda){\epsilon}_\theta({x}, \lambda)
$$

其中：

• ${x}$ 是当前的样本。
• $\lambda$ 是重新参数化后的时间或噪声水平。
• $F(\lambda){x}$ 是关于 ${x}$ 的线性部分。
• $G(\lambda){\epsilon} _ \theta({x}, \lambda)$ 是非线性部分，其中 ${\epsilon} _ \theta({x}, \lambda)$ 是神经网络对噪声的预测。

在从当前时间 $\lambda_i$ 到下一个时间 $\lambda _ {i+1}$ 的一个小子区间内，我们将非线性相关的部分（即神经网络的输出 ${\epsilon} _ \theta({x}, \lambda)$）近似为在该区间开始时的值，即 $\epsilon _ {\theta,i} = {\epsilon}_\theta({x}_i, \lambda _ i)$，并将其视为常数。

这样，ODE 变为：

$$
\frac{d{x}}{d\lambda} = F(\lambda){x} + G(\lambda){\epsilon} _ {\theta,i}
$$

这是一个关于 ${x}$ 的一阶线性非齐次微分方程。

代入定义的：
$$
\begin{align}
F(\lambda)&=\frac{1}{2}\frac{dlog\sigma_\lambda^2}{d\lambda}
\\
G(\lambda)&=-\frac{\sigma_\lambda}{2\alpha_\lambda}\frac{dlog\sigma_\lambda^2}{d\lambda}
\end{align}
$$

可得更新公式为：
$$
x _ {i+1}=\frac{\sigma(\lambda _ {i+1})}{\sigma(\lambda _ {i})}x_I-\sigma(\lambda _ {i+1})(e^k-1)\epsilon_\theta(x_i,\lambda_i))
$$

Consistency Models

一作Yang Song。Ilya Sutskever通讯。

ICML 2023,2023 5月发表。

Consistency Models 的基石是概率流常微分方程 (Probability Flow Ordinary Differential Equation, PF ODE)。在扩散模型的连续时间视角下，存在一个 PF ODE，其轨迹可以将任何数据点平滑地转换到不同噪声水平 t 下的含噪版本，反之亦然。

”一致性“定义为：

对于任何沿着同一条轨迹的数据点$(x_t,t)$和$(x _ {t’},t’)$，通过一致性函数$f$的映射，都应该得到相同的轨迹起点，即原始数据$x_0$。
$$
f(x_t,t)=x_0\quad \text{for all}\quad t\in[\epsilon,T]
$$
其中$\epsilon$是一个接近于0很小的正数，T是总的扩散时间。

对于同一轨迹上的任意两个点，我们期望：
$$
f(x_t,t)=f(x _ {t’},t’)
$$
边界条件：

对于任何$f$,都有$f(x_\epsilon，\epsilon)=x_\epsilon$

故$f$可设为：
$$
f_\theta (x,t)=
\begin{cases}x\quad &t=\epsilon
\\
F_\theta(x,t)\quad &t\in(\epsilon ,T]
\end{cases}
$$

或$f_\theta(x,t)=c _ {skip}(t)x+c _ {out}F_\theta(x,t)$，其中c是可微函数，且$c _ {skip}(\epsilon)=1$和$c _ {out}(\epsilon)=0$。

有两种训练方法：

（1）一致性蒸馏（Consistency Distillation ，CD）

它依赖于一个已经训练好的扩散模型（教师模型）。一致性蒸馏损失定义为:
$$
\begin{aligned}
\mathcal{L}^N_\text{CD} (\theta, \theta^-; \phi) &= \mathbb{E}
[\lambda(t_n)d(f_\theta(x _ {t _ {n+1}}, t _ {n+1}), f _ {\theta^-}(\hat{x}^\phi _ {t_n}, t_n)]
\end{aligned}
$$
其中
$x\sim p _ {data}$，$n \sim \mathcal{U}[1, N-1]$，$x _ {t _ {n+1}}\sim N(x;t _ {n+1}^2I)$。
$\hat{x}^\phi _ {t_n} = {x} _ {t _ {n+1}} - (t_n - t _ {n+1}) \Phi(x _ {t _ {n+1}}, t _ {n+1}; \phi)$，$\Phi$是在执行一步欧拉法，$\phi$代表教师模型。

$\theta^-$是$\theta$ 的移动平均。
d是距离函数满足$d(x,y)\ge 0$ ，$d(x,y)=0$ 仅当$x=y$。论文中考虑L1、L2、LPIPS损失。
$\lambda$是正权重函数，论文定义为1。

作者还发现设置stopgrad效果会更好，且稳定训练过程。

即$\theta^-\leftarrow stopgrad(\mu\theta^-+(1-\mu)\theta)$。

(2)一致性训练(Consistency Training)

在前面的CD中，使用预训练的score model来近似真实的分数函数$\nabla logp_t(x)$。而
$$
\nabla logp_t(x_t)=-E\left[\frac{x_t-x}{t^2}\mid x_t\right]
$$

若 $x \sim p _ {\text{data}}(x)$, $x_t \sim \mathcal{N}(x; t^2 I)$, $p_t(x_t) = p _ {\text{data}}(x) \otimes \mathcal{N}(0, t^2 I)$，或者写作$p_t(x_t)=\int p _ {\text{data}}(x) \mathcal{N}(x_t;x, t^2 I)dx$。则有 $\nabla \log p_t(x_t) = -\mathbb{E}[\frac{x_t - x}{t^2} | x_t]$。

证明：根据 $p_t(x_t)$的定义, 我们有$\nabla \log p_t(x_t) = \nabla _ {x_t} \log \int p _ {\text{data}}(x) p(x_t | x) dx$, 其中 $p(x_t | x) = \mathcal{N}(x_t; x, t^2 I)$.
$$
\begin{align}
\nabla \log p_t(x_t) &= \frac{\int p_{\text{data}}(x) \nabla_{x_t} p(x_t | x) dx}{\int p_{\text{data}}(x) p(x_t | x) dx} \\
&= \frac{\int p_{\text{data}}(x) p(x_t | x) \nabla_{x_t} \log p(x_t | x) dx}{\int p_{\text{data}}(x) p(x_t | x) dx} \\
&= \frac{\int p_{\text{data}}(x) p(x_t | x) \nabla_{x_t} \log p(x_t | x) dx}{p_t(x_t)} \\
&= \int \frac{p_{\text{data}}(x) p(x_t | x)}{p_t(x_t)} \nabla_{x_t} \log p(x_t | x) dx \\
&\stackrel{(Bayes’rule)}{=} \int p(x | x_t) \nabla_{x_t} \log p(x_t | x) dx \\
&= \mathbb{E}[\nabla_{x_t} \log p(x_t | x) | x_t] \\
&= -\mathbb{E}\left[\frac{x_t - x}{t^2} | x_t\right]
\end{align}
$$

损失函数变为：
$$
\mathcal{L}^N_\text{CT} (\theta, \theta^-; \phi) = \mathbb{E}
[\lambda(t_n)d(f_\theta({x} + t_{n+1} {z},;t_{n+1}), f_{\theta^-}({x} + t_n {z},;t_n)]
\text{ where }{z} \in \mathcal{N}({0}, {I})
$$