朗之万动力学和diffusion

朗之万动力学是一种描述粒子在流体中运动的物理模型，它考虑了两种主要的力：

耗散力 (Dissipative Force)：也称为摩擦力或阻尼力。这种力与粒子的速度成正比，方向相反，模拟了粒子在运动时由于与周围流体分子碰撞而受到的能量损失。数学上通常表示为 −γv，其中 γ 是阻尼系数，v 是粒子的速度。
随机力 (Random Force)：也称为噪声项。这种力模拟了流体中分子对粒子的随机碰撞，这些碰撞是无规则且快速变化的。它通常被建模为一个均值为零的高斯白噪声，其强度与系统的温度和阻尼系数有关。这个力是系统能量的来源，使得粒子能够克服耗散力并进行持续的随机运动（布朗运动）。

粗略而言，朗之万动力学采样依赖于分数（score）函数。而Tweedie公式提供了估计分数函数的方法。

故我们先介绍Tweedie公式和一些基本概念。

Tweedie公式和DDPM

Tweedie公式为$E[x\mid y]=y+\sigma^2\nabla log p(y)$。其中$\nabla logp(y)$被称为分数（score）。

证明：

$$
\begin{align}
p(y)&=\int p(y\mid x)p(x)dx
\\\nabla p(y)&=\nabla \int p(y\mid x)p(x)dx
\\&= \int \nabla p(y\mid x)p(x)dx
\end{align}
$$
由$p(y\mid x ) \propto exp(-\frac{1}{2\sigma^2}||y-x||^2)$得，$\nabla p(y\mid x)=-\frac{1}{\sigma^2}(y-x)p(y\mid x)$

故
$$
\begin{align}
\nabla p(y)&= \int -\frac{1}{\sigma^2}(y-x)p(y\mid x)p(x)dx
\\&=-\frac{1}{\sigma^2}y\int p(y\mid x)p(x)dx+\frac{1}{\sigma^2}\int p(y\mid x)xp(x)dx
\\&=-\frac{1}{\sigma^2}yp(y)+\frac{1}{\sigma^2}E[x\mid y]p(y)
\end{align}
$$
而$\nabla log p(y)=\frac{\nabla p(y)}{p(y)}$，两边同除$p(y)$即可得到。

沿用DDPM的$q(x_t\mid x_0) = \mathcal{N}(x _ {t} ; \sqrt{\bar\alpha_t}x_0, \left(1 - \bar\alpha_t\right)\textbf{I})$，由Tweedie公式有：
$$
\begin{align}
\mathbb{E}\left[\mu _ {x_t}\mid x_t\right] = x_t + (1 - \bar\alpha_t)\nabla _ {x_t}\log p(x_t)
\\
\therefore \sqrt{\bar\alpha_t}x_0 = x_t + (1 - \bar\alpha_t)\nabla\log p(x_t)
\\
\therefore x_0 = \frac{x_t + (1 - \bar\alpha_t)\nabla\log p(x_t)}{\sqrt{\bar\alpha_t}}
\end{align}
$$
对比DDPM中的$x _ 0=\frac{x _ t - \sqrt{1 - \bar \alpha _ t} \epsilon _ 0}{\sqrt{\bar\alpha _ t}}$，可以发现$\nabla \log p(x _ t) = -\frac{1}{ \sqrt{1 - \bar \alpha _ t}}\epsilon _ 0$。

DDPM其实也是基于分数函数来去噪。

去噪分数匹配

我们不妨考虑以下分布，被称为能量函数：
$$
\begin{align}
p _ {\boldsymbol{\theta}}(\boldsymbol{x}) = \frac{1}{Z _ {\boldsymbol{\theta}}}e^{-f _ {\boldsymbol{\theta}}(\boldsymbol{x})}
\end{align}
$$
我们可以通过神经网络来对学习$\nabla \log p(x)$：
$$
\begin{align}
\nabla _ {x} \log p _ {\theta}(x)
&= \nabla _ {x}\log(\frac{1}{Z _ {\theta}}e^{-f _ {\theta}(x)})
\\
&= \nabla _ {x}\log\frac{1}{Z _ {\theta}} + \nabla _ {x}\log e^{-f _ {\theta}(x)}\\
&= -\nabla _ {x} f _ {\theta}(x)\\
&= s _ {\theta}(x)
\end{align}
$$
具体而言，即我们可以使用神经网络f进行建模，通过任意计算其负梯度来查询分数；或者，更常见的是，我们可以直接使用神经网络对s进行建模。
$$
\mathbb{E} _ {p(x)}\left[\left\lVert s _ {\theta}(x) - \nabla\log p({x})\right\rVert_2^2\right]
$$
但接下来的一个难点是，我们很难知道$\nabla\log p({x})$。

2005年Aapo Hyvarinen在他的《Estimation of Non-Normalized Statistical Models by Score Matching》中提出了：
$$
\mathbb{E} _ {p(x)}\left[tr(\nabla s_\theta(x) )+\frac{1}{2}\lVert s_\theta(x) \rVert^2\right]
$$
这种没有使用p的方法也被叫做Implicit Score Matching。但是这种方法随着应用场景的维度的升高，迹变得更加难求。

2010年Pascal Vincent在他的《A connection between score matching and denoising autoencoders》中提出了：
$$
\mathbb{E} _ {p(\tilde x,x)}\left[\frac{1}{2}\lVert s_\theta(\tilde x)- \frac{x-\tilde x}{\sigma^2}\rVert^2\right]
$$
其中$\tilde x$是加噪后的，或者是x是去噪后的。

逐渐有了现在去噪分数匹配的雏形，这样的形式就变得很好求了。

当我们知道score，那我们就可以进行采样了，下式被称为（未调整的）朗之万动力学采样（Unadjusted Langevin Algorithm）：
$$
{x} _ {i+1} \leftarrow {x}_i + c\nabla\log p({x}_i) + \sqrt{2c}{\epsilon},\quad i = 0, 1, …, K
$$
$\epsilon$为噪声，以实现更好的多样性。

朗之万动力学采样

这一章我们将证明上式是如何得到的。

一般的朗之万方程——对于一个质量为m的粒子，其位置为m，其动力学行为可以用以下随机微分方程描述：
$$
m\frac{d^2x}{dt^2}=F(x)-\gamma\frac{dx}{dt}+\eta(t)
$$
当粒子非常小或者阻尼非常大时，惯性项$m\frac{d^2x}{dt^2}$可以忽略不计，这被称为过阻尼朗之万动力学 (Overdamped Langevin Dynamics) 或布朗动力学。

我们考虑过阻尼朗之万动力学方程：

$$
\frac{d{x}(t)}{dt} = \frac{1}{\gamma}{F}({x}(t)) + \sqrt{\frac{2k_B T}{\gamma}}{\xi}(t)
$$

其中 ${F}({x}) = -\nabla U({x})$ 是由势能 $U({x})$ 产生的力，${\xi}(t)$ 是均值为0、协方差为 $\langle \xi_i(t) \xi_j(t’) \rangle = \delta _ {ij} \delta(t-t’)$ 的高斯白噪声。

为了简化，设定一个“有效的扩散系数” $D = k_B T / \gamma$，并将方程改写为：
$$
d{x}(t) = \frac{1}{\gamma}{F}({x}(t)) dt + \sqrt{2D} d{W}(t)
$$

我们依旧使用采样的目标分布是 $p({x}) \propto e^{-U({x})/(k_B T)}$，我们可以令 $U({x}) = -\log p({x})$ 并简写为：

$$
d{x}(t) = \nabla \log p({x}(t)) dt + \sqrt{2} d{W}(t)
$$

平衡态

福克-普朗克方程描述了在随机过程中概率密度函数 P(x,t) 如何随时间演化。我们采样的目标分布实际上是一个平稳解。

福克-普朗克方程描述了概率密度 $P({x}, t)$ 如何随时间演化。

对于一个由随机微分方程 $d{X}_t = {b}({X}_t)dt + \sqrt{2{D}({X}_t)}d{W}_t$ 描述的系统，其福克-普朗克方程为：
$$
\frac{\partial P({x}, t)}{\partial t} = -\sum_i \frac{\partial}{\partial x_i} [b_i({x}) P({x}, t)] + \sum _ {i,j} \frac{\partial^2}{\partial x_i \partial x_j} [D _ {ij}({x}) P({x}, t)]
$$
这里 ${b}({x})$ 是漂移向量，$D _ {ij}({x})$ 是扩散张量。

平稳解 $P_s({x})$ 是指不随时间变化的解，即 $\frac{\partial P_s({x})}{\partial t} = 0$。所以，我们需要解以下偏微分方程：
$$
-\sum_i \frac{\partial}{\partial x_i} [b_i({x}) P_s({x})] + \sum _ {i,j} \frac{\partial^2}{\partial x_i \partial x_j} [D _ {ij}({x}) P_s({x})] = 0
$$
这个方程通常可以写作 $\nabla \cdot [-{b}({x}) P_s({x}) + \nabla \cdot ({D}({x}) P_s({x}))] = 0$。更清晰的写法是定义概率流 (probability current) ${J}(P_s)$:
$$
J_k(P_s) = b_k({x}) P_s({x}) - \sum_j \frac{\partial}{\partial x_j} [D _ {kj}({x}) P_s({x})]
$$
则平稳的福克-普朗克方程变为散度为零：
$$
\sum_k \frac{\partial J_k(P_s)}{\partial x_k} = \nabla \cdot {J}(P_s) = 0
$$
寻找这个方程的通解可能非常困难，具体方法取决于漂移项 ${b}({x})$ 和扩散项 ${D}({x})$ 的形式以及边界条件。

为了简便，在这里我们只讨论一维情况。

在一维情况下，方程简化为：
$$
-\frac{d}{dx}[b(x) P_s(x)] + D \frac{d^2 P_s(x)}{dx^2} = 0
$$
这可以写成：
$$
\frac{d}{dx} \left[ -b(x) P_s(x) + D \frac{dP_s(x)}{dx} \right] = 0
$$
这意味着方括号内的项（即概率流 $J(x)$）是一个常数，记为 $J_0$：
$$
-b(x) P_s(x) + D \frac{dP_s(x)}{dx} = J_0
$$
对于大多数物理系统，尤其是在无限区域或者有反射边界的情况下，我们期望平稳态下没有净的概率流动，即 $J_0 = 0$。如果 $J_0 = 0$，则：
$$
D \frac{dP_s(x)}{dx} = b(x) P_s(x)
$$
这是一个可分离变量的一阶常微分方程：
$$
\frac{1}{P_s(x)} dP_s(x) = \frac{b(x)}{D} dx
$$
两边积分：
$$
\ln P_s(x) = \int \frac{b(x)}{D} dx + \text{const}
$$
所以，平稳解为：
$$
P_s(x) = A \exp\left(\int \frac{b(x)}{D} dx\right)
$$
其中 $A$ 是归一化常数，通过 $\int P_s(x) dx = 1$ 来确定。

这与我们假设的 $P_s({x}) \propto e^{-U({x})/(k_B T)}$ 形式类似。

离散化

欧拉-丸山法 (Euler-Maruyama method) 是离散化SDE最简单的方法之一。

考虑过阻尼朗之万方程的简化形式：

$$
d{x}(t) ={b}({x}(t)) dt + \sigma({x}(t)) d{W}(t)
$$

欧拉-丸山法的离散化更新规则如下：
给定当前状态 ${x}_k$ 在时间 $t_k$，下一个状态 ${x} _ {k+1}$ 在时间 $t _ {k+1} = t_k + \Delta t$ 可以近似为：
$$
{x} _ {k+1} ={x}_k +{b}({x}_k) \Delta t + \sigma({x}_k) \sqrt{\Delta t}{Z}_k
$$

其中：

$\Delta t$ 是离散的时间步长。
${Z}_k$ 是一个从标准多元正态分布（均值为0，协方差矩阵为单位矩阵 ${I}$）中抽取的随机向量。
$d{W}(t)$ 在离散时间步长 $\Delta t$ 内的增量 $\Delta{W}_k ={W}(t _ {k+1}) -{W}(t_k)$ 服从均值为0、协方差矩阵为 $\Delta t \cdot{I}$ 的正态分布。因此，$\Delta{W}_k$ 可以表示为 $\sqrt{\Delta t}{Z}_k$。

出现的问题

在p(x)较小的低密度区域，模型可能很难学习，从而导致效果不佳：

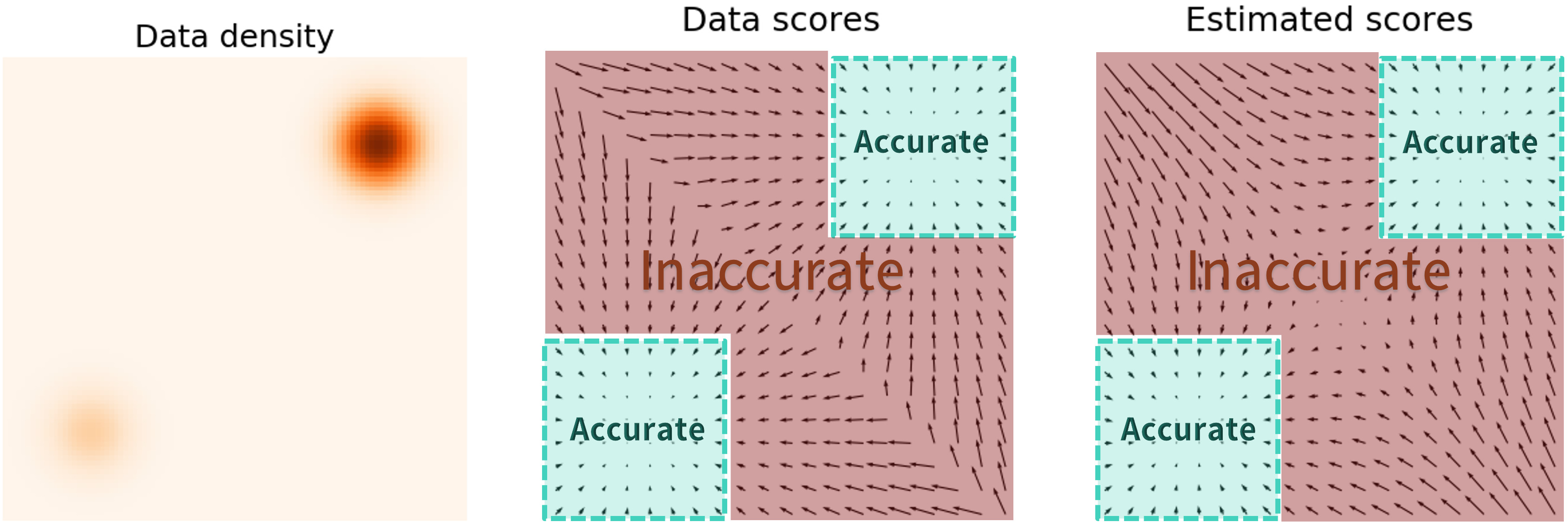
一个可行的办法是加大噪声以遍历更多的空间。

具有多重噪声扰动的生成模型

但我们如何选取噪声的大小呢？

yang song提出了同时使用多个尺度的噪声扰动。

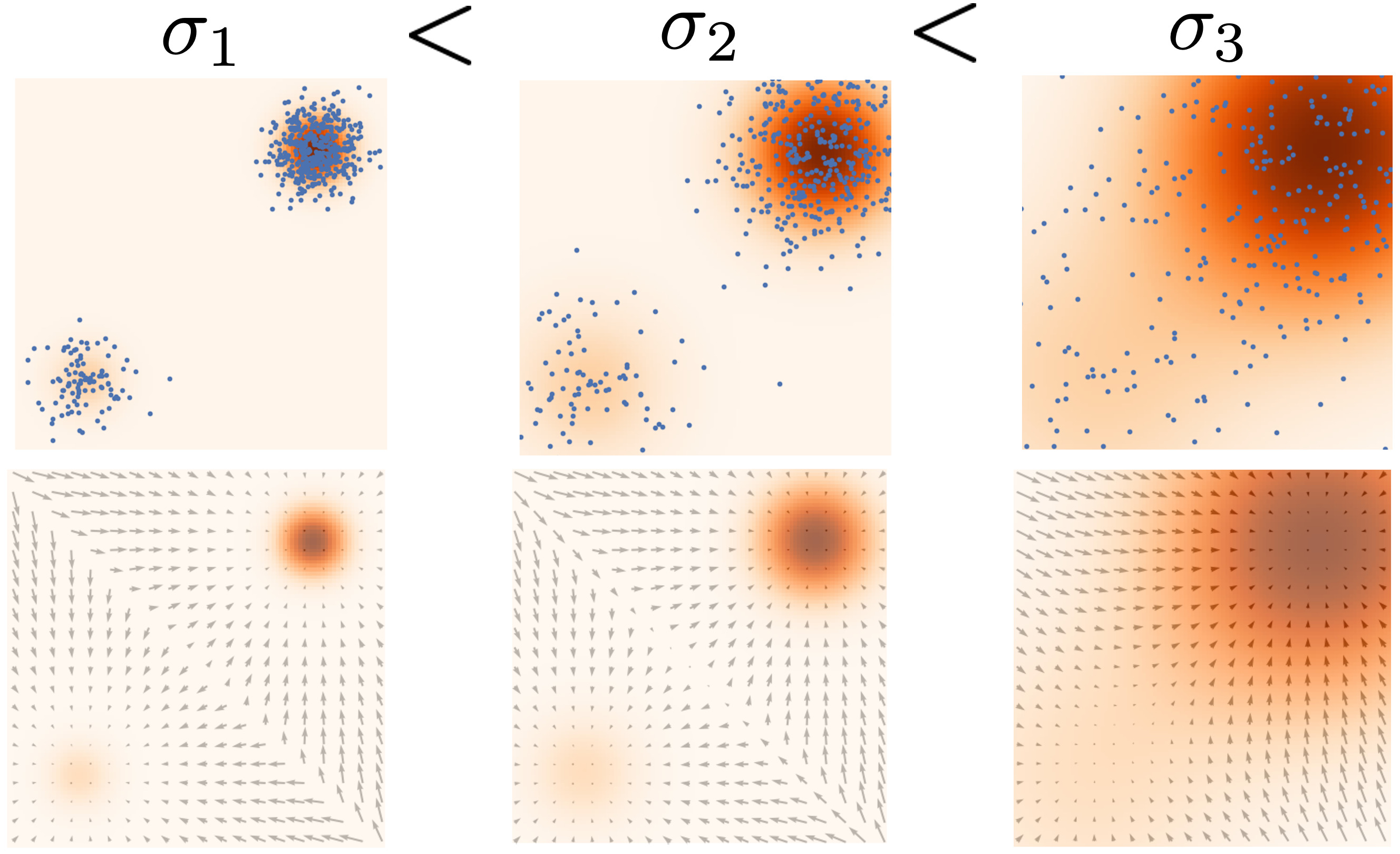
定义一个逐渐增加的方差$\sigma_1<\sigma_2<…<\sigma_L$，定义一个逐步扰动的数据分布序列：
$$
p _ {\sigma_t}({x}_t) = \int p({x})\mathcal{N}({x}_t; {x}, \sigma_t^2\textbf{I})d{x}
$$

使用神经网络同时学习所有噪声级别的得分函数：
$$
\underset{\arg\min}, \sum _ {t=1}^T\lambda(t)\mathbb{E} _ {p _ {\sigma_t}({x}_t)}\left[\left\lVert {s} _ ({x}, t) - \nabla\log p _ {\sigma_t}({x}_t)\right\rVert_2^2\right]
$$
其中通常定义$\lambda(i)=\sigma_i^2$。

使用退火朗之万动力学采样作为生成过程，其中通过依次对每个 $t=T,T-1…$运行朗之万动力学来生成样本。

song yang也提出来一些实用建议：