使用奇异值抵御标签噪声的免训练方法

上交东南大学出品（arxiv)。

事先观察

作者首先在干净的 CIFAR-100 数据集上训练一个成熟的分类器PRODEN，该分类器使用 ResNet-34作为骨干网络。

以预定义的概率 p 随机翻转每个样本的标签，生成具有不同程度标注噪声的数据集。并还强制实施一个约束，即每个样本至少保留一个标签。

对矩阵 W 和 W 进行奇异值分解（SVD），提取它们对应的奇异值Σ和Σ’以及右奇异酉矩阵，分别称为 V 和 V。然后，我们分析随着不准确度增加，不同权重的奇异值变化情况，结果如下图所示。

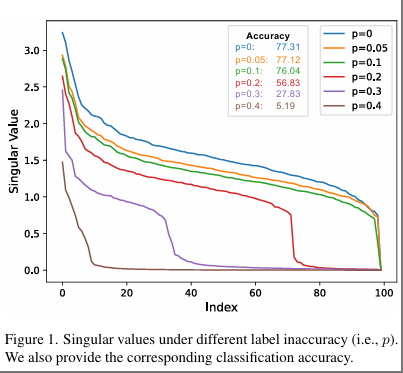
可以观察到权重矩阵的前几个奇异值在标签不准确度的一定范围内没有显著差异。然而，一旦标签不准确度超过某个阈值，前几个奇异值会迅速下降。

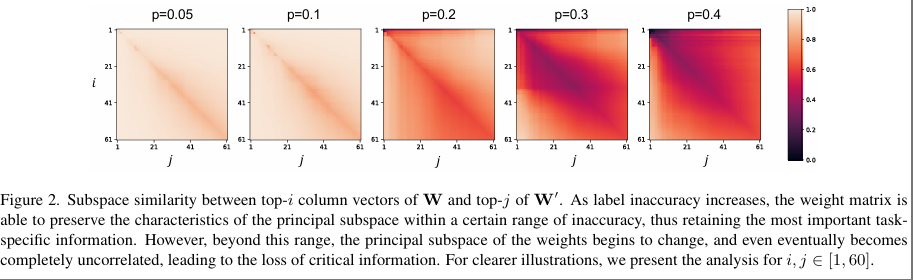
作者又评估了由 V 中前 i 个奇异向量张成的子空间与由 V 中前 j 个奇异向量张成的子空间的相似性。我们基于格拉斯曼距离计算归一化子空间相似度，即
$$
\phi (V,V’,i,j)=\frac{||V _ {:i}^TV _ {:j}^T||_F^2}{min(i,j)}\in[0,1]
$$
随着标签不准确性的增加，V 和 V‘的子空间之间的整体差异变得更加明显。但在一定范围内的标签不准确度，权重的主体子空间基本不受影响，甚至几乎完全相同。

理论

考虑以下分类器（或损失）：
$$
min_W||XW-G||_F^2+\lambda||W||_F^2
$$
闭式解：
$$
W=(X^TX+\lambda I)^{-1}X^TG=K^{-1}X^TG
$$

其实这就是个岭回归线性模型，可能不能代表所有的模型，但是可以作为一个启发。

标签扰动可以表示为$Y=G+M$，其中Y是噪声标签，G是groud truth，M是扰动。
$$
W’=K^{-1}X^TY=K^{-1}X^TG+K^{-1}X^TM=W+\Delta W
$$
而
$$
||\Delta W||_F \le||K^{-1}X^T||_2||M||_F\le||K^{-1}||_2||X^T||_2||M||_F
$$
由于通常情况下 q ≪ n ，X 预期是满秩的。因此有：
$$
\begin{align}
||K^{-1}||_2&=||(X^TX+\lambda I)^{-1}||_2=\frac{1}{\lambda _ {min}(X^TX)+\lambda}
\\
||X^T||_2&=||X||_2=\sigma _ {max}(X)
\end{align}
$$
我们定义标签不准确的程度为 p，即$P(M _ {ij}\ne0)=p$，则$||M||_F=\sqrt{pnl}$，故有
$$
||\Delta W||_F\le \frac{\sigma _ {max}(X)\sqrt{nl}}{\lambda _ {min}(X^TX)+\lambda}\sqrt{p}
$$
根据Davis-Kahan 正弦定理，W 和 W’ 扰动后子空间之间的角度θ的正弦值被限制为$sin\theta\le\frac{||\Delta W||_2}{\delta}$，故$sin\theta\le \frac{\sigma _ {max}(X)\sqrt{nl}}{\delta \lambda _ {min}(X^TX)+\lambda}\sqrt{p}$。

故p比较小的情况下，角度也小。

方法

W 进行奇异值分解，选择前k个。

我们还可以再对剩余的再做一些处理。

假设$U_l=[u _ {k+1},…,u _ {min(q,l)}]$,$V_l=[v _ {k+1},…,v _ {min(q,l)}]$,$\Sigma_l=diag(\sigma _ {k+1},…,\sigma _ {min(q,l)})$，则：
$$
W’=W_k+U_l\Sigma_lV_l^T
$$
为了优化奇异值，我们使用训练数据重新训练它们以提取关键信息，这导致了以下优化问题：
$$
\begin{align}
min _ {\Sigma_l}||XW’-Y||^2_F
\\
s.t. \quad W’=W_k+U_l\Sigma_lV_l^T
\end{align}
$$
上式重写为：
$$
min _ {\Sigma_l}||X(W_k+\sum _ {i=k+1}^{min(q,l)}\sigma_iu_iv_i^T)-Y||^2_F
$$
我们可以直接求导求出来，（所以是免训练的）：
$$
\begin{align}
\sigma_j&=\frac{u_j^TX^T(Y-XW_k)v_j}{u_j^TX^TXu_j}
\\
\Sigma_l^\ast&=\frac{diag(U_l^TX^T(Y-XW_k)V_l)}{diag(U_l^TX^TXU_l)}
\end{align}
$$

题外

图神经网络中也有使用SVD来抵御对抗攻击的。比如WSDM '20的《All You Need Is Low (Rank): Defending Against Adversarial Attacks on Graphs》。

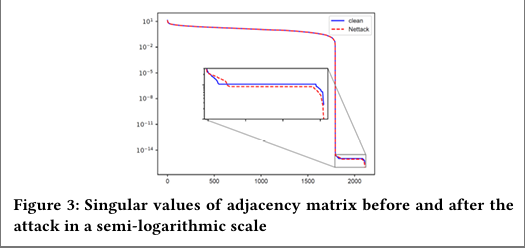
作者发现，Nettack是一种高秩攻击，这是因为Nettack带来的对抗扰动只会影响图中少量的节点，攻击给图结构谱域带来的影响较小，故主要反映在rank较高的奇异值上。

作者同样截断前k个特征值大的作为SVD的近似。但没有对余下的SVD做处理。

作者分析了，说这种近似可能检测不到大于节点度数>$\sigma_r^2-2$的，作者进一步证明了。
$$
Pr(X\ge\sigma_r^2)\approx\frac{\zeta(\alpha,\sigma_r^2)-\zeta(\alpha,d_{max}+1)}{\zeta(\alpha,d_{min})-\zeta(\alpha,d_{max}+1)}<\tau
$$
其中$\zeta(\alpha,x)=\sum_{k=0}^\infty(k+x)^{-\alpha}$，$\alpha\approx 1+|D_G|\left[\sum_{d_i\in D_G} log \frac{d_I}{d_{min-\frac{1}{2}}}\right]$，$D_G=\left\{d_v^G|v\in V,d_v^G\ge d_{min}\right\}$。