18岁的AI天文学家

“18岁美国高中生Matteo Paz利用AI分析NASA的2000亿条数据，发现150万个隐藏天体”（来自公众号）。

该项目与其中一篇论文相关——《A Submillisecond Fourier and Wavelet-based Model to Extract Variable Candidates from the NEOWISE Single-exposure Database》，发表于《The Astronomical Journal》（天文学其中一个重要的期刊）

阅读前介绍

我们先用一句话来概括：

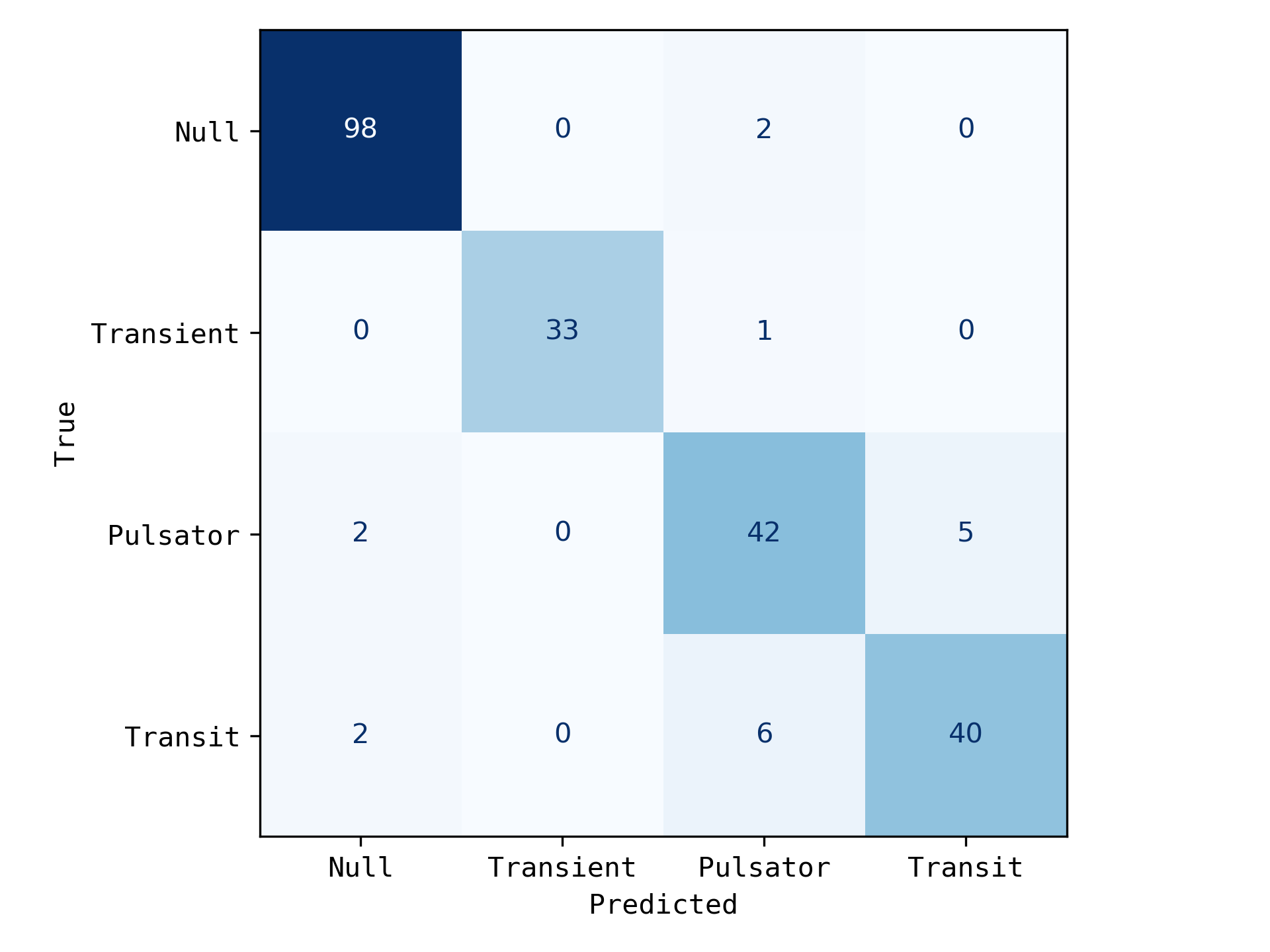
根据光度数据（光变曲线）对星系进行四分类。

研究背景与意义

论文将VARnet应用于近地天体广域红外巡天探测器（NEOWISE）单次曝光数据库，该数据库在10.5年间记录了近2000亿次红外源的出现信息 。研究旨在设计一个流程，从NEOWISE数据中提取可变候选体，以验证VARnet的有效性，并为未来对整个NEOWISE数据集进行变异性调查提供方法论 。

WISE空间望远镜与NEOWISE数据

广域红外巡天探测器（WISE）是一个轨道空间望远镜观测站，最初在2009年至2010年间以四波段红外巡天方式运行 。在固态氢制冷剂耗尽后，它曾短暂作为双波段巡天运行 。经过2011年至2013年12月的休眠期后，该任务以NEOWISE的形式重新启动，持续在其两个最短波长波段收集数据 。由于其长时间尺度和红外灵敏度，WISE为时域天文学研究提供了独特的机会 。

NEOWISE-R单次曝光数据库包含自2013年望远镜重新激活以来每次单次曝光中提取的光度数据 。每次观测（apparition）包含天体的赤经（RA）、赤纬（Dec）、修正儒略日（mjd）以及W1和W2波段的星等数据 。然而，数据库中的数据没有结构，与单个源相关的观测可能分散在数据库中，并且还包含由宇宙射线、条纹曝光或星云造成的噪声观测 。这为收集单个天文物体的数据带来了挑战 。

数据处理

作者将通量变化将恒星分为四种非常广泛的类型：静止型（Nulls）、瞬变型（Transients）、凌星型（Transits）、动型（Pulsating Variables）。

作者也自己声明，这种有限分类法对于变源的全面调查和统计分析并不十分有用。

数据聚类与预处理：

由于望远镜精度的限制和噪声，同一源的中心在每次通过时可能会略有不同，从而形成一个近似二维高斯分布的点云 。研究人员使用基于密度的噪声应用空间聚类（DBSCAN）算法对单次曝光源目录中的观测进行空间聚类，以收集光变曲线数据 。DBSCAN能够稳健地处理不同形状的簇，不需要预先指定簇的数量，并且可以滤除噪声点 。

数据预处理：

为了构建适合神经网络分析的高质量矩阵表示，研究选择了对异常和事件较不敏感的W1波段作为亮度特征 。星等值被转换为绝对通量读数，减去中位数，并使用四分位距进行标准化 。然后使用反正弦双曲函数（arcsinh）将数据压缩到接近[−1,1]的范围 。时间戳（mjd）也被归一化到[0,1]的范围 。测量的预期误差（wlsigmpro）也经过类似的缩放处理并作为模型的特征之一 。最终，每个时间点的数据被表示为一个包含亮度、不确定性和时间戳的三维向量 。

数据生成：

由于已知瞬变源的数量有限，研究人员制定了数学模型来为四种光变类型（静止、瞬变、脉动、凌星）生成模拟的WISE光变曲线，用于训练VARnet 。这些模拟光变曲线的生成考虑了源的基本亮度、噪声水平以及WISE的采样节奏 。

基本函数

在数据生成之前。我们定义一些基本操作。

平均或基础亮度：随机选择一个星等值（范围在6到16等之间，并倾向于选择更暗的星等以模拟天空中的真实分布），然后将其转换为通量值，作为源的基础亮度 ω。

不确定度（噪声标准差）：随机选择一个在 10−4 到 10−1 之间的值作为不确定度 σω，这个值与源的绝对亮度无关，以覆盖各种观测条件（例如，银道面背景光较强导致亮星误差增大，或特定星等下光度测量流程变化导致误差异常） 。

缩放不确定度：NEOWISE数据库中的 wlsigflux 误差值并不直接等于真实亮度值周围的实际离散程度的一个标准差，因此在合成器中使用的不确定度值需要进行缩放以匹配数据库中的值。研究发现，将 $σ_ω$ 乘以一个在0.4到0.6之间随机选择的实数，可以获得最佳性能 。

静止型（Nulls）

简单地选择一个基础通量值，并以该值为均值、特定标准差进行正态分布采样 。

瞬变型（Transients）：

设计了一个基于形态学而非天体物理现象的光度随时间变化的函数模型，能够模拟新星、超新星以及某些类型的瞬变YSO活动等事件 。

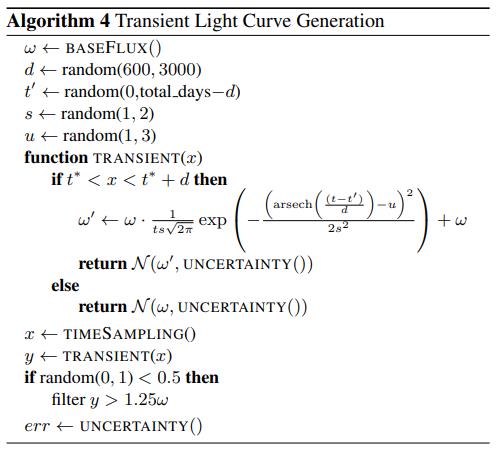
凌星型（Transits）：

采用梯形模型来近似凌星光变曲线，考虑了凌星深度、次凌星深度和周期等因素 。

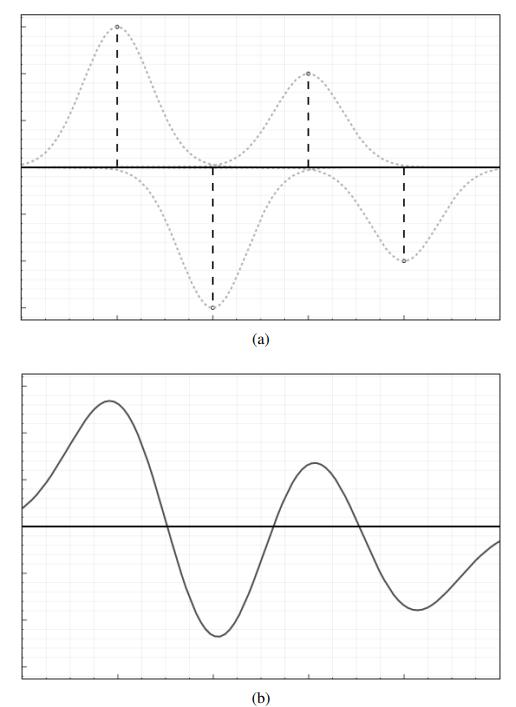
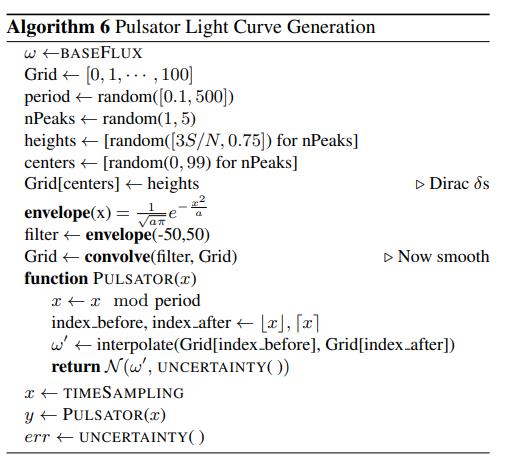
动型（Pulsating Variables）：

通过创建一个表示一个周期的离散网格，在某些点上添加不同高度的狄拉克δ脉冲，然后用高斯滤波器进行离散卷积来生成各种波形 。

模型

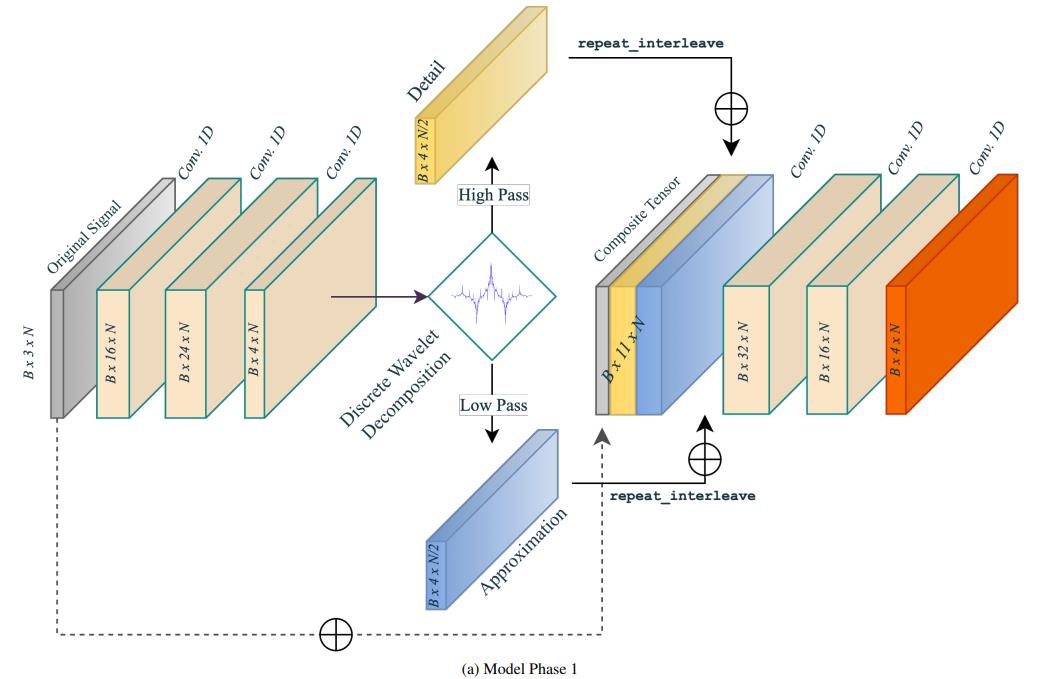
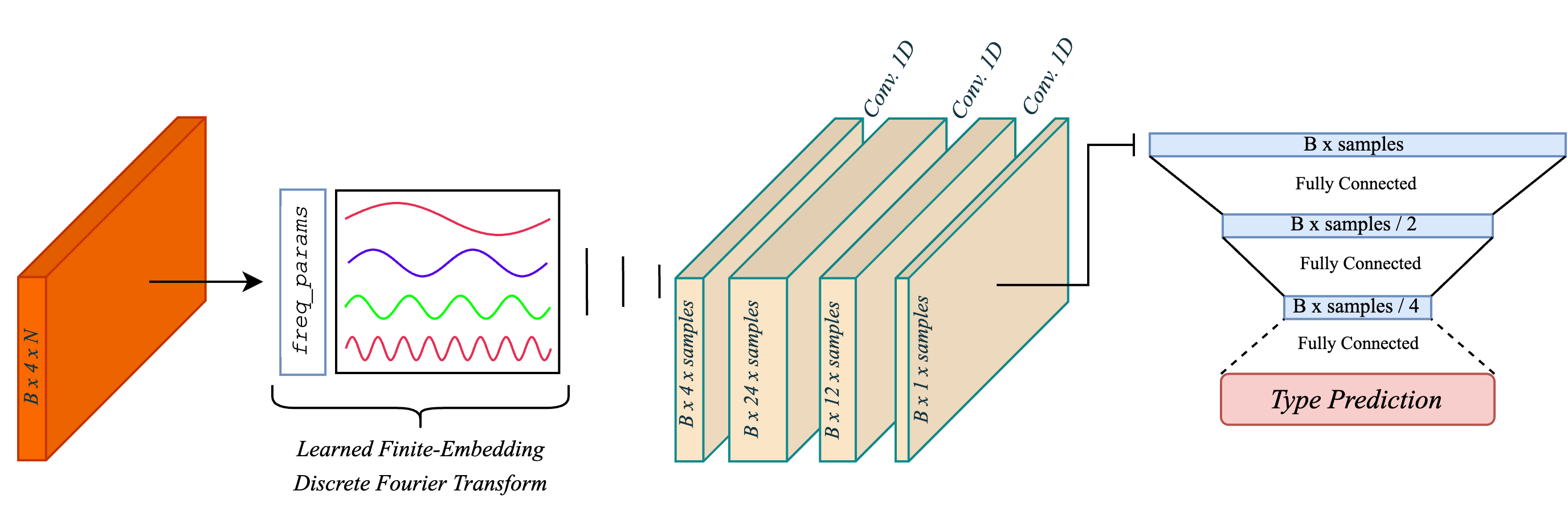
模型除了卷积以外还有小波变换和FFT。

小波变换

这部分没有额外的改进。

即一维离散小波变换就是把信号分别通过低通滤波器和高通滤波器把原始信号分解为原信号的近似系数和原信号的细节系数两个部分，这也被叫做mallat 算法。

FFT

作者觉得DFT时间复杂度太高了，所以进行了优化。
我们称y为a的离散傅里叶变换，其中$w=e^{-i\frac{2\pi}{n}}$：

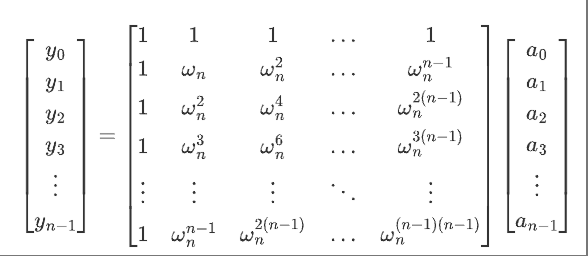
我们取对数，令$z=ln(w)$:

我们可以写成外积的形式$uv^T$:
$$
\begin{align}
u_j=j,0\leq j< N\\
v_j=zj,0\leq j< N
\end{align}
$$
故我们可以给出：
$$
\mathcal{F}(k)=\frac{1}{N}(exp(uv^T)\vec{a})_k
$$
我们可以直接将u作为模型的参数引入，其维度作为超参数。我们将此超参数命名为 samples，并通过以下方式初始化 FEFT：
$$
\begin{align}
a_k\in R^{samples}\\
a_k=\frac{k}{samples}\\
u_k=a_k(N-1)
\end{align}
$$

结果