(几乎涵盖一切的)表示学习统一框架
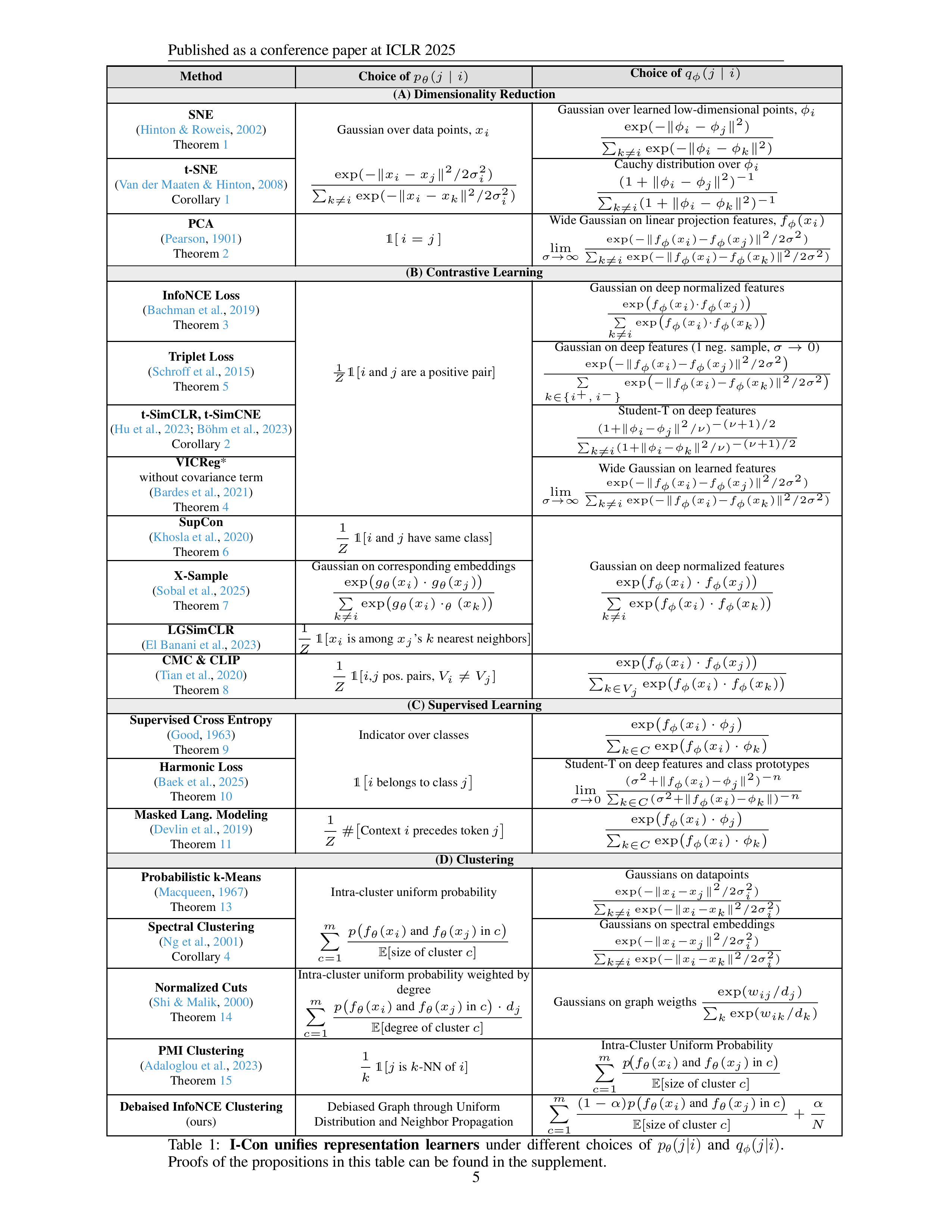
I-Con (I-Con: A Unifying Framework for Representation Learning ,ICLR 2025)是第一个将监督学习、对比学习、聚类和降维目标统一到一个损失函数下的框架,从kmeans、TSNE到SimCLR、CLIP都能统一到一起。

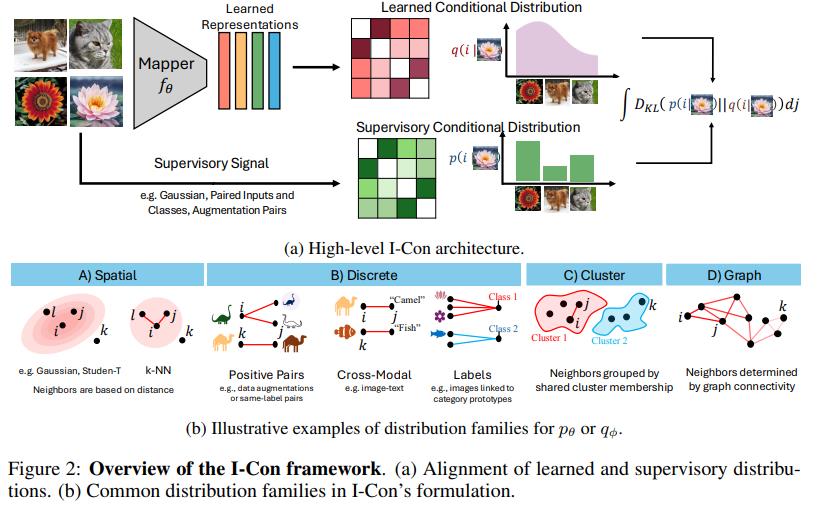
我们首先定义 $x _ {i}\in\mathbb{R}^{d}$ 代表高维数据点, $\phi_{i}\in\mathbb{R}^{m}$ 代表低维嵌,其中 $m\ll d$。
统一SNE
基于SNE的定义,其目标分布(监督部分),由高维空间中的领域分布描述:
$$
p_{\theta}(j|i)=\frac{exp(-||x _ {i}-x _ {j}||^{2}/2\sigma_{i}^{2})}{\sum _ {k\ne i}exp(-||x _ {i}-x _ {k}||^{2}/2\sigma_{i}^{2})}
$$
学习的低维领域分布是:
$$
q_{\phi}(j|i)=\frac{exp(-||\phi_{i}-\phi_{j}||^{2})}{\sum _ {k\ne i}exp(-||\phi_{i}-\phi_{k}||^{2})}
$$
目标是使它们之间的KL散度最小化:
$$
\mathcal{L}=\sum _ {i}D_{KL}(p_{\theta}(\cdot|i)||q_{\phi}(\cdot|i))=\sum _ {i}\sum _ {j}p_{\theta}(j|i)log\frac{p_{\theta}(j|i)}{q_{\phi}(j|i)}
$$
统一tSNE
tSNE和SNE类似,不过低维分布变为了具有一个自由度的student t分布。
$$
q_{\phi}(j|i)=\frac{(1+||\phi_{i}-\phi_{j}||^{2})^{-1}}{\sum _ {k\ne i}(1+||\phi_{i}-\phi_{k}||^{2})^{-1}}
$$
统一PCA
引理1. Let $X:={x _ {i}} _ {i=1}^{n}$, then the following cohesion variance loss
$$
L_{cohesion-var}=\frac{1}{n}\sum _ {ij}w_{ij}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}-2Var(X)
$$
is an instance of I-Con in the special case $w_{ij}=p(j|i)$ and $q_{\phi}$ is Gaussian as with a large width as $\sigma\rightarrow\infty$
证明:By using AM-GM inequality, we have [cite: 269]
$\frac{1}{n}\sum _ {k=1}^{n}e^{-z_{k}}\ge(\Pi_{k=1}^{n}e^{-z_{k}})^{\frac{1}{n}}\Rightarrow\frac{1}{n}\sum _ {k=1}^{n}e^{-z_{k}}\ge(e^{-\sum _ {k=1}^{n}z_{k}})^{\frac{1}{n}}$
which implies that
$log\sum _ {k=1}^{n}e^{-z_{k}}-logn\ge log(e^{-\sum _ {k=1}^{n}z_{k}})^{\frac{1}{n}}\Rightarrow log\sum _ {k=1}^{n}e^{-z_{k}}\ge-\frac{1}{n}\sum _ {k=1}^{n}z_{k}+log(n)$
Alternatively, this can be written as
$-log\sum _ {k=1}^{n}e^{-z_{k}}\le\frac{1}{n}\sum _ {k=1}^{n}z_{k}-log(n)$
Now assume that we have a Gaussian Kernel $q_{\phi}$ [cite: 269]
$q_{\phi}(j|i)=\frac{exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}/\sigma^{2})}{\sum _ {k\ne i}exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2}/\sigma^{2})}$
Therefore, given the inequality of exp-sum that we showed above, we have [cite: 269]
$logq_{\phi}(j|i)=-\frac{||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}}{\sigma^{2}}-log\sum _ {k\ne i}exp(-\frac{||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2}}{\sigma^{2}})$
$\le-\frac{1}{\sigma^{2}}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}+\frac{1}{n\sigma^{2}}\sum _ {k\ne i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2}-log(n)$
$=-\frac{1}{\sigma^{2}}(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}+\frac{1}{n}\sum _ {k\ne i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2})-log(n)$Therefore, the cross entropy $H(p_{\theta},q_{\phi})$ is bounded by [cite: 269]
$H(p_{\theta},q_{\phi})=-\frac{1}{n}\sum _ {i}\sum _ {j}p(j|i)logq_{\phi}(j|i)$
$\le\frac{1}{n}\sum _ {i}\sum _ {j}p(j|i)(\frac{1}{\sigma^{2}}(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}+\frac{1}{n}\sum _ {k\ne i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2})-log(n))$
$=\frac{1}{\sigma^{2}}(\frac{1}{n}\sum _ {ij}p(j|i)||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}-\frac{1}{n^{2}}\sum _ {ijk}p(j|i)||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2})-log(n)$
$=\frac{1}{\sigma^{2}}(\frac{1}{n}\sum _ {ij}p(j|i)||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}-2Var(X))+log(n)$
$=\frac{1}{\sigma^{2}}(\frac{1}{n}\sum _ {ij}p(j|i)||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}-2Var(X))+log(n)$
$=\frac{1}{\sigma^{2}}\mathcal{L} _ {cohesion-var}+log(n)$On the other hand, the L.H.S. can be upper bounded by using second order bound $e^{-z}\le1-z+z^{2}/2$, which implies that [cite: 270]
$-log\sum _ {k=1}^{n}e^{-z_{k}}\ge log(1-\frac{1}{n}\sum _ {k=1}^{n}z_{k}+\frac{1}{n}\sum _ {k=1}^{n}z_{k}^{2})-log(n)$ [cite: 270]
— PAGE 19 —
On the other hand, $log(1+u)\ge u-u^{2}/2$, therefore, [cite: 271]
$-log\sum _ {k=1}^{n}e^{-z_{k}}\ge(1-\frac{1}{n}\sum _ {k=1}^{n}z_{k}+\frac{1}{n}\sum _ {k=1}^{n}z_{k}^{2})-\frac{1}{2}(1-\frac{1}{n}\sum _ {k=1}^{n}z_{k}+\frac{1}{n}\sum _ {k=1}^{n}z_{k}^{2})^{2}-log(n)$
Therefore, in the limit $\sigma\rightarrow\infty$ the bounds become tighter and the I-Con loss approaches the cohesion variance loss. [cite: 271] $\Pi$ [cite: 272]
根据引理1, 当 $p_{j|i}=1[i=j]$ 我们有
$$
\begin{align}
\mathcal{L}&=\frac{1}{n}\sum _ {ij}p_{j|i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}-2Var(X)
\\
&=\frac{1}{n}\sum _ {i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {i})||^{2}-2Var(X)
\\
&=-2Var(X)
\end{align}
$$
故最小化 L 等于最大化方差,这与PCA的目标一致。如果我们限制 $f _ {\phi}$为一个线性投影映射,则等同于PCA。
统一InfoNCE
InfoNCE 旨在最大化正样本对之间的相似度,同时最小化负样本对之间的相似度,在学习的特征空间中。在 I-Con 框架中,这可以解释为最小化两个分布之间的散度:原始空间中的邻域分布和学习到的嵌入空间中的分布。
$$
p_{\theta}(j|i)=\begin{cases}\frac{1}{k},x_j为x_i的k \ positive \ views\\ 0\end{cases}
$$
其中 k 是$x _ {i}$ 的positive pairs数量。
$q_{\phi}(j|i)$ 基于 $f _ {\phi}(x _ {i})$ 和 $f _ {\phi}(x _ {j})$之间相似度,并约束在单位范数上 $(||f _ {\phi}(x _ {i})||=1)$ 。使用一个带温度系数的高斯核为:
$$
q_{\phi}(j|i)=\frac{exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {j})/\tau)}{\sum _ {k\ne i}exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {k})/\tau)}
$$
$||f _ {\phi}(x _ {i})||=1$, $f _ {\phi}(x _ {i})$ 和 $f _ {\phi}(x _ {j})$ 之间的欧氏距离为 $2-2(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {j}))$
而
$$
\mathcal{L} _ {InfoNCE}=-\sum _ {i}log\frac{exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {i}^{+})/\tau)}{\sum _ {k}exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {k})/\tau)}
$$
故
$$
\mathcal{L} _ {InfoNCE}\propto\sum _ {i}\sum _ {j}p_{\theta}(j|i)logq_{\phi}(j|i)=H(p_{\theta},q_{\phi})
$$
H表示交叉熵,因为 $p_{\theta}(j|i)$ 是固定的,所以最小化交叉熵等价于最小化KL散度。
统一VICReg
根据引理 1,我们知道任何凝聚方差形式的损失都是I-Con 的一个实例。
$$
\mathcal{L}=\frac{1}{n}\sum _ {ij}p_{j|i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}-2Var(X)
$$
若我们选择 $p_{j|i}$ 作为正样本对的指示器, i and $i^{+}$, 则:
$$
\mathcal{L}=\frac{1}{n}\sum _ {i}||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {i^{+}})||^{2}-2Var(X)
$$
这是没有协方差项且不变性-方差项比例为 1:2 的 VICReg 损失。观察到 VICReg 没有负样本,因为它对所有点施加相等的排斥力。这相当于在嵌入上的条件高斯分布中取 $\sigma\rightarrow\infty$ 。
统一Triplet Loss
$$
P_{\theta}(j|i) = \begin{cases} 1 & \text{if } x _ {j} \text{ is among the k positive views of } x _ {i}
\\
0 & \text{otherwise,} \end{cases}
$$
$$
q_{\phi}(j|i)=\frac{exp(-\frac{||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2}}{\sigma^{2}})}{\sum _ {k\ne i}exp(-\frac{||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2}}{\sigma^{2}})^{2}}
$$
特别仅考虑两个邻居的特殊情况下,一个是正视图,一个是负视图。
为了简化,我们设置 $\sigma=1$ 。
$$
\mathcal{L}=-\frac{1}{N}\sum _ {i}\sum _ {j}q_{\phi}(j|i)log\frac{exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2})}{\sum _ {k\ne i}exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2})}
$$
在锚点 $x _ {i}$ 恰好有一个正例 $x _ {i}^{+}$ 和一个负例 $x _ {i}^{-}$ 的情况下,分母简化为:
$$
\sum _ {k\ne i}exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2})=exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {i}^{+})||^{2})+exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {i}^{-})||^{2})
$$
将 $d_{i}^{+}=||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {i}^{+})||^{2}$ 和 $d_{i}^{-}=||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {i}^{-})||^{2}$代入损失函数,我们得到:
$$
\begin{align}
\mathcal{L}&=-\frac{1}{N}\sum _ {i}log\frac{exp(-d_{i}^{+})}{exp(-d_{i}^{+})+exp(-d_{i}^{-})}
\\
&=-\frac{1}{N}\sum _ {i}log(\frac{1}{1+exp(d_{i}^{-}-d_{i}^{+})})
\\
&=\frac{1}{N}\sum _ {i}log(1+exp(d_{i}^{+}-d_{i}^{-}))
\end{align}
$$
我们知道:
$$
max(z,0)\le log(1+exp(z))\le max(z,0)+log(2)
$$
则有:
$$
\frac{1}{N}\sum _ {i}max(d_{i}^{+}-d_{i}^{-},0)\le\mathcal{L}\le\frac{1}{N}\sum _ {i}max(d_{i}^{+}-d_{i}^{-},0)+log(2)
$$
左侧是 Triplet loss $\mathcal{L} _ {Triplet}=\frac{1}{N}\sum _ {i}max(d_{i}^{+}-d_{i}^{-},0)$,故有以下bounds:
$$
\mathcal{L}-log(2)\le\mathcal{L} _ {Triplet}\le\mathcal{L}
$$
对于一般的 $\sigma$, 不等式界限为:
$$
\mathcal{L} _ {\sigma}-\sigma^{2}log(2)\le\mathcal{L} _ {Triplet}\le\mathcal{L} _ {\sigma}
$$
其中
$$
\mathcal{L} _ {\sigma}=-\frac{\sigma^{2}}{N}\sum _ {i}\sum _ {j}q_{\phi}(j|i)log\frac{exp(-\frac{||f _ {\sigma}(x _ {i})-f _ {\phi}(x _ {j})||^{2}}{\sigma^{2}})}{\sum _ {k\ne i}exp(-\frac{||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2}}{\sigma^{2}})}
$$
当 $\sigma\to 0$, $\mathcal{L} _ {Triplet}$ 接近于 $\mathcal{L} _ {\sigma}$
统一有监督对比损失
从统一InfoNCE的式子来看,定义:
$$
q_{\phi}(j|i)=\frac{exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {j})/\tau)}{\sum _ {k\ne i}exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {k})/\tau)}
$$
$$
p_{\theta}(j|i)=\frac{1}{K_{i}-1}1[i \text{ and } j \text{ share the same label}]
$$
其中 $f _ {\phi}$ 是映射到 deep feature space 的, $K_{i}$ 是类i样本数。
统一X-Sample对比损失
考虑以下p在相应特征(例如图像的caption embeddings)上的分布
$$
\frac{exp(g _ {\theta}(x _ {i})\cdot g _ {\theta}(x _ {j}))}{\sum _ {k\ne i}exp(g _ {\theta}(x _ {i})\cdot_{\theta}(x _ {k}))}
$$
和大多数特征学习方法类似,学习到的分布是关于学习嵌入的余弦距离的高斯分布
$$
q_{\phi}(j|i)=\frac{exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {j}))}{\sum _ {k\ne i}exp(f _ {\phi}(x _ {i})\cdot f _ {\phi}(x _ {k}))}
$$
统一CMC和CLIP
CMC(Contrastive Multiview Coding) 和 CLIP 的关键区别在于它们优化了跨不同模态的alignment, $p_{\theta}(j|i)$ 可以表示为
$$
p_{\theta}(j|i)=\frac{1}{Z}1[i \text{ and } j \text{ are positive pairs and } V_{i}\ne V_{j}]
$$
其中 $V_{i}$ and $V_{j}$ 表示 $x _ {i}$ and $x _ {j}$的模态集。在这里 $p_{\theta}(j|i)$ 对从不同模态中抽取的正样本对赋予均匀概率。这个学习到的分布 $q_{\phi}(j|i)$是基于深度特征之间的高斯相似度,但条件是来自相反模态集的点。因此,学习到的分布定义为:
$$
q_{\phi}(j|i)=\frac{exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {j})||^{2})}{\sum _ {k\in V_{j}}exp(-||f _ {\phi}(x _ {i})-f _ {\phi}(x _ {k})||^{2})}
$$
统一交叉熵
交叉熵可以看作是CMC的特例,其中一个视角对应数据点特征,另一个对应类别logit。
统一Harmonic Loss
这相当于从交叉熵中的 $q(j|i)$ 高斯分布移动到student-t分布,类似于从 SNE 移动到 t-SNE。更具体地说,令V 为数据点集,C为类原型集, $\phi_{i}$ 为第 i 类的学习到的类原型, n为谐波损失度。
考虑以下p这是一个数据标签指示器( data-label indicator)。
$$
p(j|i)=1[i \text{ belongs to class } j]
$$
和以下q,这是一个2n-1自由度的student-t分布:
$$
lim_{\sigma\rightarrow0}\frac{(1+||f _ {\phi}(x _ {i})-\phi_{j}||^{2}/((2n-1)\sigma^{2}))^{-n}}{\sum _ {k\in C}(1+||f _ {\phi}(x _ {i})-\phi_{k}||^{2}/((2n-1)\sigma^{2}))^{-n}}
$$
它可以写成:
$$
lim_{\sigma\rightarrow0}\frac{(((2n-1)\sigma^{2})+||f _ {\phi}(x _ {i})-\phi_{j}||^{2})^{-n}}{\sum _ {k\in C}((2n-1)\sigma^{2})+||f _ {\phi}(x _ {i})-\phi_{k}||^{2}/)^{-n}}
$$
当 $\sigma\rightarrow\infty$ 损失函数为$\mathcal{L}=\sum _ {i\in C}\frac{(||f _ {\phi}(x _ {i})-\phi_{j}||^{2})^{-n}}{\sum _ {k\in C}(||f _ {\phi}(x _ {i})-\phi_{k}||^{2}/)^{-n}}$
统一MLM
在掩码语言建模(MLM)中,目标是为被掩码的词j预测其周围的上下文$x_i$。这种设置自然地符合 I-Con 框架。
目标分布 $p_{\theta}(j|i)$ 是关于上下文i和tokens j的经验分布,定义为:
$$
p_{\theta}(j|i)=\frac{1}{Z}\#[\text{Context } i \text{ precedes token } j]
$$
其中 $\#[\text{Context } i \text{ precedes token } j]$ 表示在训练语料库中tokensj与上下文x_i之后出现的次数, Z是一个归一化常数,以确保 $\sum _ {j}p_{\theta}(j|i)=1$。
$q_{\phi}(j|i)$ 使用神经网络输出的tokens预测logits进行建模,它被定义为上下文嵌入 $f _ {\phi}(x _ {i})$ 和 token 嵌入 $\phi_{j}$ 的点积的softmax:
$$
q_{\phi}(j|i)=\frac{exp(f _ {\phi}(x _ {i})\cdot\phi_{j})}{\sum _ {k\in\mathcal{V}}exp(f _ {\phi}(x _ {i})\cdot\phi_{k})}
$$
其中 $f _ {\phi}(x _ {i})$ 是模型生成的上下文 $x _ {i}$ 的嵌入, $\phi_{j}$ 是token j的嵌入,V是所有可能tokens的词汇表。
MLM 损失旨在最小化目标分布p和学习分布q之间的交叉熵:
$$
\mathcal{L} _ {MLM}=-\sum _ {i}\sum _ {j}p_{\theta}(j|i)logq_{\phi}(j|i)=H(p_{\theta},q_{\phi})
$$
由于在实践中,对于每个 $x _ {i}$ 仅考虑真实的masked token $j_{i}^{*}$ ,目标分布简化为:
$$
p_{\theta}(j|i)=\delta_{j,j_{i}^{*}}
$$
其中 $\delta_{j.j_{i}^{}}$ 是 Kronecker delta function, 当 $j=j_{i}^{}$ 时等于1,否则为0
代入损失函数,MLM损失变为:
$$
\mathcal{L} _ {MLM}=-\sum _ {i}logq_{\phi}(j_{i}^{*}|x _ {i})
$$
统一Kmeans
经典Kmeans的定义:
$$
\mathcal{L} _ {k-Means}=\sum _ {i=1}^{N}\sum _ {c=1}^{m}1(c^{(i)}=c)||x _ {i}-\mu_{c}||^{2}
$$
$c^{(i)}$代表聚类分配:
$$
c^{(i)}=argmin_{c}||x _ {i}-\mu_{c}||^{2}
$$
Probabilistic K-means 松弛
在probabilistic K-means, $x _ {i}$ 属于c类的概率为 $\phi_{ic}$。
$$
\mathcal{L} _ {Prob-k-Means}=\sum _ {i=1}^{N}\sum _ {c=1}^{m}\phi_{ic}||x _ {i}-\mu_{c}||^{2}
$$
为了能融入到我们的框架中,我们尽量把它融入到对比学习那一套中。
似然 K-means 的对比公式
定义条件概率为 $q_{\phi}(j|i)$ :
$$
q_{\phi}(j|i)=\sum _ {c=1}^{m}\frac{\phi_{ic}\phi_{jc}}{\sum _ {k=1}^{N}\phi_{kc}}
$$
我们可以将probabilistic K-means 重新表述为对比损失:
$$
\mathcal{L}=-\sum _ {i,j}(x _ {i}\cdot x _ {j})q_{\phi}(j|i)
$$
证明:
$$
\mathcal{L} _ {Prob-k-Means}=\sum _ {i=1}^{N}\sum _ {c=1}^{m}\phi_{ic}||x _ {i}-\mu_{c}||^{2}
$$
展开:
$$
\mathcal{L} _ {Prob\cdot k\cdot Means}=\sum _ {c=1}^{m}(\sum _ {i=1}^{N}\phi_{ic})||\mu_{c}||^{2}-2\sum _ {c=1}^{m}(\sum _ {i=1}^{N}\phi_{ic}x _ {i})\cdot\mu_{c}+\sum _ {i=1}^{N}||x _ {i}||^{2}
$$
使该损失最小化的聚类中心由下式给出:
$$
\mu_{c}=\frac{\sum _ {i=1}^{N}\phi_{ic}x _ {i}}{\sum _ {i=1}^{N}\phi_{ic}}
$$
代回损失函数的式子,得到:
$$
\mathcal{L}=-\sum _ {i,j}(x _ {i}\cdot x _ {j})q_{\phi}(j|i)
$$
备选损失函数:
$$
\mathcal{L}=-\sum _ {i,j}||x _ {i}-x _ {j}||^{2}q_{\phi}(j|i)
$$
在${\phi_{ic}}$的最小化下,它会产生相同的最佳聚类分配。
证明:在损失函数中展开平方范数得到:
$$
\begin{align}
\mathcal{L}&=-\sum _ {i,j}(||x _ {i}||^{2}-2x _ {i}\cdot x _ {j}+||x _ {j}||^{2})q_{\phi}(j|i)$
\\
&=2(-\sum _ {i,j}x _ {i}\cdot x _ {j}q_{\phi}(j|i))
\end{align}
$$
PROBABILISTIC K-MEANS 作为 I-Con 方法
令 $q_{\phi}(j|i)$ 表示从$x _ {i}$的聚类中随机选择 $x _ {j}$ 的概率:
$$
q_{\phi}(j|i)=\sum _ {c=1}^{m}\frac{\phi_{ic}\phi_{jc}}{\sum _ {k=1}^{N}\phi_{kc}}
$$
定义:
$$
p_{\theta}(j|i)=\frac{exp(-||x _ {i}-x _ {j}||^{2}/2\sigma^{2})}{\sum _ {k}exp(-||x _ {i}-x _ {k}||^{2}/2\sigma^{2})}
$$
$$
q_{\phi}(j|i)=\sum _ {c=1}^{m}\frac{\phi_{ic}\phi_{jc}}{\sum _ {k=1}^{N}\phi_{kc}}
$$
则
$$
\mathcal{L} _ {c\cdot SNE}=\sum _ {i}D_{KL}(q_{\phi}(\cdot|i)||p_{\theta}(\cdot|i))
$$
$$
\mathcal{L} _ {c\cdot SNE}=\frac{1}{2\sigma^{2}}\mathcal{L} _ {Pmb\cdot k\cdot Means}-\sum _ {i}H(q_{\phi}(\cdot|i))
$$
证明:假设 $2\sigma^{2}=1$。记 $\sum _ {k}exp(-||x _ {i}-x _ {k}||^{2})$ 为 $Z_{i}$,则有:
$$
logp_{\theta}(j|i)=-||x _ {i}-x _ {j}||^{2}-logZ_{i}
$$
令 $\mathcal{L} _ {i}$ 为 $-\sum _ {j}||x _ {i}-x _ {j}||^{2}q_{\phi}(j|i)$ ,则:
$$
\begin{align}
\mathcal{L} _ {i}&=-\sum _ {j}||x _ {i}-x _ {j}||^{2}q_{\phi}(j|i)
\\&=\sum _ {j}(log(p_{\theta}(j|i))+log(Z_{i}))q_{\phi}(j|i)
\\&=\sum _ {j}q_{\phi}(j|i)log(p_{\theta}(j|i))+\sum _ {j}q_{\phi}(j|i)log(Z_{i})
\\&=\sum _ {j}q_{\phi}(j|i)log(p_{\theta}(j|i))+log(Z_{i})
\\&=H(q_{\phi}(\cdot|i),p_{\theta}(\cdot|i))+log(Z_{i})
\\&=D_{KL}(q_{\phi}(\cdot|i)||p_{\theta}(\cdot|i))+H(q_{\phi}(\cdot|i))+log(Z_{i})
\end{align}
$$
故:
$$
\begin{align}
\mathcal{L} _ {Prob-KMeans}&=-\sum _ {i}\sum _ {j}||x _ {i}-x _ {j}||^{2}q_{\phi}(j|i)=\sum _ {i}\mathcal{L} _ {i}
\\&=\sum _ {i}D_{KL}(q_{\phi}(\cdot|i)||p_{\theta}(\cdot|i))+H(q_{\phi}(\cdot|i))+log(Z_{i})
\\&=\mathcal{L} _ {c.SNE}+\sum _ {i}H(q_{\phi}(\cdot|i))+constant
\end{align}
$$
因此,
$$
\mathcal{L} _ {c\cdot SNE}=\mathcal{L} _ {Prob-KMeans}-\sum _ {i}H(q_{\phi}(\cdot|i))
$$
如果我们允许 $\sigma$ 为任何值:
$$
\mathcal{L} _ {c\cdot SNE}=\frac{1}{2\sigma^{2}}\mathcal{L} _ {Prob\cdot KMeans}-\sum _ {i}H(q_{\phi}(\cdot|i))
$$
注意上述关系仅差一个加性常数。这意味着最小化具有熵正则化的对比概率 K-means 损失,等价于最小化KL 散度之和。
统一谱聚类
谱聚类通过首先使用归一化拉普拉斯矩阵的前 k 个特征向量将数据嵌入到低维空间中,扩展了这个想法。亲和矩阵 A是通过相似性度量(例如径向基函数核)构建的,并编码了数据点之间的分配概率。在这个转换下,谱聚类是投影嵌入上的 I-Con 的一个实例。
统一Normalized Cuts
其损失函数定义为:
$$
\mathcal{L} _ {NomCus}=\sum _ {c=1}^{m}\frac{cut(A_{c},\overline{A} _ {c})}{vol(A_{c})}
$$
其中 $A_{c}$ 为对应于聚类c的数据子集, $\overline{A} _ {c}$ 是其补集, $cut(A_{c},\overline{A_{c}})$ 表示 $A_{c}$ 和 $\overline{A} _ {c}$之间的边权重之和,而 $vol(A_{c})$ 是聚类 $A_{c}$ 的总体积/边权重之和。
类似于 K-Means,通过以软分配的对比方式重新表述这一点,学习到的分布可以表示为概率簇分配 $\phi_{ic}=p(c|x _ {i})$ :
$$
q_{\phi}(j|i)=\sum _ {c=1}^{m}\frac{\phi_{ic}\phi_{jc}d_{j}}{\sum _ {k=1}^{N}\phi_{kc}d_{k}}
$$
其中d为节点的度数。
统一互信息聚类
鉴于 SimCLR、K-Means 和 I-Con 框架之间已建立的联系,这一结果自然而然地得出。具体来说,目标分布 $p_{\theta}(j|i)$ 是观测到的正对的一个均匀分布:
$$
P_{\theta}(j|i) = \begin{cases} 1 & \text{if } x _ {j} \text{ is among the k positive views of } x _ {i} \\ 0 & \text{otherwise.} \end{cases}
$$
另一方面,学习到的嵌入 $\phi_{i}$ 表示 $x _ {i}$ 被分配到聚类中的概率。因此,类似于 K-Means 连接的分析,学习到的分布被建模为:
$$
q_{\phi}(j|i)=\sum _ {c=1}^{m}\frac{\phi_{ic}\phi_{jc}}{\sum _ {k=1}^{N}\phi_{kc}}
$$
统一变分法
互信息的变分界限被广泛探索,并与 InfoNCE 等损失函数联系起来,其中最小化 InfoNCE 最大化互信息下界(Oord 等人,2018;Poole 等人,2019)。证明通常从重写互信息开始:
$$
I(X;Y)=\mathbb{E} _ {p(x,y)}[log\frac{q(x|y)}{p(x)}]+\mathbb{E} _ {p(y)}[D_{KL}(p(x|y)||q(x|y))]
$$
我们一般假设 $p(x _ {i})=\frac{1}{N}$ ,则 $p(x,y)=\frac{1}{N}p(x|y)$。互信息下界变为
$$
\begin{align}
I(X;Y)&\geq \mathbb{E} _ {p(x,y)}[logq(x|y)]-\mathbb{E} _ {p(x,y)}[log p(x)]
\\&=\mathbb{E} _ {p(x,y)}[logq(x|y)]+log(N)
\\&=\frac{1}{N}\sum _ {x,y\in\mathcal{X}\times\mathcal{X}}p(x|y)logq(x|y)+log(N)
\\&=\frac{1}{N}\sum _ {y\in\mathcal{X}}\sum _ {x\in\mathcal{X}}p(x|y)logq(x|y)+log(N)
\\&=-H(p(x|y),q(x|y))+log(N)
\end{align}
$$
因此,最大化两个分布之间的交叉熵会最大化样本之间的互信息。
变分贝叶斯中的近似是通过最小化变分分布和真实后验之间的 KL散度来实现的:
$$
KL(q_{\phi}(z)||p(z|x))=\mathbb{E} _ {q_{\phi}(z)}[log\frac{q_{\phi}(z)}{p(z|x)}]
$$
优化目标(被称为ELBO):
$$
ELBO=\mathbb{E} _ {q_{\varphi}(z)}[logp(x,z)]-\mathbb{E} _ {q_{\varphi}(z)}[logq_{\phi}(z)]
$$
最大化 ELBO 等价于最小化 KL 散度,从而确保 $q_{\phi}(z)$ 接近 $p(z|x)$。VB 可以通过在变量和分布之间进行特定映射,在 I-Con 框架内进行描述。让i对应数据点x,j对应潜变量z,我们可以将监督分布 $p_{\theta}(z|x)$ 设置为真实后验$p(z|x)$。我们可以定义学习到的分布 $q_{\phi}(z|x)$ 与x无关,即 $q_{\phi}(z|x)=q_{\phi}(z)$。
则I-Con loss 简化为:
$$
\mathcal{L}(\phi)=\int_{x\in\mathcal{X}}KL(p(z|x)||q_{\phi}(z))dx=\mathbb{E} _ {p(x)}[KL(p(z|x)||q_{\phi}(z))]
$$