同质性对图神经网络是必需的吗?
出自《Is homophily a necessity for graph neural networks? 》ICLR, 2022.
GNNs 通常被认为由于同质性假设(“物以类聚”)而工作良好,但在异质性图中(不同节点相连)泛化能力较差。
这篇论文则认为,如果图中的同一类的结点具有相似的邻居的分布, 则 Homophily 不是必须的。
同质性假设
同质性可以分为:
标签同质性:即同一类别的节点更易相连
特征同质性:具有相似特征向量的节点,比特征差异很大的节点,更有可能通过一条边相连。
业界一致认为同质性是GNN的必要前提。
比如像《A Unified View on Graph Neural Networks as Graph Signal Denoising》(CIKM), 2021.。甚至认为这些GNN(GCN、GAT、PPAP等)其实都是以下问题的形式:
$$
argmin_F L=||F-S||_F^2+c*tr(F^TLF)
$$
我们在这里只讲一下GCN。
$$
\nabla L=2||F-S||+2cLF
\mathop{=}^{F=S}2cLS
$$
如果我们采用梯度下降求解:
$$
\begin{align}
F&=S-\lambda (2cLS)=(1-2\lambda c)S+2\lambda cAS
\\
&\mathop{=}^{\lambda=1/2c,S=X’}AX’
\end{align}
$$
即GCN的aggregation。
我们真的需要同质性吗
论文首先举了个这个例子,可以发现这个图中所有蓝色节点将具有1的表示,而橙色节点将具有0的表示。
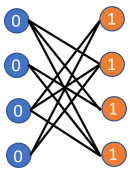
如果图中的同一类的结点具有相似的邻居的分布, 则 Homophily 不是必须的,比如:
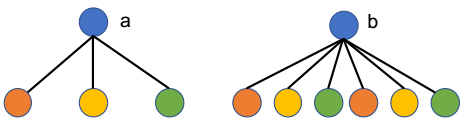
严谨地,论文同样从contextual stochastic block model(CSBM)入手,证明了
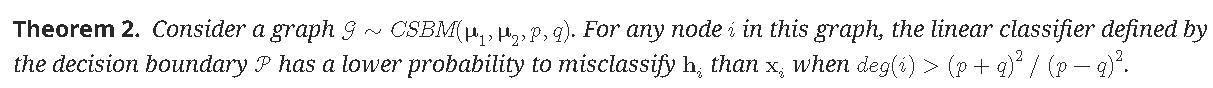
$CBSM(\mu_1,\mu_2,p,q)$表示两个社区,若节点i和j属于同一社区,则它们之间有边的概率为$P(A_{ij}=1)=p$,若节点i和j属于不同社区,则它们之间有边的概率为$P(A_{ij}=1)=q$,
同质性为$\frac{p}{p+q}$。
这句话的意思是,比如在极端情况下,p=9q或q=9p,则$(p+q)^2/(p-q)^2=1.23$,只要节点度数大于1(这个条件很容易达到),是可以被区分的,故没有同质性并不会影响GCN的性能。