Fourier Position Embedding

Fourier Position Embedding（FOPE)出自ICML2025，对当前LLM常用的ROPE进行了改进，认为ROPE默认“每一维只存在单一频率的语义”是过于理想的，所以提出了增加更多的频率（比如基于傅里叶）的方法。

旋转位置编码

旋转式位置编码（Rotary Position Embedding，RoPE）由苏神提出，在其博客中也有介绍。

我们也可以重温一下。

我们想要一个又有绝对位置，又有相对位置的编码。苏神假定存在恒等关系：
$$
<f(q,m),f(k,n)>=g(q,k,m-n)
$$
苏神找到了以下f：$f(q,m)=qe^{im\theta}$。

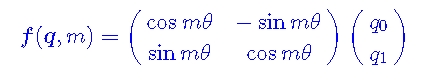
我们可以把它扩展到更多维：

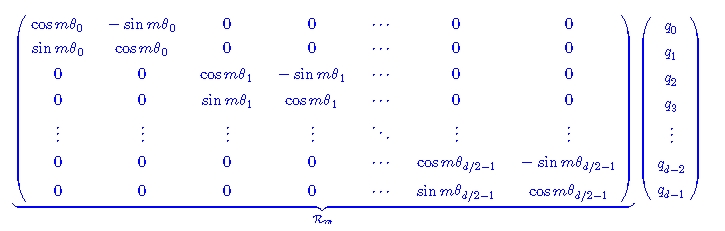
注意到[[A,O][O,B]]*[[C,O][O,D]]=[[AC,O][O,BD]]

所以这样拼接，原本的性质是不会被破坏的。

动机

ROPE看上去已经很不错了，但是它会有什么问题呢？

线性层会混杂频率：

线性层WX由于是对所有元素进行操作，自然而然会产生混杂。

激活函数会混杂频率：

作者以非线性函数和泰勒展开的角度，假设非线性函数可以展开为$\sum ax^n$，这样会有交互项。比如$(sin\theta+cos\theta)^2=1+sin2\theta$，这会引入一个新频率。

我感觉这里怪怪的

时域截断：

即由于时域截断，也会产生新的频率。

即正常的应为只在0处有值，但经过时域截断后，会变为：

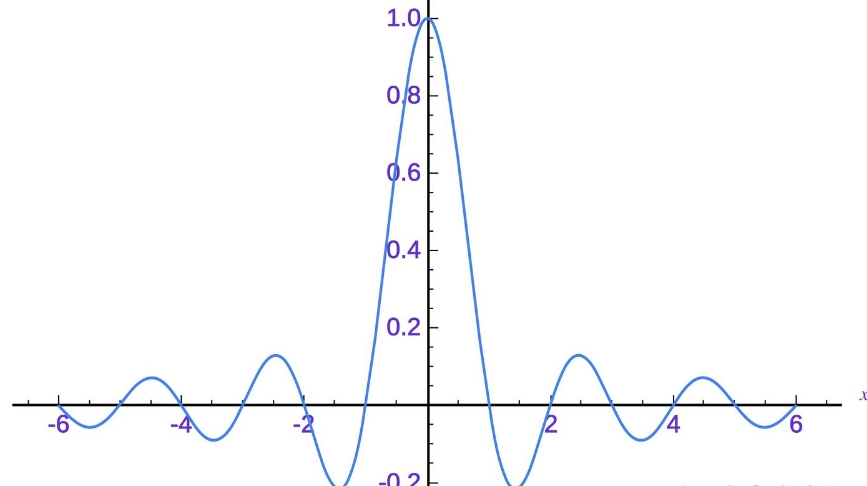
其他地方也会有频率掺杂进来了。

（比较经典的信号与系统知识。）

怎么做

① 既然每一维中不可避免的混杂其他频率的分量，那就干脆在一开始就把每一维都建模成一个傅里叶级数（Fourier Series）。即使这样的建模不会避免频谱破坏，FoPE却可以在每一维中分解出更多频率的信息（利用三角函数的正交性），从而让更多的频率分量保持周期延拓性；

② 既然极低频的分量周期过长，会导致这些频率分量的周期特性无法被学习到，那就将他们裁剪成频率为0的直流分量。考虑到直流分量的良好性质（既可以看作周期无限短，又可以看作周期无限长），

第一点听起来有点晦涩，我们直接来看代码。

代码就像照妖镜，不管故事讲得多么动听，它总能抓住背后的核心本质。

代码：https://github.com/TsinghuaC3I/Fourier-Position-Embedding

ROPE：

def apply_rotary_pos_emb(self, sin, cos, x, inverse=False):
    # 先把最后一半维度右移（rotate-half）
    # x.shape = [..., 2*(dim//2)]
    rot = self.rotate_half(x)

    if not inverse:
        return x * cos + rot * sin
    else:
        return x * cos - rot * sin

FOPE：

def apply_rotary_pos_emb(self, sin, cos, x, inverse=False):
    # 1) 先把 sin/cos 从 (…, input_dim*2) 投影到 (…, output_dim)
    #    支持两种系数：sin_coef/cos_coef 或者 一个 fourier_coef
    fourier_sin = torch.einsum(f"{self.input_shape}, {self.coef_shape} -> {self.output_shape}",
                               sin, self.sin_coef)
    fourier_cos = torch.einsum(f"{self.input_shape}, {self.coef_shape} -> {self.output_shape}",
                               cos, self.cos_coef)
    # 2) pad 到原始 head_dim，拼接成 (…, head_dim)
    fourier_sin = torch.cat((fourier_sin, fourier_sin), dim=-1)
    fourier_cos = torch.cat((fourier_cos, fourier_cos), dim=-1)

    # 3) 再做 rotate-half + 加权
    rot = self.rotate_half(x)
    if not inverse:
        return x * fourier_cos + rot * fourier_sin
    else:
        return x * fourier_cos - rot * fourier_sin

这里采用的是einsum，其实相当于做了个线性层变换(nn.Linear(input_dim, output_dim, bias=False)。

原作回应

ROPE作者和FOPE的作者也有讨论。苏神给出的回应是”基于https://kexue.fm/archives/9403，理论上RoPE的当前形式是完备的。“