消息传递与特征变换分离的图神经网络
在研究图神经网络的鲁棒性的时候,发现消息传递和特征变化分离开会更有鲁棒性,但未找到是否有前人做过。后来我才发现这正是PPNP的结构。
PPNP
PPNP(personalized propagation of neural predictions)出自ICLR2019的《 Predict then Propagate: Graph Neural Networks meet Personalized PageRank》,简单来说就是先使用神经网络进行特征变换,最后使用pagerank来消息传播。
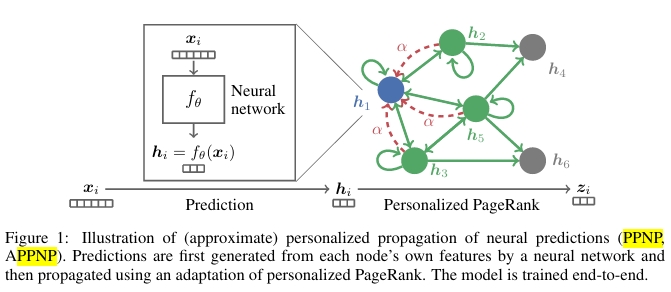
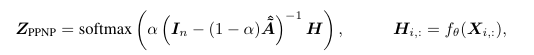
1 | |
由于有求逆步骤,会导致开销较大,又有以下近似版本。
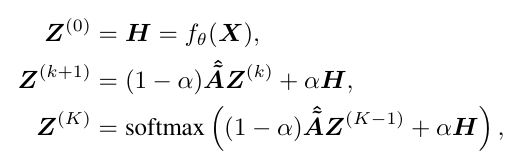
PMLP
我的想法实际上是连训练的过程中都不用邻接矩阵。
这实际上与ICLR2023的《GRAPH NEURAL NETWORKS ARE INHERENTLY GOOD GENERALIZERS: INSIGHTS BY BRIDGING GNNS AND MLPS》不谋而合。
论文中主要是从NTK的角度研究问题,模型创新性较低。
审稿人所说:Q1: “PMLP 可能不是一个新颖的方法,它可能是 APPNP 从转导到归纳设置的扩展版本。”
作者回答:确实,从模型架构的角度来看,APPNP 论文[1]中提出的用于消融研究的变体可以大致看作是 PMLP 的特殊情况(即具有 APPNP 式架构、个性化 PageRank MP 方案和残差连接)。然而,这并不削弱我们的主要贡献,因为之前尚未确定本文的核心方面,即经验发现以及理论理解。
[1]的主要贡献在于提出了 APPNP 作为新的特定 GNN 模型,并展示了其在先前 GNN 模型上的经验优势。相比之下,我们引入了 PMLP 作为一类新的模型架构,适用于大量 GNN,更重要的是,PMLP 用于分析目的,基于此,我们识别出一种普遍现象,该现象在 MP 实例化、GNN 架构、超参数等方面是一致的。除了这一新的经验发现之外,我们还利用 PMLP 作为显微镜,揭示 GNN 在节点级任务中成功的主要原因是它们在推理中使用的 MP 操作带来的固有泛化能力,这也得到了我们理论分析的证实。
关于归纳设置,请特别注意,我们并非刻意与专注于归纳设置的先前工作不同,而是为了实现公平比较(即通过使用归纳设置确保 MLP、GNN 和 PMLP 能够访问相同的训练数据信息),并使我们的结果合理且有意义。为了帮助在演示中更清晰地展示我们的整体框架,我们在第 1.1 节中增加了更多讨论,以更好地定位这项工作与先前技术的关系。
论文也只理论研究了说PMLP为什么会比MLP更好,而没有涉及到GNN。更多只是实验。
对于MLP:
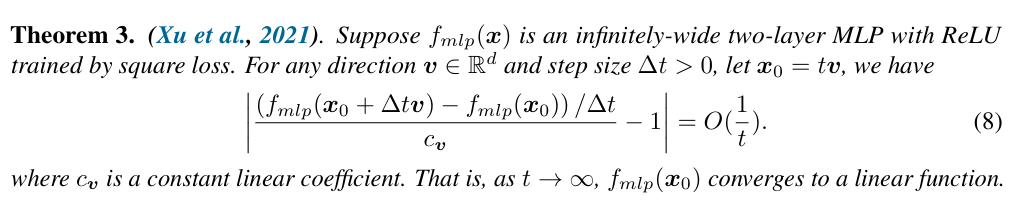
对于PMLP:
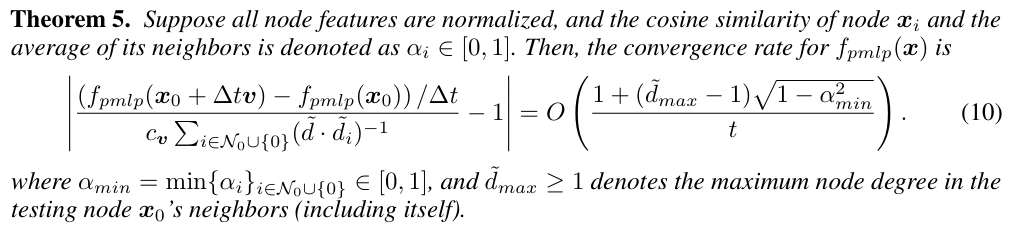
两者对比,尽管在外推情况下二者都会变为线性模型,但是可以发现PMLP的参数更多,也许会学到一个更好更平滑的表示。
正如审稿人所说:Q2: “定理 4 和 5 似乎适用于 PMLP 和原始 GNN。因此,仍然存在一个差距需要解释为什么 PMLPs 能够实现接近 GNN 的性能。”
作者回答:确实,定理 4 和 5 的目的是为了揭示“图神经网络天生具有泛化能力”的理论洞察,并解释我们关于 GNNs/PMLPs 具有优越泛化能力的实证发现,这种泛化能力源于用于推理的 GNN 架构本身,而不是严格回答“为什么用 MLP 权重替换 GNN 权重不会损害准确性”。PMLPs 和 GNNs 之间接近的性能实际上作为实证证据,使得我们的理论结果更加有力:如果权重对泛化很重要,那么在分析中“不考虑权重看起来如何”时,我们的理论结果将不那么有说服力。
尽管如此,我们确实认为理解 PMLPs 和 GNNs 之间紧密性能背后的理论基础很重要。作为第一个揭示这一现象的工作,我们也探讨了 PMLPs 在哪些情况下优于或劣于 GNNs,并进行了相应的讨论(第 3.2 节和第 5 节),这涉及到噪声边、自连接、模型表达性和未标记节点的作用。将这些因素全部纳入分析可能足以满足 GNN 理论中的另一项工作。因此,我们将这个问题留给未来的研究。我们对第 4 节开头和第 5 节的“当前局限性和展望”进行了修改,以使这一点更加清晰。
看上去算法并不创新,理论并不完善,还能得到审稿人多个8分,这个还是让我挺震惊的。