TPSS5E1 复盘
预测贴纸销量 | Kaggle — Forecasting Sticker Sales | Kaggle是我参加最久的一次TPS(2025/04/01更新: 3月又全力参加了一次,排名18/4381,排名仍达不到拿swag的名次,但成为唯二的在shakeup中留存的top选手也算差强人意。不得不说第2的chiris是真的强),但成绩不够理想,只拿到了27/2722,其中一个原因是一直参考@Cabaxiom的线性回归笔记本,但是其中年份product存在计算错误的问题。
之前TPS也有个类似的比赛,可以说是之前的翻版,所以很多solution也是参考了过去的思路。
之前的第一名方案
https://www.kaggle.com/code/ivyzang/1st-place-solution-less-is-more
EDA
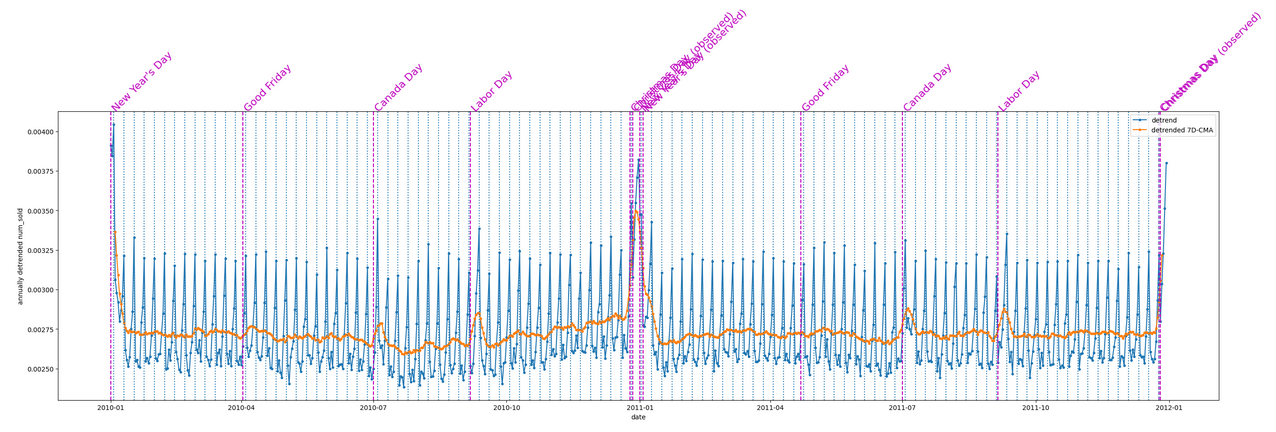
在检查商店后,发现每个商店都显示相似的销售额分布,仅差一个标量常数。
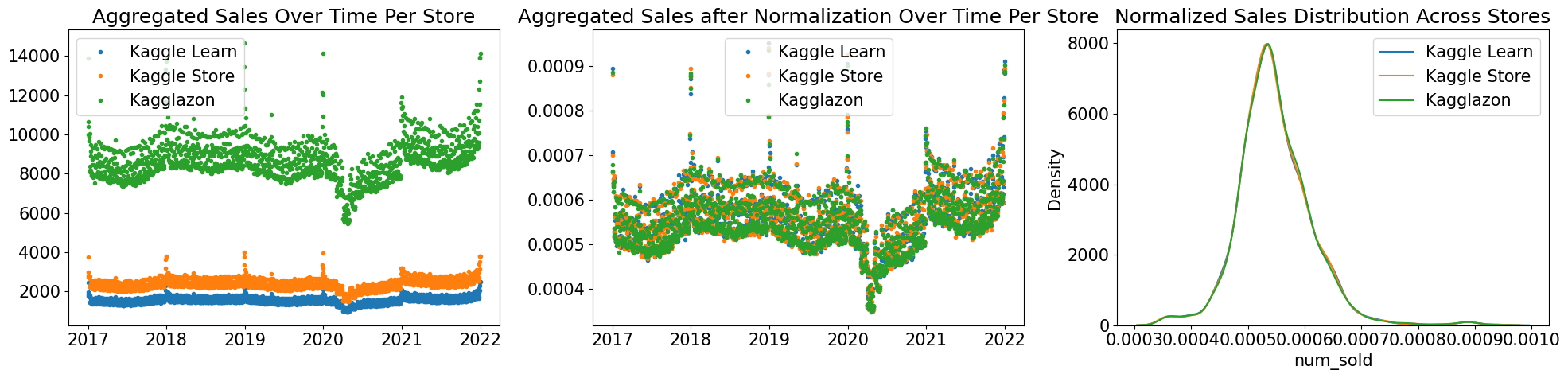
在每年的每个国家中,num_sold 都遵循着一致的规律,尽管不同国家之间的年度变化幅度有所不同。
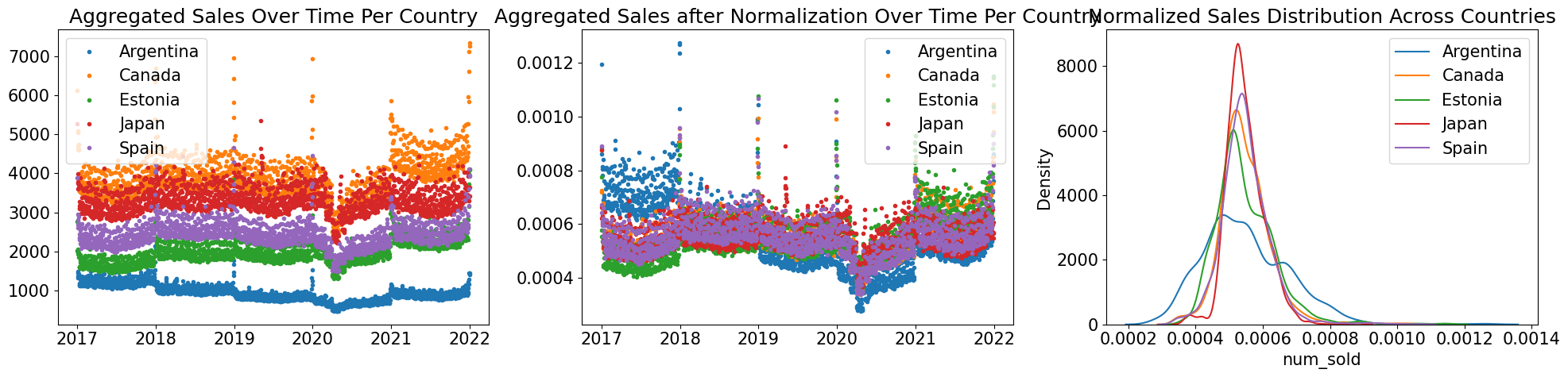
使用归一化GDP后,发现仍有显然的趋势,因此可以使用 GDP 作为外部预测因子。
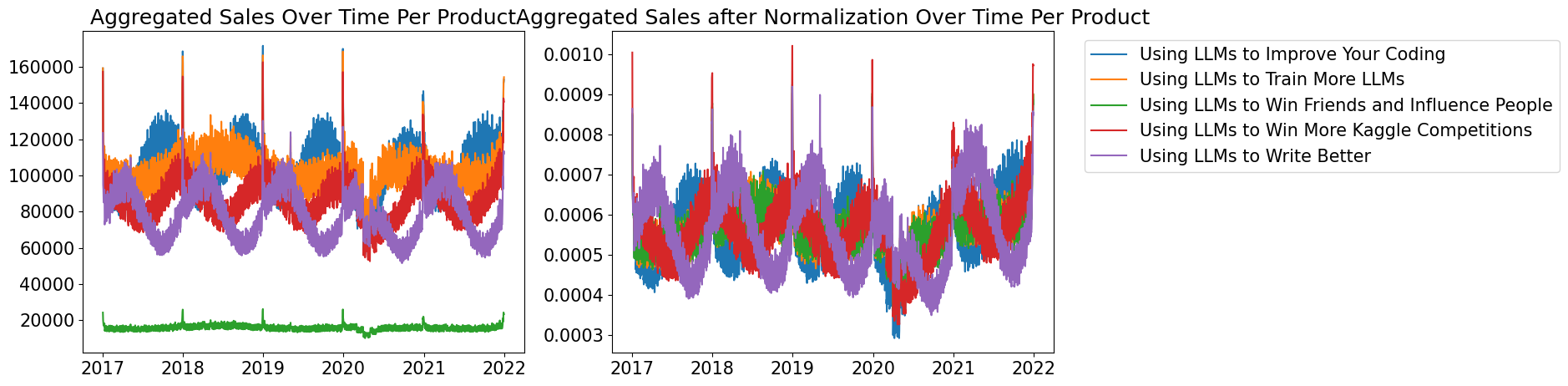
产品具有周期性。
疫情的影响。
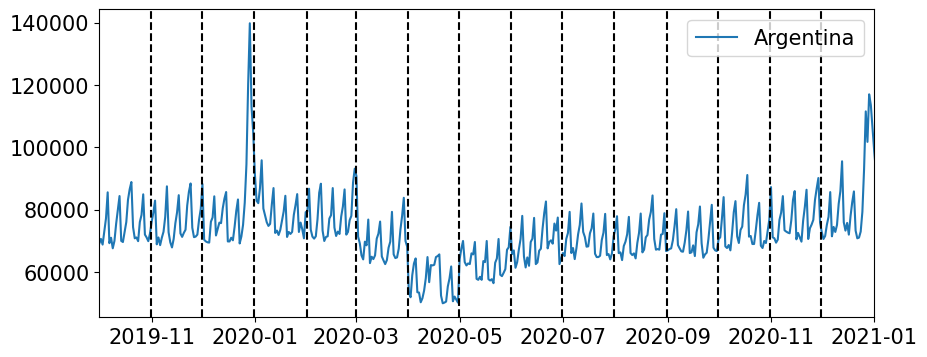
周一至周四的分布相同,而周五至周日的分布不同。
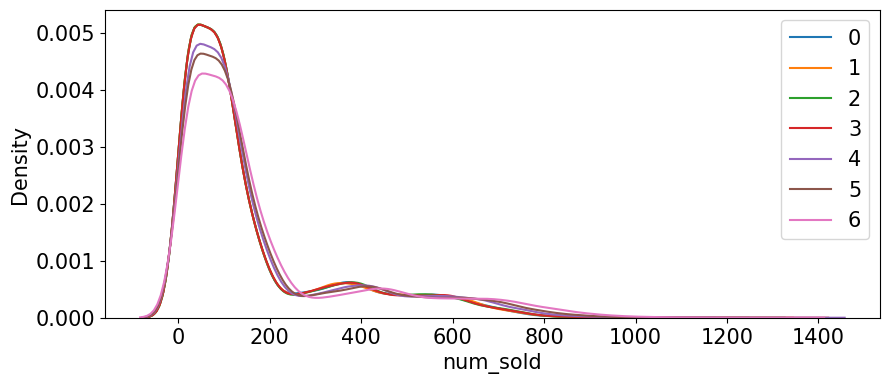
具有节假日效应(即节假日前后消费更高)。且具有后续的“圣诞节和元旦的节假日效应可能会出现覆盖或影响的情况”,作者故新建了一个新年因子。
第一轮分析
乘性线性模型:
$$
\begin{equation} \text{sold} = \text{GDP}(\text{country}, \text{year}) \times \text{const}(\text{store}) \times \left[ \text{sine/cosine waves}(\text{product}) + \text{holiday} + \text{weekday} + \text{covid} \right] \end{equation}
$$
因为是乘法所以取对数,并利用$lnx\sim x-1$,对除了GDP以外的元素做此操作。
检查残差,作者发现:年末奇怪的直线和一些奇怪的持续水平线
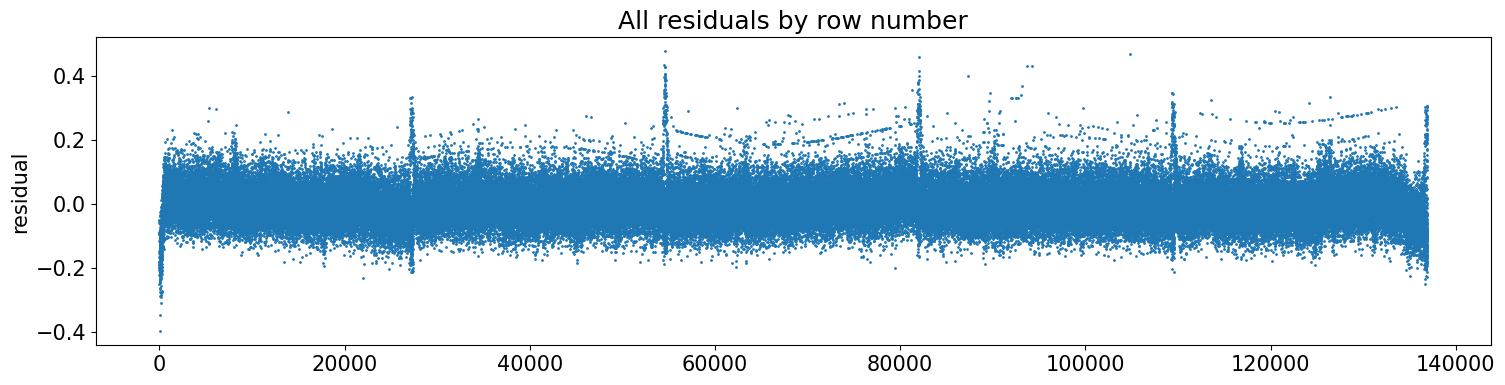
检查发现是产品’Using LLMs to Win Friends and Influence People’引起的。
继续分析数据,作者观察到 Kagglazon 的”num_sold”呈现出良好的正弦波。然而,对于阿根廷和爱沙尼亚这两个国家,Kaggle Learn 和 Kaggle Store 的”num_sold”则表现为直线。
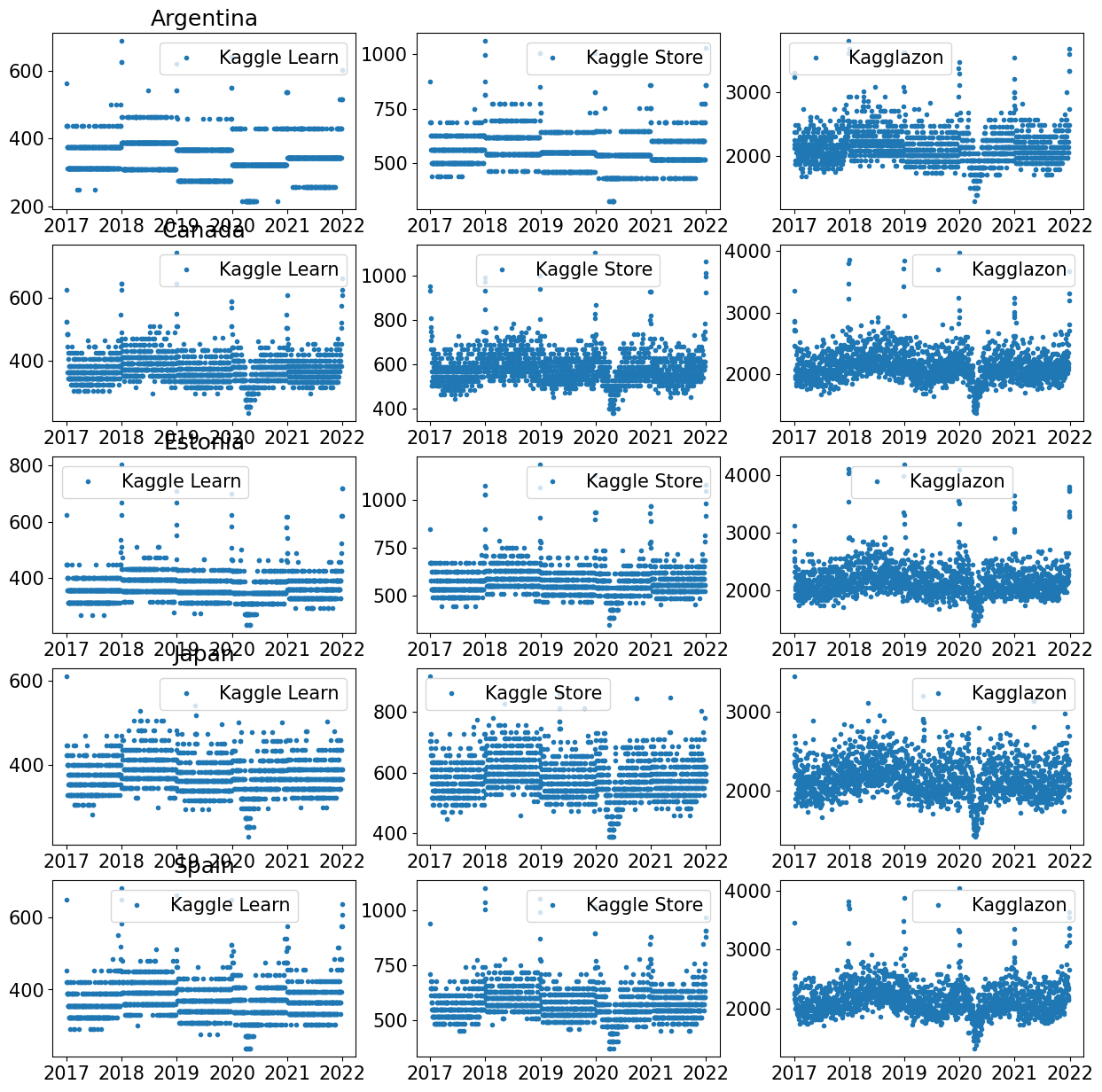
这引发了这样一个问题:这些商店是否每天都在销售相同数量的产品?作者继续深入挖掘数据。
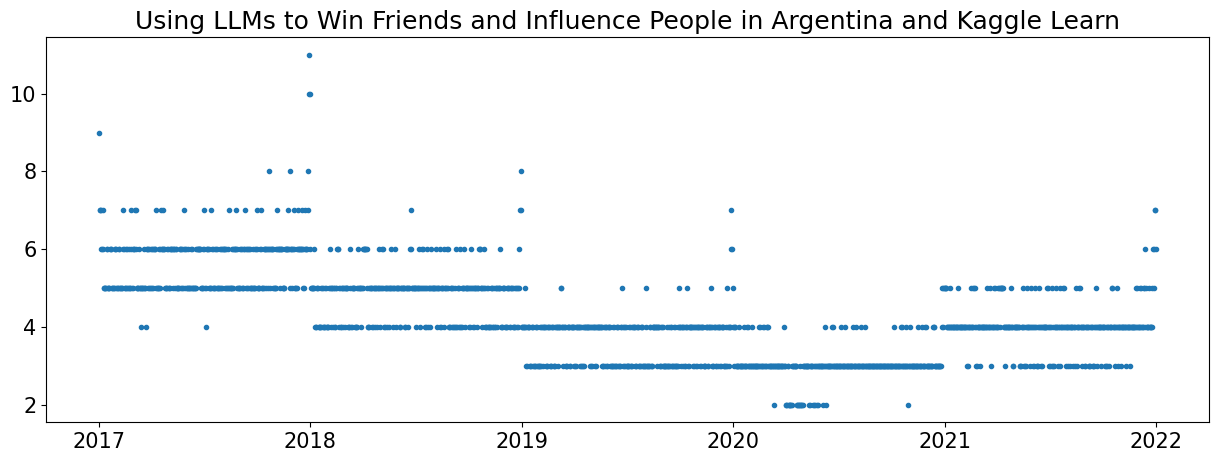
作者检查直线,发现:下面的代码从时间序列数据中识别潜在的候选国家特定假日。通过计算残差并根据国家和一年中的日期进行分组,它使用 z 分数检测显著偏差。这些偏差可能表明假日或特殊事件会影响销售模式
| country 国家 | dayfix 日修正 | residual 残差 | z_score 标准分数 | date 日期 |
|---|---|---|---|---|
| Argentina 阿根廷 | 363 | -0.068320 | -3.576392 | 2017-12-29 |
| 364 | -0.105399 | -5.517371 | 2017-12-30 | |
| 365 | -0.097595 | -5.108857 | 2017-12-31 | |
| 366 | -0.084645 | -4.430960 | 2018-01-01 | |
| Canada 加拿大 | 53 | 0.060064 | 3.144173 | 2017-02-22 |
| 54 | 0.062321 | 3.262322 | 2017-02-23 | |
| Estonia 爱沙尼亚 | 365 | -0.058432 | -3.058758 | 2017-12-31 |
| 366 | -0.062565 | -3.275110 | 2018-01-01 | |
| Japan 日本 | 1 | 0.119266 | 6.243256 | 2017-01-01 |
| 2 | 0.058107 | 3.041753 | 2017-01-02 | |
| 361 | 0.084893 | 4.443952 | 2017-12-27 | |
| 362 | 0.160301 | 8.391348 | 2017-12-28 | |
| 363 | 0.245581 | 12.855538 | 2017-12-29 | |
| 364 | 0.298412 | 15.621061 | 2017-12-30 | |
| 365 | 0.285922 | 14.967284 | 2017-12-31 | |
| 366 | 0.233630 | 12.229903 | 2018-01-01 | |
| Spain 西班牙 | 363 | -0.073186 | -3.831102 | 2017-12-29 |
| 364 | -0.107250 | -5.614233 | 2017-12-30 | |
| 365 | -0.111582 | -5.841026 | 2017-12-31 | |
| 366 | -0.086679 | -4.537431 | 2018-01-01 |
作者发现这一些天中有一些不存在假期效应,故需要从假期中移除。还发现日本不在圣诞节和新年(除 2017 年外)庆祝假期。这就是为什么在年末会有很大的残差。
另外作者还发现使用三角函数拟合周期时,只需要 sin_1/cos_1 波,而对于其他产品,只需要组合 sin_0.5 和 cos_0.5。
第二轮分析
通过第一轮,作者在这轮做了以下处理:
- 删除一些假日。移除加拿大的一些“无效”节假日(2,4,5,8,10月)。移除日本2018-12-24的特定假日。
- 新年和圣诞节排除日本
- 调整产品周期性特征
再次进行残差分析,发现仍有一些日期的残差较大。
观察到数据后,发现加拿大和爱沙尼亚在12月26日和27日有节假日。模型已经单独处理了“大”的新年假期,为避免多重共线性,打算从普通节假日列表中移除1月1日和12月25日。
假期效应用高斯分布拟合。
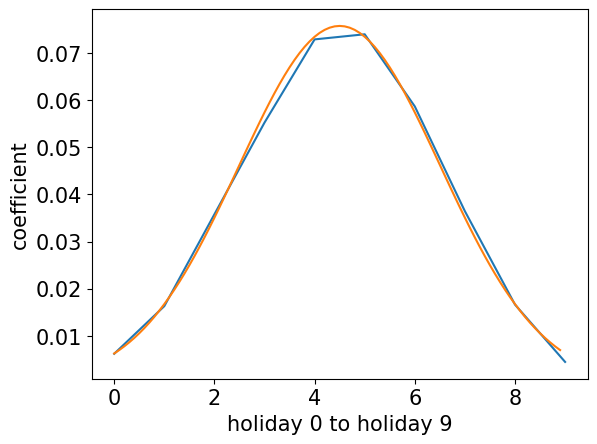
第三轮分析
- 从普通节假日列表中移除圣诞节和元旦(因为已由特殊日期特征处理)。
- 单独处理加拿大和爱沙尼亚12月26日的节假日。
- 使用高斯曲线拟合的权重来创建节假日特征(代替原来的10个0/1指示变量)
第四轮分析
绘制岭回归系数随正则化的变化,以找到最优的 alpha。
尝试移除 year_2020 参数,增加 year_2019_Dec 参数(最终发现不加这两个参数的版本在公开排行榜更好)。
尝试添加CCI(消费者信心指数)数据,但未改善CV分数。
最终提交
特征工程
日期特征: 与之前类似。
节假日特征 (df_holidays):
- 从
holidays库获取节假日。 - 移除了加拿大的一些“无效”节假日。
- 移除了所有国家(阿根廷、加拿大、爱沙尼亚、西班牙)的1月1日和12月25日(因为它们由
special_date_columns处理)。 - 移除了加拿大和爱沙尼亚的12月26日(因为它们由
holiday_1226特殊特征处理)。 - 移除了日本2018-12-24的假日。
GDP特征: 之前类似。
高斯加权节假日特征 (holiday, holiday_1226):
holiday_diff = [np.exp(-(i - 4.5) ** 2 / 8.5) for i in range(11)]:- 创建一个单一的
holiday特征。对于df_holidays中的每个节假日,其影响会根据holiday_diff的权重分布到节假日当天及之后的10天。 special_date_columns: 创建12月25-31日和1月1-10日的指示变量(日本特殊处理)。holiday_1226: 为爱沙尼亚和加拿大12月26日的节假日创建一个高斯加权特征。
周期性特征 (product_year_columns): 与第二轮类似,根据不同产品的特性选择 sin/cos_1 或 sin/cos_0.5。
COVID特征 (featured_month_columns): 2020年3-10月的月度指示变量。
其他分类特征: week_columns (周五、六、日),store_columns,product_columns (均为独热编码,去掉第一类)。
模型
使用Pipeline包含StandardScaler(标准化)和Ridge(alpha=150, tol=0.00001, max_iter=10000)(岭回归)。alpha=150是正则化强度,通过调优选择。
后处理
1 | |
数据介绍
共五列分为日期(天为单位)、country、store、product、num_sold(目标值)。
2010-2016是训练集
2017是测试集的公榜
2018-2019是测试集的私榜
EDA
@BROCCOLI BEEF指出,product具有周期性、store具有不变性、GDP和销售额具有较强相关性。
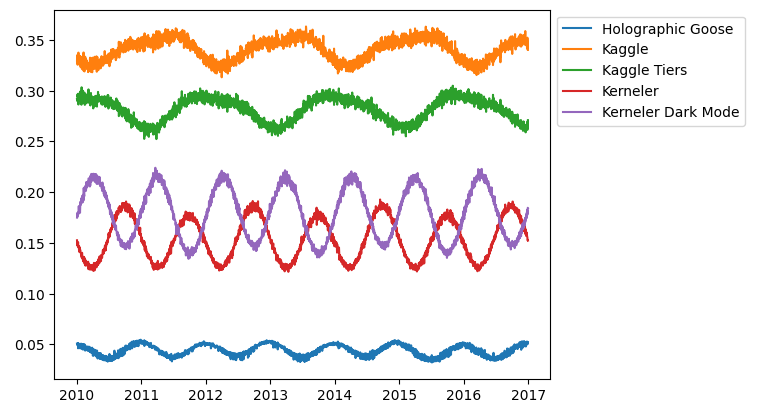
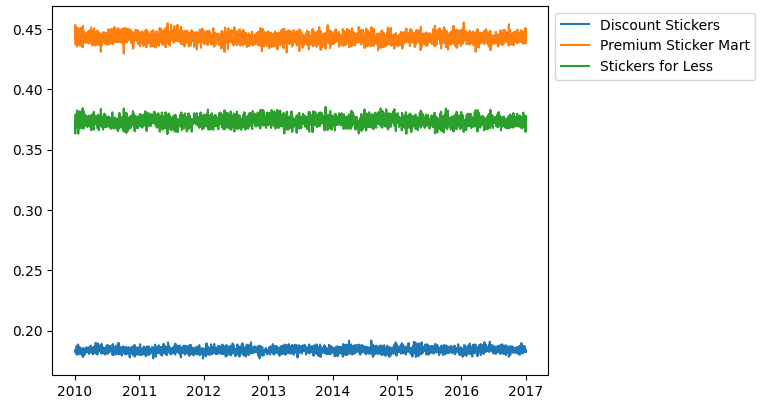
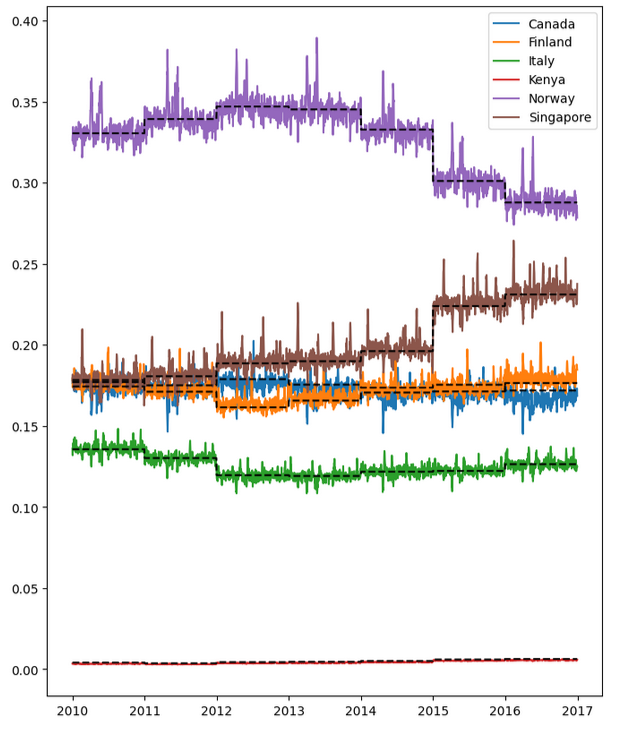
@Konstantin Dmitriev发现GDP在Kenya不符合,我和@BROCCOLI BEEF发现原因可能是因为$num_{sold}=a*GDP+bias$,而我们忽视了bias。
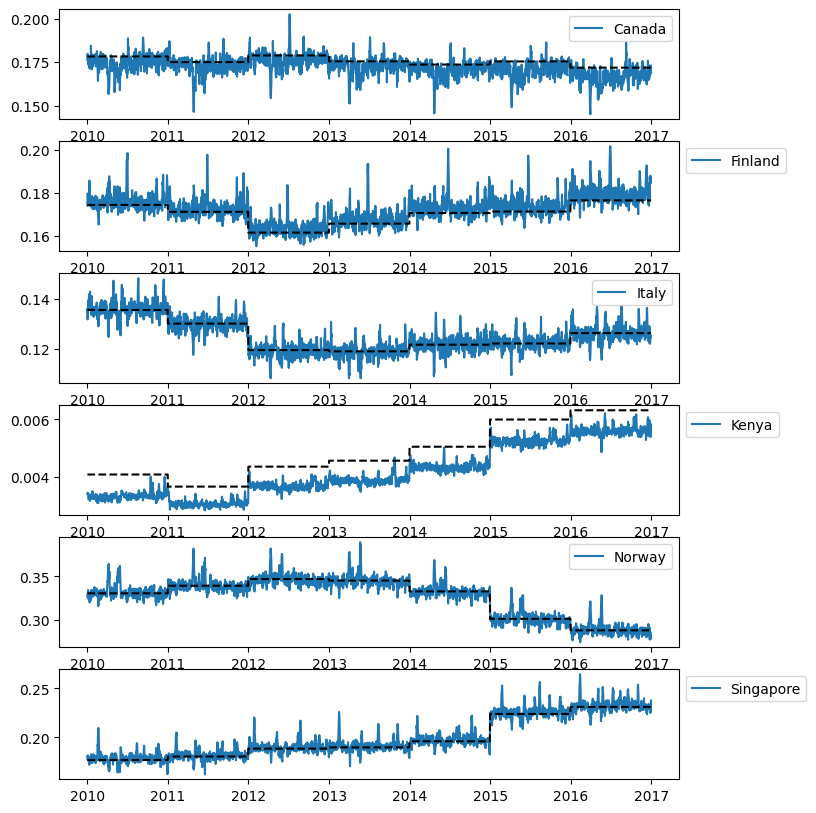
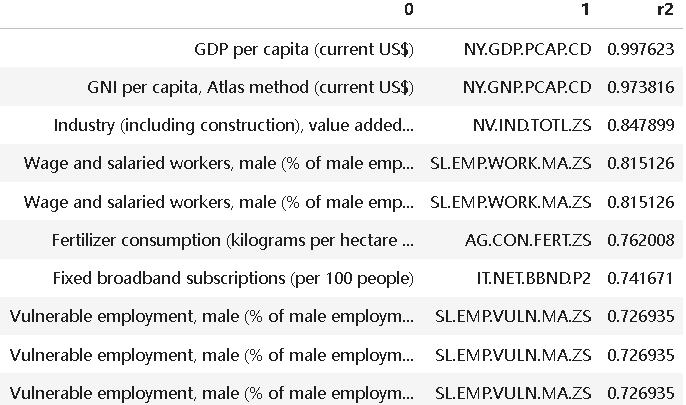
由上,我顺带分析了所有的514个世界银行特殊指标,其中GDP具有最高的R2,这也说明GDP已经足够了。
我发现,每周周日具有最多的销售额,且每周具有周期性。
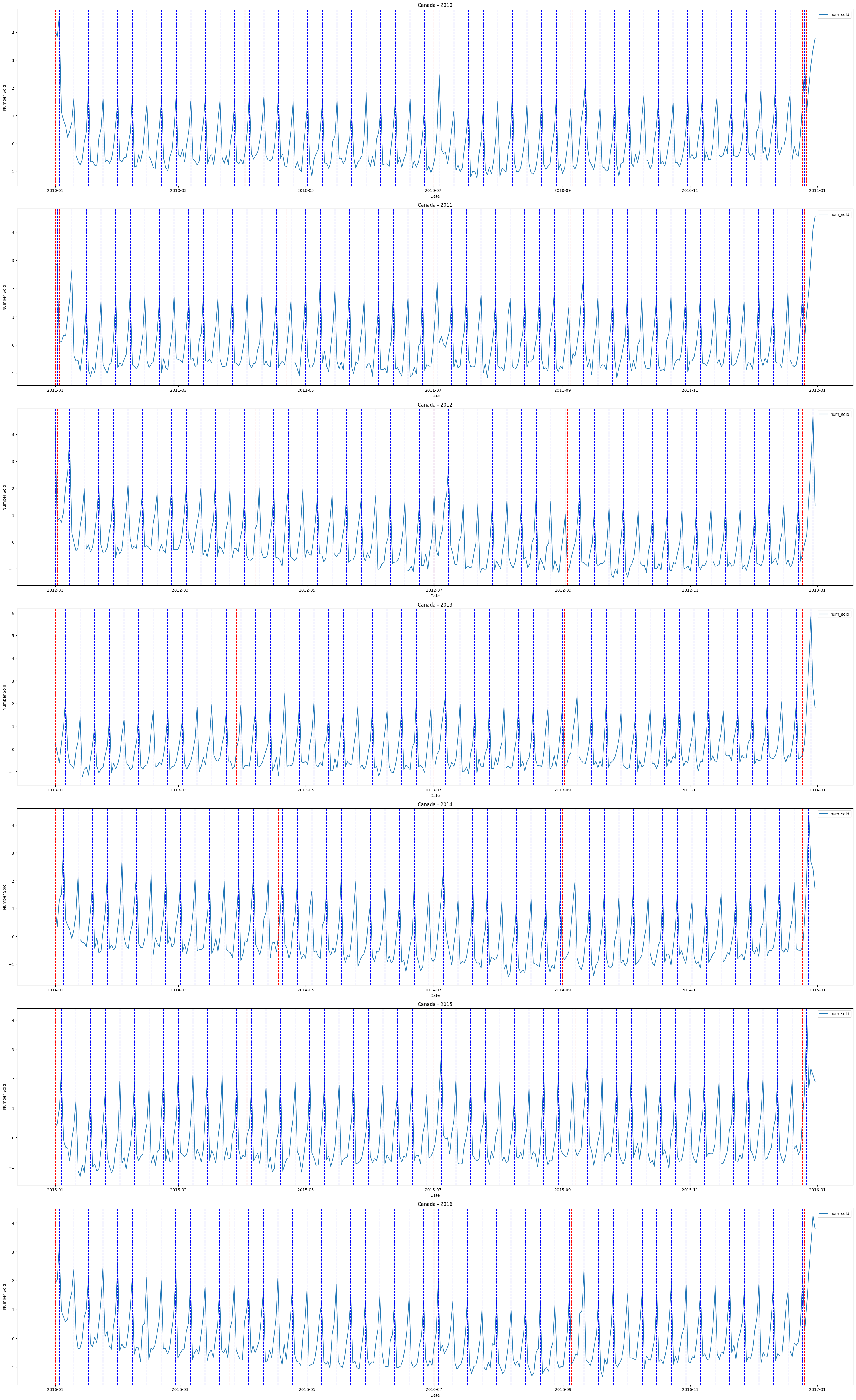
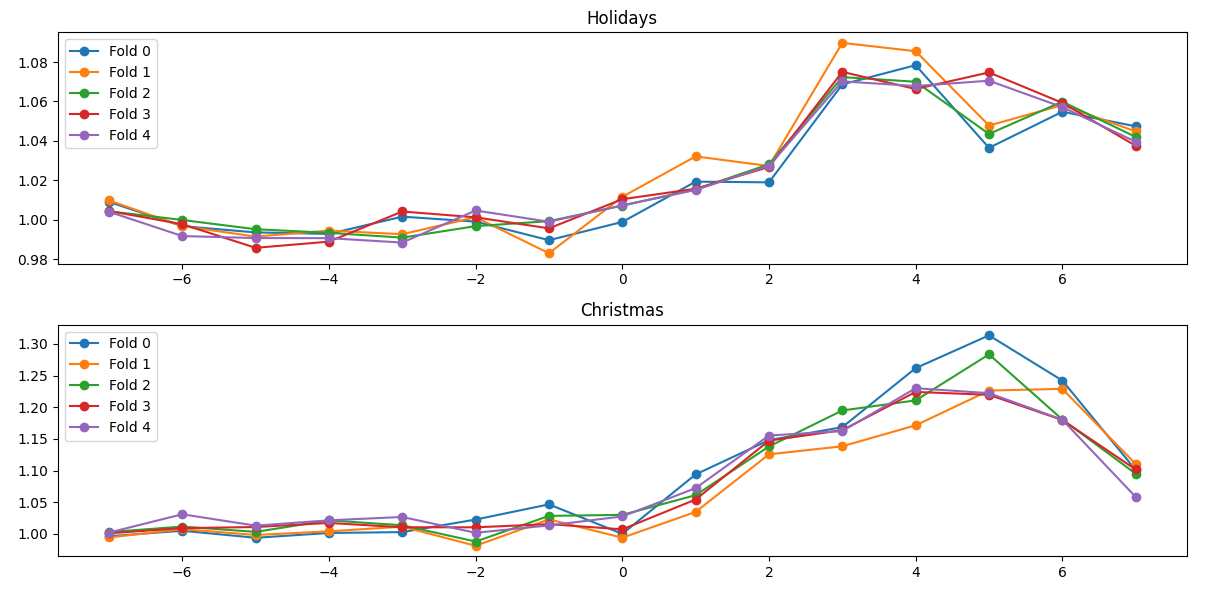
@BROCCOLI BEEF指出了节假日效应:
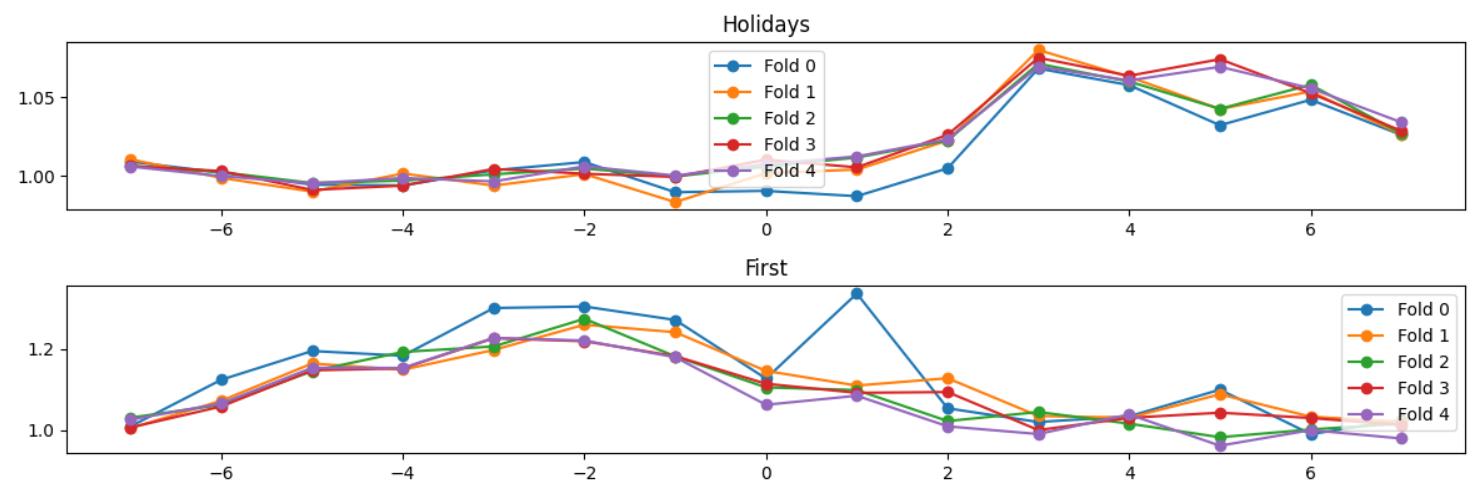
并分析了节假日效应大概的持续时间:
我指出圣诞节和元旦的节假日效应可能会出现覆盖或影响的情况:
(事实上,在比赛中,我并没有完整读完上届的第一名的solution,但是得到了不谋而合的结论)
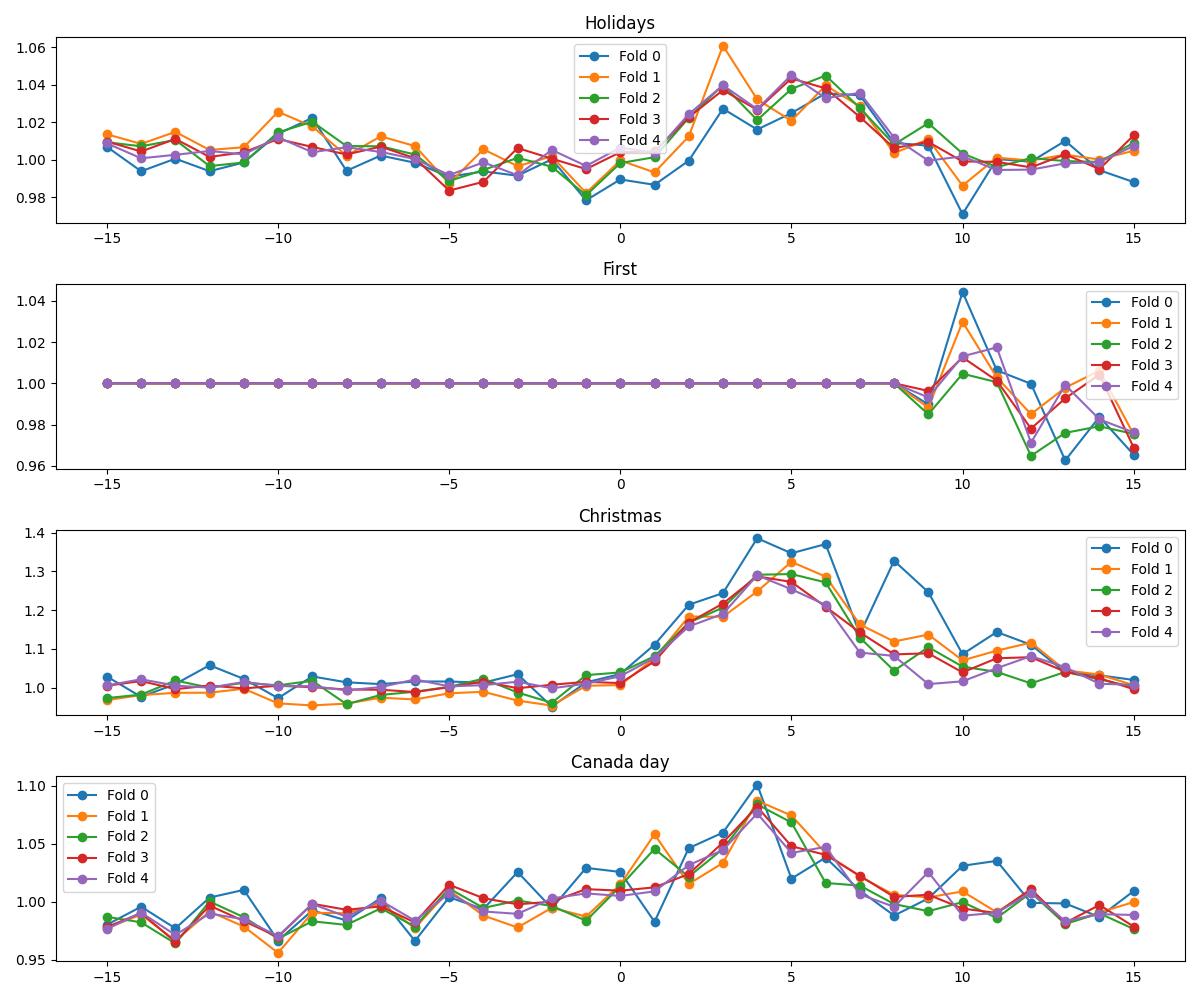
接下来,我将介绍前6的solutions(solution类似的则只叙述最高排名的solution)
其中“圣诞节和元旦的节假日效应可能会出现覆盖或影响的情况”这个性质,在前6名中,只被第一名所使用。也许这就是在高分者算法大致类似的情况下,第一名没有更多复杂的操作但能优于其他人的原因之一。
第一名 by George Koussa
类似第三名的乘性线性模型
闰年特征
正弦余弦特征
是否在节假日的十天内特征:
1 | |
gdp采用bias
1 | |
商店因子排除加拿大和肯尼亚进行考虑
通过ridge来预测未来因子:
1 | |
新年因子:为新年设置一个节假日因子,以应对“圣诞节和元旦的节假日效应可能会出现覆盖或影响的情况”。
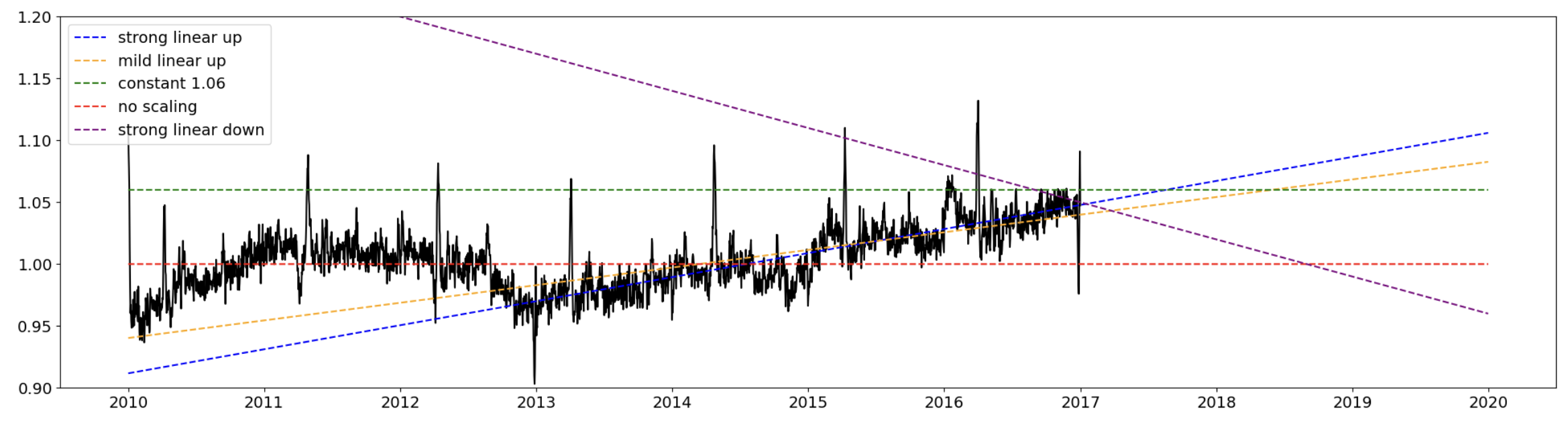
第二名 by Chris Deotte
后处理
对于未来,我们会抱有更好的态度。
所以Chris采用了两种策略,第一种是全乘以1.06,第二种是乘上1.06 + slope * (year - 2017)。
模型一
Transformer,大致代码为:
1 | |
另外:
- 在所有5个产品上训练1个模型(15个时期余弦调度)
- 添加30个布尔特征用于30个节假日
- 使用第一次预测(2017年,2018年)作为伪标签来训练第二次预测
- 使用第二次预测(2017年、2018年、2019年)作为伪标签来训练第三次预测
- 使用用不同种子训练的5个模型的中位数(用于第一次、第二次、第三次预测)
- 提交第三轮预测
事实上,我另外设计了一套大卷积核神经网络和类似FITS的傅里叶网络优于Chris的transformer模型,不过可惜没有像chris做那么多操作,使得最终分数并不是很好。
模型二
类似第三名的乘性线性模型
ensemble
通过在transformer上叠加线性回归来预测残差
第三名 by Konstantin Dmitriev
假期效应,同样使用高斯曲线来描述:
$$
H(t)=exp(-\frac{(d-d_h-d_0)^2}{2\sigma_0^2})
$$
后处理
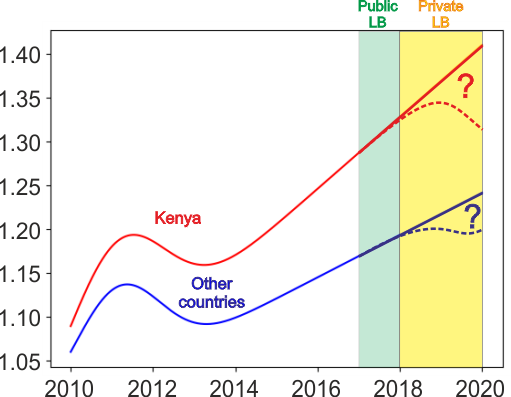
使用$trend(d)=1+s*ReLU(d-d1)$来描述,其中s和$d_1$是斜率和位移参数。
模型
乘性线性模型(部分地方使用Lasso,而不是Ridge)
我曾在论坛率先指出Lasso在某些地方会有更好的结果。
引入了day-of-year的因子
使用scipy.optimize.minimize 来优化MAPE
给每个国家都训练一个模型,具体而言:
1 | |
第六名 by Pascal Terpstra
第一个模型是@kdmitrie 发布的公共笔记本的改编。第二个模型使用的是乘性线性回归模型,第三个模型是@cdeotte 发布的 transformer。
对三者进行ensemble。