ARIMA
ARIMA 模型,全称为自回归整合移动平均模型 (Autoregressive Integrated Moving Average model)。
ARIMA 模型通常表示为 $ARIMA(p, d, q)$,其中:
- p (自回归阶数 - Autoregressive Order): 模型中包含的滞后观测值的数量,即当前值与多少个过去值相关。
- d (差分阶数 - Degree of Differencing): 使时间序列达到平稳状态所需的差分次数。
- q (移动平均阶数 - Moving Average Order): 模型中包含的滞后预测误差项的数量,即当前值的预测误差与多少个过去的预测误差相关。
AR
自回归 (AR) 部分的思想是,时间序列中当前的值 $Y_t$ 可以用其过去若干个时刻的值的线性组合来表示。
一个典型的例子,即使用过去几天的平均作为预测。
我们可以扩展为一个线性模型。对于一个 $p$ 阶的自回归模型,记作 $AR(p)$,其数学表达式为:
$$
Y_t = c + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \dots + \phi_p Y_{t-p} + \varepsilon_t
$$
其中:
- $Y_t$ 是时间序列在时刻 $t$ 的值。
- $c$ 是一个常数项。
- $\phi_1, \phi_2, \dots, \phi_p$ 是自回归系数,表示过去值对当前值的影响程度。
- $Y_{t-1}, Y_{t-2}, \dots, Y_{t-p}$ 是过去 $p$ 个时刻的时间序列值。
- $\varepsilon_t$ 是在时刻 $t$ 的白噪声误差项,通常假定其均值为0,方差恒定,且相互独立。
差分
差分 (I) 部分指的是通过差分 (Differencing) 来处理时间序列中的非平稳性。
可能听起来很玄乎。我们可以通过一个例子来理解。
比如对三角函数:
$$
\begin{align}
sin(x)&: Amplitude=1, T=2\pi
\\sin(x)-sin(x-0.2)&: Amplitude=2sin(\frac{1}{10}), T=2\pi
\\(sin(x+0.2)-sin(x))-(sin(x)-sin(x-0.2))&: Amplitude=2^2sin^2(\frac{1}{10}), T=2\pi
\end{align}
$$
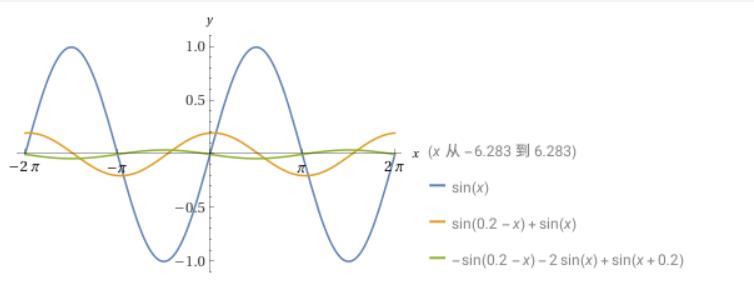
多次差分可以接近于平稳序列。
参数 $d$ 表示使原始序列达到平稳状态所需的差分次数。如果序列已经是平稳的,则 $d=0$,模型就变成了 ARMA(p,q) 模型。
MA
移动平均 部分与 AR 部分不同,它不是直接使用过去观测值的线性组合,而是使用过去预测误差的线性组合来预测当前值。一个 $q$ 阶的移动平均模型,记作 $MA(q)$,其数学表达式为:
$Y_t = \mu + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2} + \dots + \theta_q \varepsilon_{t-q}$
其中:
- $Y_t$ 是时间序列在时刻 $t$ 的值。
- $\mu$ 是序列的均值。
- $\varepsilon_t$ 是当前的白噪声误差项。
- $\theta_1, \theta_2, \dots, \theta_q$ 是移动平均系数,表示过去的预测误差对当前值的影响程度。
- $\varepsilon_{t-1}, \varepsilon_{t-2}, \dots, \varepsilon_{t-q}$ 是过去 $q$ 个时刻的预测误差项。
简单来说,MA 模型假设当前值受到过去随机冲击或预测误差的影响。 例如,如果昨天的预测过于乐观(即 $\varepsilon_{t-1}$ 为负),模型可能会在今天的预测中进行调整。参数 $q$ 的选择决定了模型考虑多少个历史预测误差项。
滞后算子
将 AR、I、MA 三个部分结合起来,就构成了 $ARIMA(p,d,q)$ 模型。如果一个时间序列 $Y_t$ 经过 $d$ 次差分后得到平稳序列 $W_t = \Delta^d Y_t$,并且 $W_t$ 服从一个 $ARMA(p,q)$ 模型,那么原始序列 $Y_t$ 就服从 $ARIMA(p,d,q)$ 模型。
$W_t$ 的 $ARMA(p,q)$ 模型可以表示为:
$W_t = c + \phi_1 W_{t-1} + \dots + \phi_p W_{t-p} + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q}$
或者更紧凑地使用 $B$ (其中 $B^k Y_t = Y_{t-k}$):
$(1 - \phi_1 B - \dots - \phi_p B^p)(1-B)^d Y_t = c + (1 + \theta_1 B + \dots + \theta_q B^q)\varepsilon_t$
其中 $\Phi(B) = (1 - \phi_1 B - \dots - \phi_p B^p)$ 是自回归算子多项式,$\Theta(B) = (1 + \theta_1 B + \dots + \theta_q B^q)$ 是移动平均算子多项式。
如何确定模型的阶数 (p, d, q)
这是 ARIMA 建模中最关键且最具挑战性的一步,通常遵循 Box-Jenkins 方法论:
a. 确定差分阶数 $d$:
- 单位根检验 (Unit Root Tests):
- ADF 检验 (Augmented Dickey-Fuller test): 原假设是序列存在单位根 (非平稳),备择假设是序列不存在单位根 (平稳)。如果 p-value 小于显著性水平 (如0.05),则拒绝原假设,认为序列平稳。
- KPSS 检验 (Kwiatkowski-Phillips-Schmidt-Shin test): 原假设是序列平稳,备择假设是序列非平稳。
- 自相关函数 (ACF) 图: 对于非平稳序列,ACF 图通常会缓慢衰减,而不是快速截尾。
通常进行一阶差分,然后再次检验平稳性。如果仍不平稳,可以尝试二阶差分。但一般情况下, $d$ 的取值不会超过 2。过度差分会导致模型引入不必要的复杂性。
b. 确定自回归阶数 $p$ 和移动平均阶数 $q$:
在序列平稳化 (即确定了 $d$ 之后,对差分后的序列 $W_t$) 后,使用自相关函数 (ACF) 和偏自相关函数 (PACF) 图来初步判断 $p$ 和 $q$ 的值。
- ACF (Autocorrelation Function): 度量序列与其自身滞后值之间的相关性。
- PACF (Partial Autocorrelation Function): 度量在控制了中间滞后项影响后,序列与其自身滞后值之间的相关性。
常见的判断规则:
| 模型类型 | ACF 图特征 | PACF 图特征 |
|---|---|---|
| AR(p) 模型 | 拖尾 (geometrically decaying or damped sine wave) | $p$ 阶后截尾 (cuts off after lag p) |
| MA(q) 模型 | $q$ 阶后截尾 (cuts off after lag q) | 拖尾 (geometrically decaying or damped sine wave) |
| ARMA(p,q) 模型 | 拖尾 | 拖尾 |
- 截尾 (Cuts off): 指相关系数在某个滞后阶数后突然变为0或在零附近小幅波动 (在置信区间内)。
- 拖尾 (Tails off): 指相关系数逐渐衰减至0,而不是突然截断。
如果 ACF 和 PACF 都显示拖尾,则可能是一个 ARMA(p,q) 模型,此时 $p$ 和 $q$ 的具体值可能需要尝试不同的组合,并结合信息准则 (如 AIC, BIC) 来选择。
ARIMA 模型的建模步骤 (Box-Jenkins 方法论)
模型识别 (Identification):
- 绘制时间序列图,检查平稳性。
- 进行单位根检验 (如 ADF 检验) 确定差分阶数 $d$。
- 对差分后的平稳序列绘制 ACF 和 PACF 图,初步判断 $p$ 和 $q$ 的可能取值。
参数估计 (Estimation):
- 根据识别出的 $p, d, q$ 值,估计模型中的参数 ($\phi_i, \theta_j, c$)。常用的估计方法是最大似然估计 (MLE) 或最小二乘估计。
模型诊断 (Diagnostic Checking):
- 残差分析: 检验模型的残差序列是否为白噪声。
- 绘制残差的 ACF 和 PACF 图,看是否存在显著的自相关。理想情况下,残差的 ACF 和 PACF 图应该在所有滞后阶数上都没有显著的相关性。
- 进行 Ljung-Box 检验 (或 Box-Pierce 检验),原假设是残差序列为白噪声。如果 p-value 较大,则不能拒绝原假设,说明模型拟合良好。
- 参数显著性检验: 检验估计出的参数是否显著不为零 (通常看 t 统计量或 p-value)。不显著的参数可以考虑从模型中剔除。
- 信息准则: 比较不同阶数组合 (p,q) 的模型,选择 AIC (Akaike Information Criterion) 或 BIC (Bayesian Information Criterion) 值最小的模型。这些准则在模型拟合优度和模型复杂度之间进行权衡。
- 残差分析: 检验模型的残差序列是否为白噪声。
模型预测 (Forecasting):
- 如果模型通过了诊断检验,就可以用来对未来的时间序列值进行预测。可以生成点预测和区间预测。