图卷积等价于mixup
(TMLR 2024)《On the Equivalence of Graph Convolution and Mixup 》
图卷积等价于mixup
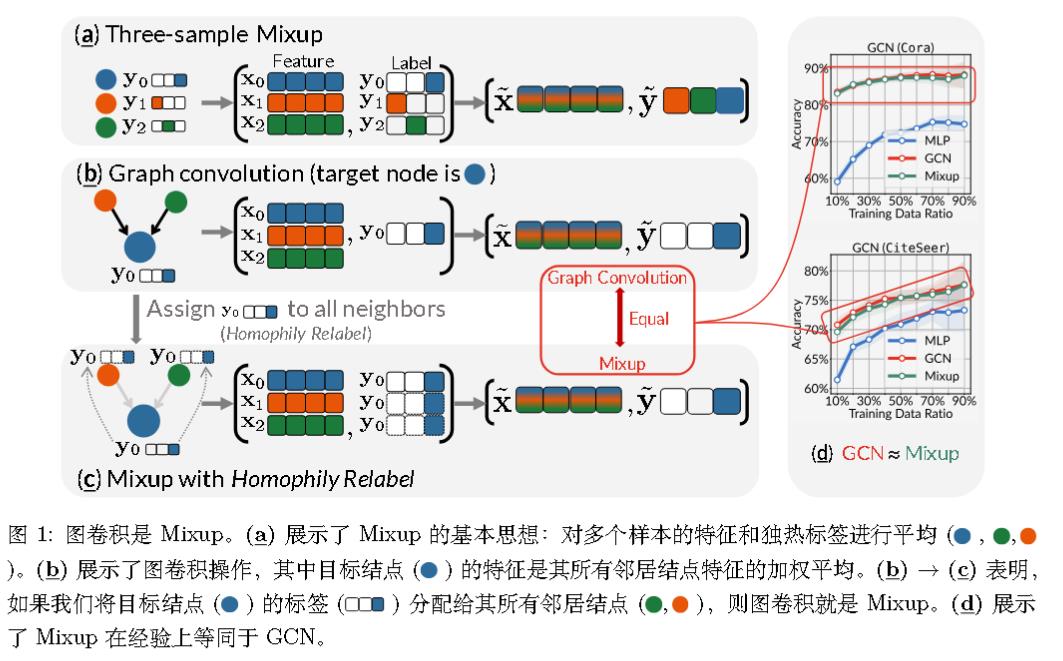
图卷积实际上是对邻居进行平均,即可以写成:
$$
(\hat{x},\hat{y})=\left(\frac{1}{|N_i|}\sum_{k\in N_i}x_k,y_i\right)
$$
而mixup实际上也是一种平均,即:
$$
(\hat{x},\hat{y})=\left(\sum_{i=1}^N \lambda_ix_i,\sum_{i=1}^N \lambda_iy_i\right)
$$
图卷积等价于训练时+测试时使用mixup
在以上的基础,作者进一步提出,图卷积等价于训练时+测试时使用mixup,即Homophily Relabel and Test-time Mixup。
Homophily Relabel
1)使用混合标签 $\hat Y=AY$重新标记图中的所有结点。
这其实就是标签传播(Label Propagation)。
2)在重标后的图上,仅利用结点特征,使用$\hat Y$对所有结点使用MLP训练。
作者把它命名为HMLP。
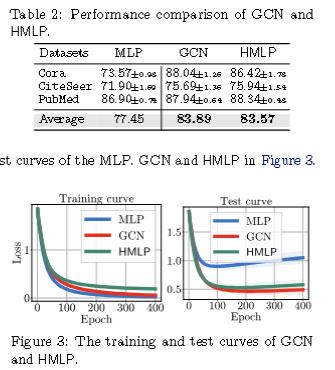
Test-time Mixup
1)仅使用训练集的结点特征来训练一个 MLP。
2)在测试期间,利用训练好的 MLP 进行推理,并结合邻居聚合。
作者把它命名为TMLP。
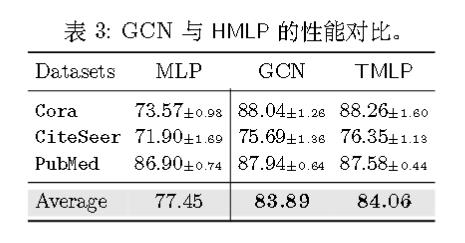
统一二者
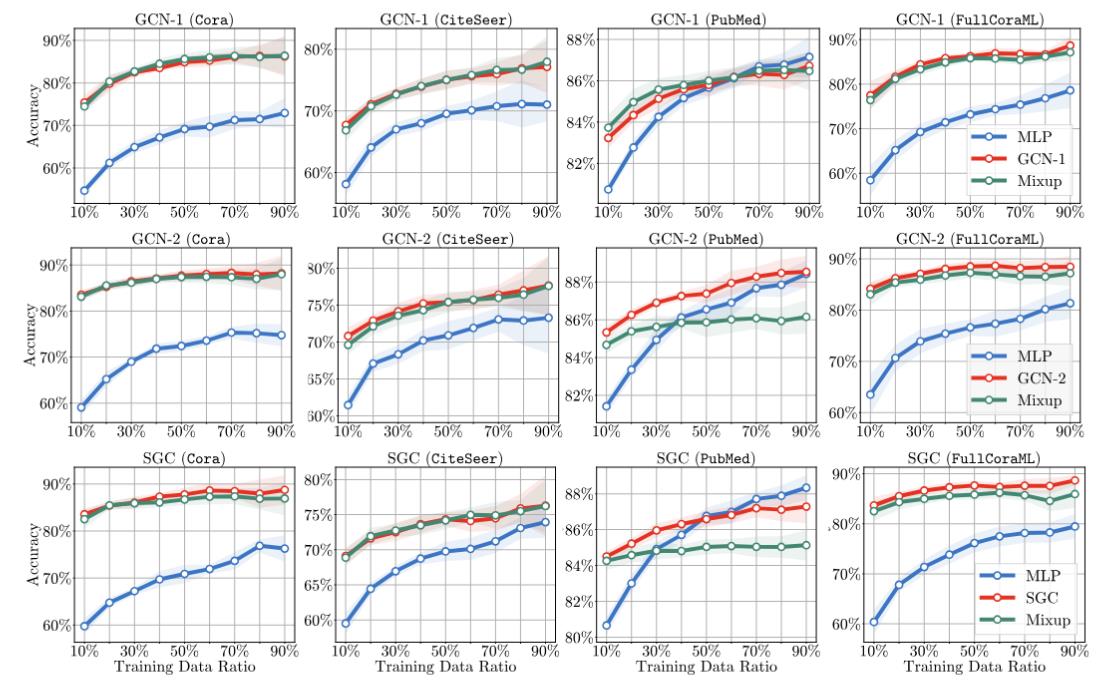
图卷积等价于mixup
https://lijianxiong.space/2024/20241006/