RNN与注意力
2014年,Volodymyr的《Recurrent Models of Visual Attention》一文中首先将注意力其应用在视觉领域,后来伴随着2017年Ashish Vaswani的《Attention is all you need》中Transformer结构的提出,注意力机制大成。
在注意力机制中,除去耳熟能详的SENet和CBAM,也有一些主动去学习注意区域的网络算法。
比如以下两篇,都出自deepmind。
《MULTIPLE OBJECT RECOGNITION WITH VISUAL ATTENTION》ICLR 2015
《DRAW: A Recurrent Neural Network For Image Generation》


DRAM
模型架构:
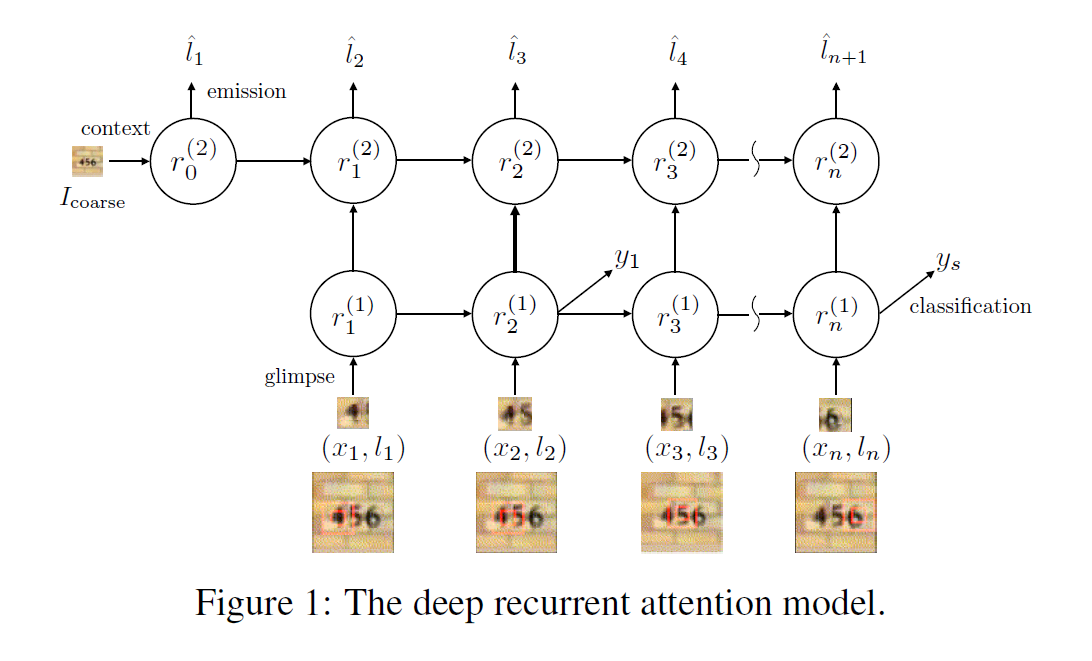
Glimpse Network**
该网络是一种非线性函数,接收当前输入的图像patch或者说是glimpse,$x_n$,以及其位置序列$l_n$,其中$l_n=(x_n,y_n)$作为输入,输出一个向量$g _ {n}$。
Glimpse Network 的工作就是从原始图像中从位置$l _ {n}$附近提取一组有用的特征。利用$G _ {image}(x_n|W _ {image})$来表示函数$G _ {image}(\dot)$的输出向量$G _ {image}(\dot)$的输入是图像patch $x_n$,然后以权重$W_image${参 数 化 },$G _ {image}( \dot )$ 通常由三个卷积隐层构成,没有pooling layer,然后紧跟着一个全连接层。
另外,$G _ {loc}(l _ {n}|W _ {loc})$利用全连接的隐层来映射出位置元组,$G _ {loc}(l _ {n}|W _ {loc})$ 和$G _ {image}(x_n|W _ {image})$拥有相同的维度。
我们将这两个向量进行点乘操作得到最终的 glimpse feature vector $g_n:$
$$g _ {n}=G _ {image}(x _ {n}|W _ {image})G _ {loc}(l_n|W _ {loc}).$$
Recurrent Network
RN汇聚从每一个glimpse上提取的信息,并且以一种 coherent manner组合起来以保存空间信息。
从 glimpse Network 得到的glimpse feature vector $g_n$作为每一个时刻 RN的输入。RN 由两个循环层和非线性函数$R _ {recur}$构成,定义两个 recurrent layer的输出为$r^{(1)}$ and $r^{(2)}:$
$$
\begin{align}
r^{(1)}=R _ {recur}(g_n,r _ {n-1}^{(1)}|W _ {r1})\\
r^{(2)}=R _ {recur}(g_n,r _ {n-1}^{(2)}|W _ {r2})
\end{align}
$$
我们用LSTN单元来处理非线性$R _ {recur}$,因为其具有学习长期依赖(long-range dependencies)和稳定的学习动态(stable learning dynamics)的能力。
Emission Network
该网络将RN当前的状态作为输入,然后预测出 glimpse network 应该向何处提取图像patch。这个就像一个指挥中心,从 RN 中基于当前的内部状态,控制着attention。由一个全连接隐层构成,将feature vector $r_n^{(2)}$从recurrent layer的顶部映射成坐标元组$l _ {n+1}:$
$$
\hat{l} _ {n+1}=E(r_n^{(2)}|W_e)
$$
Context Network
Context Network 提供了RN的输出状态,其输出用于 emission Network 来预测第一个glimpse的位置。Context Network $C(*)$ 将下采样的图像 $I _ {coarse}$作为输入,并且出书一个固定长度的向量$c_I$。该结构信息提供了一个可见的提示,即:所给图像潜在的感兴趣区域的位置。采用三个卷积层将粗糙的图像$I _ {coarse}$映射成特征向量作为 RN 的top recurrrent layer $r^2$ 的初始状态。底层 $r^{1}$初始化为零向量,原因后面会具体介绍。
Classification Network
分类网络基于底层RN的最终的特征向量 $r _ {N}^{(1)}$预测出一个类别标签y。由一个全连接隐层和softmax 输出层构成:
$$P(y|I)=O(r_n^1|W_o)$$
理想情况下,深度循环attention model 应该学习去寻找对分类物体相关的位置。Contextual information的存在,提供了一个”short cut”的解决方案,使得模型通过组合不同glimpse的信息从而更加容易学习到Contextudl information。
我们阻止如此不想要的行为,通过链接 context network and classification network 到不同的 recurrent layer。所以,最终使得contextual information 不能被直接用于 classification network,然后只影响模型产生的glimpse locations序列。
给定一张图像 I 的类别标签 y,我们可以利用交叉熵目标函数,将学习过程规划为 有监督分类问题。attention model 基于每一个 glimpse 得到潜在的位置变量 l,然后提取出对应的patches。所以我们可以通过忽略 glimpse locations 来最大化 类别标签的似然性 :
$$
logp(y|I,W)=log\sum _ {l}p(l|I,W)p(y|l,I,W)
$$
忽略的目标函数可以通过其 variational free energy lower bound F 来学到:
$$
\begin{align}\log\sum _ {l}p(l|I,W)p(y|l,I,W)&\geq\sum _ {l}p(l|I,W)\log p(y,l|I,W)+H[l]\\&=\sum _ {l}p(l|I,W)\log p(y|l,I,W)
\end{align}
$$
将上述函数求关于模型参数W的导数,可以得到学习的规则:
$$
\begin{align}\frac{\partial\mathcal{F}}{\partial W}
&=\sum _ {l}p(l|I,W)\frac{\partial\log p(y|l,I,W)}{\partial W}+\sum _ {l}\log p(y|l,I,W)\frac{\partial p(l|I,W)}{\partial W}
\\&=\sum _ {l}p(l|I,W)\left[\frac{\partial\log p(y|l,I,W)}{\partial W}+\log p(y|l,I,W)\frac{\partial\log p(l|I,W)}{\partial W}\right]\end{align}
$$
在glimpse 序列中的每个glimpse,很难在训练中估计许多成指数式glimpse
locations。上面公式的和可以利用蒙特卡罗采样(Monte Carlo Samples)的方法来进行
估计:
$$
\tilde{l}^m\sim p(l_n|I,W)=\mathcal{N}(l_n;\hat{l}_n,\Sigma)
$$
$$
\frac{\partial\mathcal{F}}{\partial W}\approx\frac{1}{M}\sum _ {m=1}^{M}\left[\frac{\partial\log p(y|\tilde{l}^m,I,W)}{\partial W}+\log p(y|\tilde{l}^m,I,W)\frac{\partial\log p(\tilde{l}^m|I,W)}{\partial W}\right]
$$
上面第二个公式提供了一种实际的算法来训练深度attention model。即,在每次glimpse 之后,我们从模型中预测出的glimpse location中进行采样。这些样本然后用于标准的后向传播来得到当前模型参数的估计。似然性$logp(y|l^m,I,W)$有一个unbounded range,可以在梯度估计中引入大量的 high variance。特别是,当图像中采样的位置偏离物体时,log 似然性会引入一个不想要的较大的梯度更新,并且通过剩下的模型进行后向传播。
我们可以减小公式中的 variance,通过将$logp(y|l^{m},I,W)$替换为 0/1离
散指示函数 R,然后利用一个baseline technique 来解决该问题:
$$
\begin{align}
R=\begin{cases}
1\quad y=\arg\max_y\log p(y|\tilde{l}^m,I,W) \\
0\quad \text{otherwise}
\end{cases}
\\
b_n=E _ {baseline}(r_n^{(2)}|W _ {baseline})
\end{align}
$$
像所展示的那样,recurrent network state vector $r_n^{(2)}$用来估计每一个glimpse 基于状态的baseline $b$,此举明显的改善了学习的效率。该baseline 有效地中心化了随机变量 R,并且可以通过向期望的R值讲行回归而学习到。给定指示函数和baseline,我们有如下的梯度更新:
$$
\dfrac{\partial\mathcal{F}}{\partial W}\approx\dfrac{1}{M}\sum\limits _ {m=1}^{M}\left[\dfrac{\partial\log p(y|\tilde{l}^m,I,W)}{\partial W}+\lambda(R-b)\dfrac{\partial\log p(\tilde{l}^m|I,W)}{\partial W}\right]
$$
其中,超参数$\lambda$平衡了两个梯度成分的尺度。实际上,通过利用 0/1指示函数,上式的学习规则就等价于利用强化学习的方法来训练attention model。当看作是强化学习更新时,公式13的第二项就是基于glimpse policy的期望奖励R的对应W的梯度无偏估计。(原文:the second term in equation 13 is an unbiased estimate of the gradient with respect to W of the expected reward R under the model glimpse policy。)
在推理的过程中,前馈位置估计可以用作位置坐标的决策性估计,以此提取模型下一个输入图像patch。该模型表现的像一个常规的前馈网络。我们的marginallized objective function equation 5 通过利用位置序列的采样,提供了一个预测期望的类别估计,并且对这些估计进行平均:
$$
\mathbb{E}_l[p(y|I)]\approx\frac{1}{M}\sum _ {m=1}^Mp(y|I,\tilde{l}^m)
$$
通过平均分类估计,这允许attention model 可以多次评价。作者的实验表明平均 log 概率可以得到最优的性能。
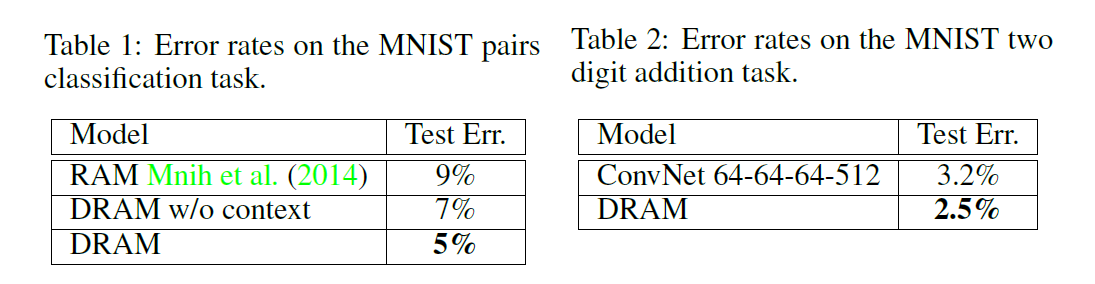
实验结果