图深度学习
基于《图深度学习》马耀,汤继良。跳过了一些专用于二分图、超图等章节。
图基础
谱图论
拉普拉斯矩阵L=D-A
定理: 对于图G={V,E},其拉普拉斯矩阵的特征值是非负的。
定理: 给定一个图G,其拉普拉斯矩阵的特征值为0的数目(特征值0的重数)等于图中连通分量的数目。
图信号的谱域基础是图傅里叶变换 (Graph Fourier Transform, GFT),它是建立在谱图论之上的。
传统的傅里叶变换可表示为:
$$
\hat{f}(\xi) = <f(t), \exp(-2\pi i \xi t)> = \int _ {-\infty}^{\infty} f(t) \exp(-2\pi i \xi t) dt
$$
式中,$ \hat{f} $ 是 $ f $ 的傅里叶变换;$ \xi $ 表示相应指数的频率。它将信号 $ f(t) $ 分解为一系列复指数形式 $ \exp(-2\pi i \xi t) $,这些指数是思维拉普拉斯算子(或二阶微分算子)的特征函数,因为:
$$
\begin{aligned} \nabla(\exp(-2\pi i \xi t)) &= \frac{\partial^2}{\partial t^2} \exp(-2\pi i \xi t) \\ &= \frac{\partial}{\partial t} (-2\pi i \xi) \exp(-2\pi i \xi t) \\ &= -(2\pi i \xi)^2 \exp(-2\pi i \xi t). \end{aligned}
$$
类似地,一个在图 $ G $ 上的信号 $ f $ 的图傅里叶变换可表示为:
$$
\hat{f}[l] = <f, u_l> = \sum _ {i=1}^{N} f[i] u_l[i]
$$
式中,$ u_l $ 表示图的拉普拉斯矩阵 $ L $ 的第 $ l $ 个特征向量,其对应的特征值 $ \lambda_l $ 表示 $ u_l $ 的频率(或平滑度)。向量 $ \hat{f} $ 是 $ f $ 的图傅里叶变换,$ \hat{f}[l] $ 表示它的第 $ l $ 个元素。这些特征向量是图 $ G $ 上傅里叶基,而 $ \hat{f} $ 由信号 $ f $ 对应这些傅里叶基的图傅里叶系数组成。$ f $ 的图傅里叶变换也可以用矩阵形式表示为:
$$
\hat{f} = U^T f
$$
式中,矩阵 $ U $ 的第 $ l $ 列是 $ u_l $。
根据
$$ u_l^T L u_l = \lambda_l \cdot u_l^T u_l = \lambda_l $$
可知特征值 $ \lambda_l $ 度量对应的特征向量 $ u_l $ 的平滑度。更具体地说,与小的特征值相关联的特征向量在图中变化缓慢,即相邻节点的特征向量的值是相似的。因此这些特征向量是平滑的,并在整个图上低频地变化。
图嵌入

node2vec:
设 $G = {V, E}$ 表示一个连通图。考虑以图 $G$ 中的 $v^{(0)} \in V$ 为起始节点的随机游走。假设随机游走规则从节点 $v^{(t-1)}$ 走到节点 $v^{(t)}$,现在停留在节点 $v^{(t)}$。接着随机游走需要决定下一步访问哪个节点。不同于 DeepWalk 中均匀地从 $v^{(t)}$ 的邻居中选择 $v^{(t+1)}$,node2vec 基于 $v^{(t)}$ 和 $v^{(t-1)}$ 定义节点的采样概率。特别地,选择下一个节点的未归一化“概率”定义如下:
$$
\alpha _ {pq}(v^{(t+1)}|v^{(t-1)}, v^{(t)}) = \begin{cases} \frac{1}{p}, & \text{dis}(v^{(t-1)}, v^{(t+1)}) = 0, \\ 1, & \text{dis}(v^{(t-1)}, v^{(t+1)}) = 1, \\ \frac{1}{q}, & \text{dis}(v^{(t-1)}, v^{(t+1)}) = 2, \end{cases}
$$
式中,$\text{dis}(v^{(t-1)}, v^{(t+1)})$ 表示节点 $v^{(t-1)}$ 和 $v^{(t+1)}$ 之间的最短路径的长度。
对于DeepWalk,有以下定理:
在矩阵形式下,给定图G,采用负采样策略的DeepWalk得到的嵌入表示等价于分解以下矩阵得到的解:
$$
log(\frac{vol(G)}{T}\sum _ {r=1}^T(AP^r)D^{-1})-log(k)
$$
其中$P=D^{-1}A$,$vol(G)=\sum _ {i=1}^|V|\sum _ {j=1}^|V A _ {i,j}$,k为负样本数量
社区模块度:
$$
Q=\frac{1}{2*vol(G)}\sum _ {ij}(A _ {i,j}-\frac{d(v_i)d(v_j)}{vol(G)})h_ih_j
$$
其中,$h_i$为节点i为哪个社区的指示值。
超图嵌入常使用MLP做辅助。
图神经网络
图滤波器
基于谱的图滤波器
使用图傅里叶变换,我们可以得到$f’=U\cdot\gamma(\Lambda)\cdot U^Tf$。
若假设有一个定义在图G上的噪声图信号$y=f_0+\eta$,其中$\eta$是附加
的与原信号不相关的高斯噪声,模型的目标是从噪声信号y中恢复原始信号$f_0$。设原始信号九相对于图G是平滑的。为了利用信号$f_0$的平滑性的先验信息,在优化问题中引入形式为$f^TLf$的正则项:
$$
argmin_f ||f-y||^2+cf^TLf
$$
求导有$f’=U(I+c\Lambda)^{-1}U^Ty$。
Poly-Filter:
对$\gamma(\cdot)$用K阶截断多项式建模,即$\gamma(\lambda_l)=\sum\theta_k\Lambda^k$。
根据$U\cdot\Lambda^k\cdot U^T=L^k$:
$$
f’=\sum \theta_k L^kf
$$
Cheby-Filter:
切比雪夫多项式$T_k(y)=2yT _ {k-1}(y)-T _ {k-2}(y)$,其中$T_0=1,,T_y=y$。
对于$y\in[-1,1]$,$T_k(y)=cos(k\cdot arccos(y))$。
此外,切比雪夫多项式满足以下关系:
$$
\int _ {-1}^{1} \frac{T_l(y)T_m(y)}{\sqrt{1-y^2}} dy =
\begin{cases}
\delta _ {l,m} \pi/2, & m, l > 0, \\
\pi, & m = l = 0,
\end{cases}
$$
因此,这些切比雪夫多项式形成了关于$dy/\sqrt{1-y^2}$的平方可积函数的希尔伯特空间(Hillbert Space)的正交基。
GCN-Filter:
将切比雪夫多项式的阶数设为K = l,并把最大特征值近似为2。即:
$$
\begin{align}
\gamma(\Lambda)&=\theta_0T_0(\tilde\Lambda)+\theta_1T_1(\tilde\Lambda)
\\&=\theta_0 I+\theta_1\tilde\Lambda
\\&=\theta_0I+\theta_1(\Lambda-I)
\end{align}
$$
用于f’时$f’=\theta_0f-\theta_1(D^{-1/2}AD^{1/2})f$,令$\theta=\theta_0=-\theta_1$,$f’=\theta(I+D^{-1/2}AD^{1/2})f$。
矩阵$I+D^{-1/2}AD^{1/2}$的特征值的范围是[0,2],故对信号f重复滤波时有可能出现数值不稳定的现象。
因此,再归一化(renormalization)技巧被提出用来解决该问题。即用$\tilde D^{-1/2}\tilde A\tilde D^{1/2}$代替$I+D^{-1/2}AD^{1/2}$,其中$\tilde A=A+I$和$\tilde D_ii=\sum_j \tilde A _ {i,j}$。经过这些简化步骤,GCN-Filter最后可被表示为:
$$
f’=\theta \tilde D^{-1/2}\tilde A\tilde D^{1/2}f
$$
基于空间的图滤波器
GraphSage-Filter
GAT-Filter
图神经网络的健壮性
简介
攻击者可以在模型训练和模型测试阶段执行攻击。根据攻击者执行攻击的能力, 攻击可大致分为逃逸攻击和投毒攻击:
- 逃逸攻击:攻击是在训练好的模型上,即在测试阶段进行的。换言之,在逃逸攻击的模式下,攻击者不能更改模型的参数或结构。
- 投毒攻击:攻击发生在模型训练之前。因此,攻击者可以在训练数据中插入“毒药”,使得基于该数据训练的模型出现故障
除节点特征外,图数据还提供了丰富的结构信息。因此,攻击者可以从不同的角度对图结构数据进行扰动,例如修改节点特征、添加或删除边和添加新节点:
- 修改节点特征:攻击者可以在保留图结构的同时修改节点的特征。
- 添加或删除边:攻击者可以添加或者删除原图中已有的边。
- 添加新节点:攻击者可以向原有的图添加新的节点,并将它们和原图中的节点相连
图对抗攻击
白盒攻击
PGD拓扑攻击:
基于积分梯度的攻击:
由于攻击者仅被允许执行从0到1或从1到0的修改,梯度信息可能没有太大帮助,因为考虑到图神经网络模型是非线性的,单个点上的梯度并不能反映诸如从0到1或从1到0的大变化的影响。因此,受积分梯度(Integrated Gradients)的启发,利用离散积分梯度来设计分数,称为积分梯度分数(IG-Score)。
$IG_H(i,j) = \sum _ {k=1}^{m} \frac{\partial \mathcal{L}_i(\frac{k}{m}(H _ {i,j} - 0))}{\partial H _ {i,j}}; \quad 1 \to 0, H _ {i,j}=1,$
$IG_H(i,j) = \sum _ {k=1}^{m} \frac{\partial \mathcal{L}_i(0 + \frac{k}{m}(1 - H _ {i,j}))}{\partial H _ {i,j}}; \quad 0 \to 1, H _ {i,j}=0$
灰盒攻击
Nettack:
$$
argmax (max\quad lnZ’ _ {i,c}-lnZ’ _ {i,y_i})
$$
其中$Z’=f _ {GNN}(A’,F’;\Theta’)$。
代理损失:
$$
L _ {sur}(A,F;\Theta,v_i)=max _ {c\ne y_i}([\tilde A^2F\Theta] _ {i,c}-[\tilde A^2F\Theta] _ {i,y_i})
$$
Metatack:
攻击者的目标可以数学地表示为一个双层优化问题:
$$
\min _ {G’ \in \Phi(G)} \mathcal{L} _ {\text{atk}}(f _ {\text{GNN}}(G’; \Theta^\ast)) \quad \text{s.t.} \quad \Theta^\ast = \arg \min _ {\Theta} \mathcal{L} _ {\text{tr}}(f _ {\text{GNN}}(G; \Theta))
$$
$f _ {GNN}$代表受害模型;tr表示用于训练模型的损失函数。
定义$L _ {atk}$的一种方法可以是将其设为训练模型的负值。另一种方法是首先使用原图g上经过良好训练的代理模型预测无标签节点的标签,然后将预测用作无标签节点的“标签”。
$$
L _ {atk}=-L _ {tr}-\beta L _ {self}
$$
使用元梯度:
$$
\begin{align}
\nabla_G^{\text{meta}} &= \nabla_G \mathcal{L} _ {\text{atk}}(f _ {\text{GNN}}(G; \Theta_T))
\\&= \nabla_f \mathcal{L} _ {\text{atk}}(f _ {\text{GNN}}(G; \Theta_T)) \cdot \left[ \nabla_G f _ {\text{GNN}}(G; \Theta_T) + \nabla _ {\Theta_T} f _ {\text{GNN}}(G; \Theta_T) \cdot \nabla_G \Theta_T \right]
\end{align}
$$
计算元梯度 $\nabla_G^{\text{meta}} = \frac{d \mathcal{L} _ {\text{atk}}}{d G}$,即攻击损失对图 $G$ 的总导数。根据链式法则,$\mathcal{L} _ {\text{atk}}$ 对 $G$ 的导数首先会涉及到 $\mathcal{L} _ {\text{atk}}$ 对 $f$ 的导数,然后再乘以 $f$ 对 $G$ 的导数:
$$ \frac{d \mathcal{L} _ {\text{atk}}}{d G} = \frac{\partial \mathcal{L} _ {\text{atk}}}{\partial f} \cdot \frac{d f}{d G} $$
$\frac{\partial \mathcal{L} _ {\text{atk}}}{\partial f}$ 即 $\nabla_f \mathcal{L} _ {\text{atk}}(f _ {\text{GNN}}(G; \Theta_T))$。由于 $f = f _ {\text{GNN}}(G, \Theta_T(G))$,其全导数为:
$$ \frac{d f}{d x} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \cdot \frac{d y}{d x} $$
反转元梯度的符号:
$$
s(i,j)=\nabla _ {A _ {i,j}}^{meta}(-2A _ {i,j}+1)
$$
黑盒攻击
在黑盒攻击设定中,攻击者无法获取受害者模型信息。攻击者只能查询受害者模型的预测结果。这类方法大多采用强化学习来学习攻击策略。它们将受害者模型视为一台黑盒查询机,利用查询结果设计强化学习的奖励。
图净化
除去特征相似度低的节点之间的边
实验研究表明,许多对抗攻击方法(如Nettack和IG-FGSM )倾向于添加边来连接节点特征明显不同的节点。类似地,当除去边时,这些攻击方法倾向于移除具有相似特征的节点之间的边。故有该方法试图除去特征差异很大的节点之间的边。更具体地说,它提出了一个评分函数度量节点特征之间的相似度。邻接矩阵的低秩近似
对Nettack等攻击产生的对抗扰动进行实验探究,结果表明,Nettack往往会扰动图结构,从而增加邻接矩阵的秩。同时,邻接矩阵取值最小的奇异值的数量也会增加。因此,有方法基于奇异值分解(SVD),以消除加入图结构中的对抗扰动。具体而言,给定一个图的邻接矩阵A,用SVD分解它, 只保留top-k个奇异值来重构邻接矩阵。重构后的邻接矩阵可以近似地认为是净化后的图结构,可直接用于图神经网络模型。
图结构学习
Pro-GNN:
$$
min _ {\Theta,S}L_train(S,F;\Theta)+||A-S||_F^2+\beta_1||S|| _ 1+\beta _ 2||S|| _ \ast+\beta _ 3\cdot tr(F^TLF)
$$
图上的其他深度模型
图上的自编码器
编码器:$Z=f _ {GNN}(A,X;\theta _ {GNN})$
解码器:$\hat A=\sigma(ZZ^T)$
图上的循环神经网络
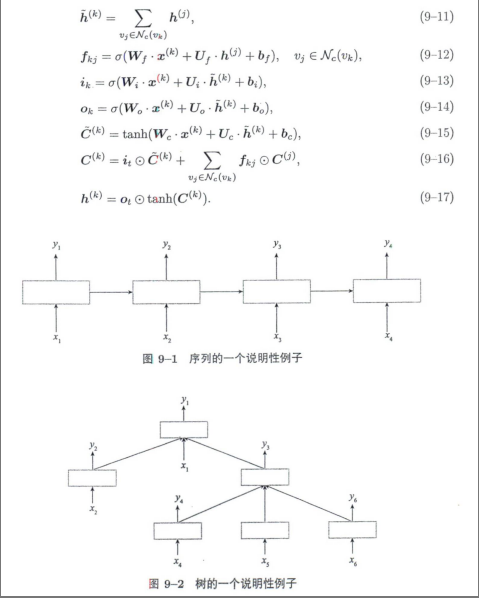
图神经网络的高级方法
定理:令G表示一个以A作为其邻接矩阵的连通的非二分图,对于任何特征$f\in R^N$,则:
$$
lim _ {L\to \infty} (D^{-\frac{1}{2}}AD^{-\frac{1}{2}})^Lf=\theta_1 u_1
$$
其中,u1是$D^{-1/2}AD^{-1/2}$与其最大特征值相关的特征向量,且$\theta_1 u_1^T f$
WL测试
定理:给定任意两个非同构图G1和G2,如果图神经网络模型将这两个图映射到不同的嵌入中,则WL测试也可以确定这两个图是非同构的。
定理:如果图神经网络模型中的AGG()、COM()和POOL()函数是单射的,当它有足够多的图滤波层时,可以将通过WL测试为非同构的两个图映射到不同的嵌入。