高斯混合模型和EM算法

Tabular Playground Series - Jul 2022是一场无监督聚类比赛，第一名采用了不到一百行代码，主要核心内容是使用GMM和EM。

模型定义

假设观测数据集为 ${x_1, x_2, \dots, x_N}$，每个 $x_i\in\mathbb{R}^D$。GMM 假设数据的生成过程为：

1. 从 $K$ 个高斯分布中，以概率 $\pi_k$ 选取第 $k$ 个分量，其中
   $$
   \sum_{k=1}^K \pi_k = 1,\quad \pi_k\ge0.
   $$
2. 给定选中的组件 $k$，从第 $k$ 个高斯分布中采样：
   $$
   x_i \sim \mathcal{N}(x\mid\mu_k,\Sigma_k).
   $$

因此，对任意一个观测 $x$ 的似然为：
$$
p(x\mid {\pi_k,\mu_k,\Sigma_k}_ {k=1}^K)
= \sum_ {k=1}^K \pi_k,\mathcal{N}(x\mid\mu_k,\Sigma_k).
$$

目标：最大化对数似然

我们希望找到参数集合 $\Theta={\pi_k,\mu_k,\Sigma_k}_ {k=1}^K$，使得观测数据的对数似然最大：
$$
\mathcal{L}(\Theta)=ln\prod_{i=1}^N \sum _ {k=1}^K \pi _ k,\mathcal{N}(x _ i \mid \mu _ k,\Sigma _ k) = \sum _ {i=1}^N ln(\sum _ {k=1}^K \pi _ k,\mathcal{N}(x_i \mid \mu_k,\Sigma _ k))
$$
直接对上式求导并解出闭式解困难，因此引入 EM 算法来迭代优化。

EM 算法概览

EM 算法将“数据点属于哪个组件”视作隐变量 $z_i$，其中 $z_i=k$ 表示第 $i$ 个点来自第 $k$ 个高斯分量。算法在每次迭代中分两步：

1. E 步（Expectation）
   计算当前参数下，各数据点属于各分量的“后验概率”——责任度（responsibility）
   $$
   \gamma_{ik}
   = p(z_i = k \mid x_i,,\Theta^{\text{old}})
   = \frac{\pi_k^{\text{old}};\mathcal{N}(x_i\mid\mu_k^{\text{old}},\Sigma_k^{\text{old}})}
   {\sum_{j=1}^K \pi_j^{\text{old}};\mathcal{N}(x_i\mid\mu_j^{\text{old}},\Sigma_j^{\text{old}})}.
   $$

2. M 步（Maximization）
   利用上面算得的 $\gamma_{ik}$ 来更新参数，使得期望完全数据对数似然最大：

   • 有效样本数：
     $$
     N_k = \sum_{i=1}^N \gamma_{ik}.
     $$
   • 更新混合权重：
     $$
     \pi_k^{\text{new}} = \frac{N_k}{N}.
     $$
   • 更新均值：
     $$
     \mu_k^{\text{new}}
     = \frac{1}{N_k} \sum_{i=1}^N \gamma_{ik},x_i.
     $$
   • 更新协方差：
     $$
     \Sigma_k^{\text{new}}
     = \frac{1}{N_k} \sum_{i=1}^N \gamma_{ik},(x_i - \mu_k^{\text{new}})(x_i - \mu_k^{\text{new}})^\top.
     $$

不断迭代 E 步和 M 步，直到参数收敛（对数似然增益低于阈值或达到最大迭代次数）。

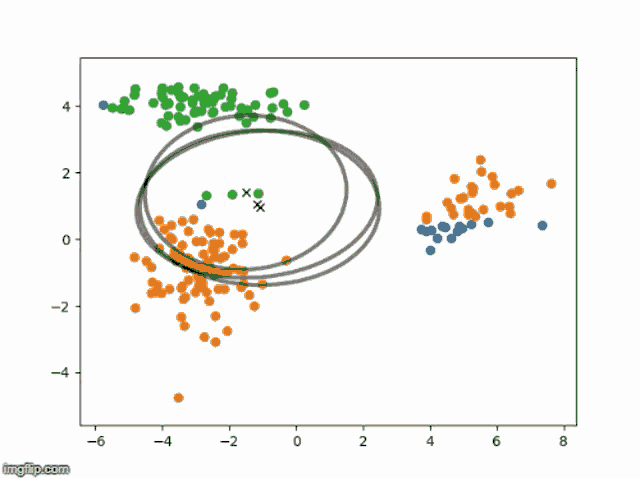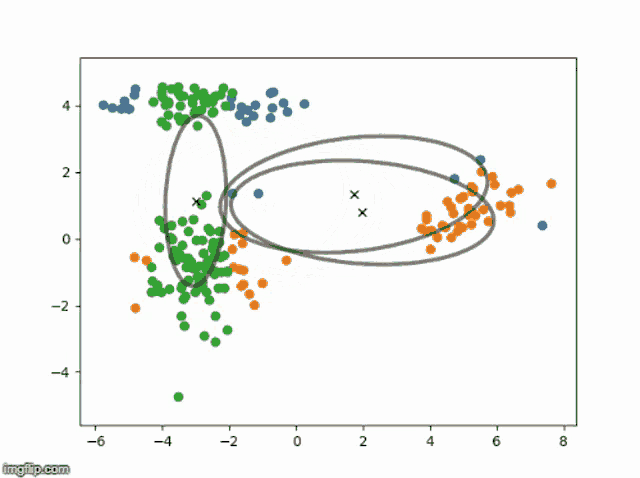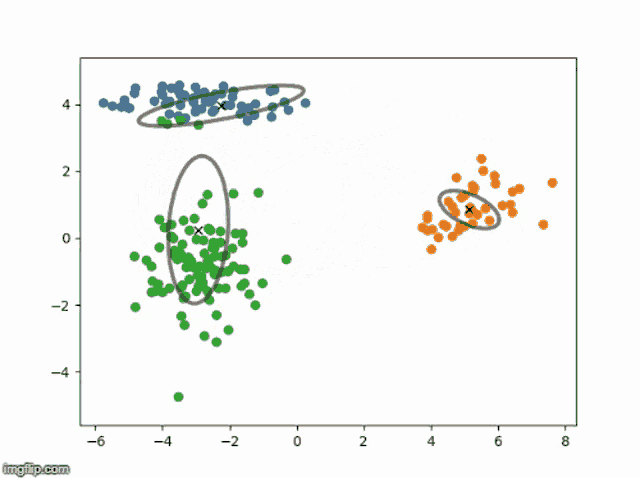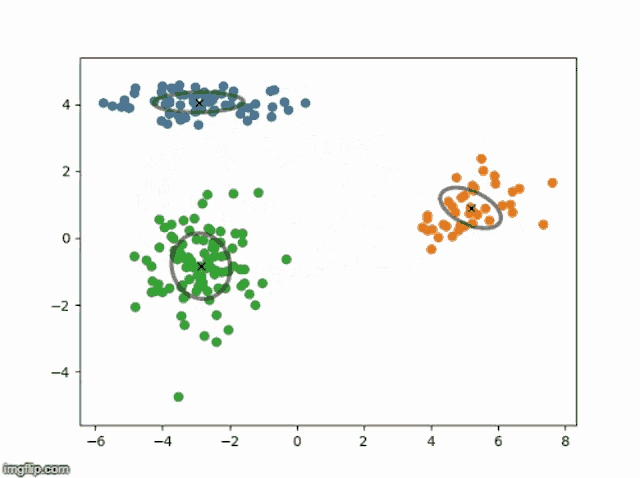
EM 算法伪代码

输入：数据 X={x₁,…,xₙ}，组件数 K，收敛阈值 ε，最大迭代 T
初始化：随机或用 K-Means 给出 {πₖ, μₖ, Σₖ}

for t = 1 to T:
  — E 步 —
  对 i=1…N, k=1…K 计算责任度 γᵢₖ

  — M 步 —
  对 k=1…K 计算 Nₖ = ∑ᵢ γᵢₖ
  更新：
    πₖ ← Nₖ / N
    μₖ ← (1/Nₖ) ∑ᵢ γᵢₖ xᵢ
    Σₖ ← (1/Nₖ) ∑ᵢ γᵢₖ (xᵢ − μₖ)(xᵢ − μₖ)ᵀ

  计算对数似然 Lᵗ
  如果 |Lᵗ − Lᵗ⁻¹| < ε: 退出

返回：{πₖ, μₖ, Σₖ}ₖ₌₁…K

和kmeans关系

考虑一个GMM，$\epsilon$是被所有分量共享的方差参数。
$$
P(x|\mu_k,\Sigma_k)=\frac{1}{(2\pi \epsilon)^{D/2}}exp(-\frac{1}{2\epsilon}||x-\mu_K||)
$$
我们把$\epsilon$看作一个固定的常数，则责任度为：
$$
\frac{\pi_k exp(-\frac{||x_n-\mu_k||^2}{2\epsilon})}
{\sum_{j=1}^K \pi_j exp(-\frac{||x_n-\mu_j||^2}{2\epsilon})}.
$$
当我们考虑$\epsilon \to0$，则项j责任度趋向于趋向于1，其他趋向于0。相当于对数据点聚类的硬分配。

进一步的$\epsilon \to0$时，对数似然函数为：

$-\frac{1}{2}\sum_{n=1}^N\sum_{k=1}^K r_{nk}||x_n-\mu_k||^2$

参考资料

PRML

https://www.kaggle.com/competitions/tabular-playground-series-jul-2022/discussion/334887