暗通道先验去雾

暗通道去雾由何恺明提出，其基于一个观察：在绝大多数户外无雾图像的非天空区域，至少有一个颜色通道的强度值非常低，趋近于零。这个“非常低的强度值”就是所谓的“暗像素”，而由这些暗像素构成的图像就是“暗通道”。

算法

暗通道去雾算法主要包含以下几个关键步骤：

计算暗通道图像 (Compute Dark Channel):
- 对于输入图像的每一个像素，在一个局部窗口内（例如15x15），分别找出其R、G、B三个通道的最小值。
- 然后，再在这些最小值中找出最小的那个值，作为该像素在暗通道图像中的值。
- 用公式表达就是：
  $J^{dark}(x) = \min_{y \in \Omega(x)} (\min_{c \in {r,g,b}} J^c(y))$
  其中，$J^c$ 是彩色图像的一个颜色通道，$Ω(x)$ 是以像素 $x$ 为中心的局部块。
估计大气光照 (Estimate Atmospheric Light):
- 大气光 $A$ 通常是图像中最亮的部分，也即雾最浓的区域。
- 在暗通道图像中，选取最亮的一定比例（例如0.1%）的像素。
- 在原始有雾图像中，找到这些对应位置的像素，并取这些像素的平均值或最大值作为大气光 $A$ 的估计值。
估计透射率 (Estimate Transmission Map):
- 大气散射模型可以简化为： $I(x) = J(x)t(x) + A(1-t(x))$
  - $I(x)$ 是我们观察到的有雾图像。
  - $J(x)$ 是我们想要恢复的无雾图像。
  - $A$ 是全局大气光。
  - $t(x)$ 是透射率，表示光线从场景点到达相机过程中没有被散射的比例。$t(x)$ 的值越小，表示雾越浓。
- 根据暗通道先验，$J^{dark}(x) \approx 0$。将这个先验代入到归一化后的大气散射模型中（即各项除以 $A$），可以得到透射率的估计。更准确地，原文中是对 $I(x)/A$ 求暗通道来估计透射率：
  $t(x) \approx 1 - \omega \cdot\frac{J^{dark}(x)}{A^c}$
  其中，$A^c$ 是大气光 $A$ 对应通道的强度值。$\omega$ 是一个修正系数（通常取0.95），用于保留少量远景的雾，使图像看起来更自然。
- 这个初步得到的透射率图通常是块状的，需要进行精细化处理。
精细化透射率图 (Refine Transmission Map):

为了得到更精确的透射率图，通常会使用软抠图 (Soft Matting) 或者导向滤波 (Guided Filter) 等方法对初始透射率图进行平滑和边缘保持处理。导向滤波因其高效性和良好的效果而被广泛使用。

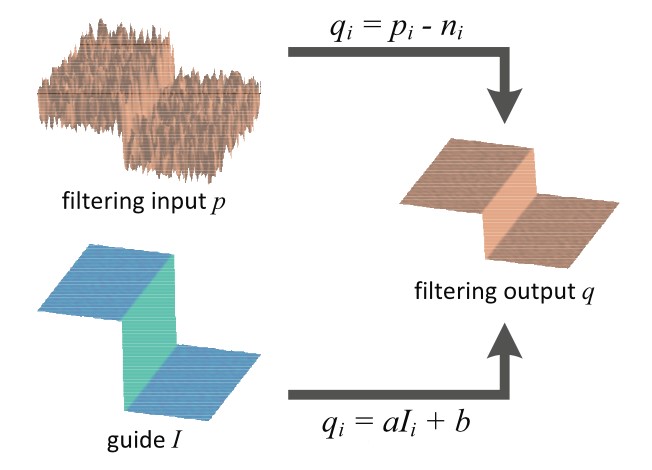
导向滤波，即参考另一张图像（称之为“引导图像”）的结构信息对一张图像进行平滑处理。引导图像“告诉”滤波器哪里是边缘，哪里是平坦区域。当滤波器处理输入图像时，如果引导图像在某个位置显示有边缘，滤波器就会努力保持输入图像在该位置的边缘；如果引导图像显示为平坦区域，滤波器就会对输入图像的相应区域进行更强的平滑。
恢复无雾图像 (Recover Scene Radiance):
- 有了大气光 $A$ 和精细化的透射率图 $t(x)$，就可以根据大气散射模型反解出无雾图像 $J(x)$：
  $J(x) = \frac{I(x) - A}{t(x)} + A$
- 为了防止当 $t(x)$ 值过小时除数过小导致结果不稳定，通常会设定一个透射率的下限 $t_0$ (例如0.1)：
  $J(x) = \frac{I(x) - A}{\max(t(x), t_0)} + A$